Infinitesimale Weg-, Flächen-, und Volumenelemente: Unterschied zwischen den Versionen
| (207 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Navigation|before=[[Differentialquotient]]|overview=[[Infinitesimale Weg-, Flächen-, und Volumenelemente]]|next=[[Wegelemente]]}} | |
| + | {{Aufgabe|Selbsttest:Infinitesimale_Weg-,_Flächen-_und_Volumenelemente}} | ||
| + | ==Einführung== | ||
| + | Infinitesimale (von lateinisch ''infinitus'' = unbegrenzt, hier sinngemäß: beliebig/unbegrenzt klein) Weg-, Flächen-, und Volumenelemente spielen eine zentrale Rolle in der [[Differentialquotient|Differential-]] und Integralrechnung. So treten in der Lehrveranstaltung zum Beispiel verschiedene [[Erweiterung der Integralrechnung:Übersicht|vektorielle Mehrfachintegrale]] auf, in denen diese Elemente verwendet werden. | ||
| − | :<math>\ | + | Die Spannung <math>U_{12}</math> zwischen zwei Punkten <math>P_1</math> und <math>P_2</math> in einem elektrischen Feld <math>\vec{\textbf{E}}</math> lässt sich unter anderem wie folgt bestimmen: |
| + | :<math> | ||
| + | U_{12} = \int_{P_1}^{P_2} \vec{\textbf{E}} \cdot \mathrm{d}\vec{\textbf{s}} | ||
| + | </math> | ||
| + | In diesem Fall wird über eine beliebige Kontur, die am Punkt <math>P_1</math> beginnt und am Punkt <math>P_2</math> endet, integriert. Dabei beschreibt <math>\mathrm{d}\vec{\textbf{s}}</math> ein '''infinitesimales''' (d. h. beliebig kleines) '''gerichtetes Teilstück''' (gerichtet da vektoriell) dieser Kontur (siehe auch [[Das Linienintegral|Linienintegral]]). Der Ausdruck <math>\mathrm{d}\vec{\textbf{s}}</math> wird '''Differential''' genannt und entsprechend spricht man auch von einer '''differentiellen Wegänderung'''. | ||
| − | + | Die nachfolgende Übersicht zeigt typische Varianten von infinitesimalen Elementen, die auf Artikel mit ausführlicheren Erklärungen und Beispielen verweisen. Eine Übersicht verschiedener Elemente in verschiedenen [[Orthogonale Koordinatensysteme:Übersicht|Koordinatensystemen]] findet sich in der [[Formelsammlung Koordinatensysteme]]. | |
| − | + | ==Übersicht== | |
| + | {| cellpadding="10" | ||
| + | |- | ||
| + | |style="background-color:#dde6f3;"|[[Wegelemente]] | ||
| + | Infinitesimale Wegelemente (d. h. beliebig kleine Teilelemente einer Kontur, die meist mit <math>C</math> bezeichnet wird) werden zum Beispiel im Zusammenhang mit [[Das Linienintegral|Linienintegralen]] benötigt. Die Elemente werden meist mit <math>\mathrm{d}s</math> beziehungsweise bei einer gerichteten Kontur mit <math>\mathrm{d}\vec{\textbf{s}}</math> bezeichnet. Die Richtung in einem bestimmten Punkt der Kontur entspricht dabei derjenigen einer in diesem Punkt angelegten Tangente. | ||
| − | + | |style="background-color:#c9d7ec;"|[[Image:Linienladung_Gerade.svg|220px|miniatur|center]] | |
| − | + | |- | |
| − | + | |style="background-color:#dde6f3"|[[Flächenelemente]] | |
| + | Infinitesimale Flächenelemente (d. h. beliebig kleine Teilelemente einer Fläche, die meist mit <math>A</math> bezeichnet wird) werden zum Beispiel im Zusammenhang mit [[Das Flächenintegral|Flächenintegralen]] benötigt. Die Elemente werden meist mit <math>\mathrm{d}A</math> beziehungsweise bei einer gerichteten Fläche mit <math>\mathrm{d}\vec{\textbf{A}}</math> bezeichnet. Die Richtung eines bestimmten Teilelements der Fläche entspricht dabei einem darauf senkrecht stehenden Einheitsvektor (=Flächennormalenvektor oder kurz '''Normalenvektor'''). | ||
| − | + | |style="background-color:#c9d7ec;"|[[Image:Flaechenelement.svg|220px|miniatur|center]] | |
| + | |- | ||
| + | |style="background-color:#dde6f3"|[[Volumenelemente]] | ||
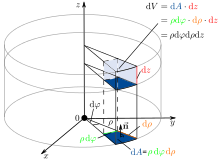
| + | Infinitesimale Volumenelemente (d. h. beliebig kleine Teilelemente eines Volumens, das meist mit <math>V</math> bezeichnet wird) werden zum Beispiel im Zusammenhang mit [[Das Volumenintegral|Volumenintegralen]] benötigt. Die Elemente werden meist mit <math>\mathrm{d}V</math> bezeichnet. Da einem Volumen keine Richtung zugeordnet werden kann, tritt dieses Element immer nur als Betrag auf. | ||
| + | |style="background-color:#c9d7ec;"|[[Image:Volumenelement Zylinder.svg|220px|miniatur|center]] | ||
| + | |} | ||
| − | + | === Video zu den Elementen in verschiedenen Koordinatensystemen === | |
| − | + | <youtube width="560" height="315">7VMsSM5mAX0</youtube> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<noinclude>==Literatur== | <noinclude>==Literatur== | ||
* Manfred Albach, ''Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen'', 3. Auflage (Pearson Studium, 2011) | * Manfred Albach, ''Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen'', 3. Auflage (Pearson Studium, 2011) | ||
| − | * Kurt Meyberg | + | * Kurt Meyberg und Peter Vachenauer, ''Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung'', 6. Auflage (Springer Berlin Heidelberg, 2001) |
| − | * Klaus Jänich Mathematik 1 Geschrieben für Physiker,2. Auflage (Springer Berlin Heidelberg, 2005) | + | * Klaus Jänich, ''Mathematik 1 Geschrieben für Physiker'', 2. Auflage (Springer Berlin Heidelberg, 2005) |
| − | * Wolfgang Pavel | + | * Wolfgang Pavel und Ralf Winkler, ''Mathematik für Naturwissenschaftler'', 1. Auflage (Pearson Studium, 2007) |
| − | * Dr. Hempel, | + | * Dr. Thomas Hempel, ''Mathematische Grundlagen'', Linienintegral, Vorlesungsskript, Universität Magdeburg, 2010 |
| − | + | </noinclude> | |
| − | + | [[Kategorie:Artikel]] | |
| − | + | [[Kategorie:Feedback]] | |
Aktuelle Version vom 4. Dezember 2018, 19:58 Uhr
| ← Zurück: Differentialquotient | Übersicht: Infinitesimale Weg-, Flächen-, und Volumenelemente | Vorwärts: Wegelemente → |
|
Zu diesem Thema stehen Aufgaben zur Selbstkontrolle zur Verfügung. |
Inhaltsverzeichnis
Einführung
Infinitesimale (von lateinisch infinitus = unbegrenzt, hier sinngemäß: beliebig/unbegrenzt klein) Weg-, Flächen-, und Volumenelemente spielen eine zentrale Rolle in der Differential- und Integralrechnung. So treten in der Lehrveranstaltung zum Beispiel verschiedene vektorielle Mehrfachintegrale auf, in denen diese Elemente verwendet werden.
Die Spannung 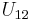 zwischen zwei Punkten
zwischen zwei Punkten 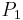 und
und 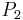 in einem elektrischen Feld
in einem elektrischen Feld 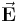 lässt sich unter anderem wie folgt bestimmen:
lässt sich unter anderem wie folgt bestimmen:
In diesem Fall wird über eine beliebige Kontur, die am Punkt 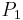 beginnt und am Punkt
beginnt und am Punkt 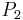 endet, integriert. Dabei beschreibt
endet, integriert. Dabei beschreibt 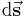 ein infinitesimales (d. h. beliebig kleines) gerichtetes Teilstück (gerichtet da vektoriell) dieser Kontur (siehe auch Linienintegral). Der Ausdruck
ein infinitesimales (d. h. beliebig kleines) gerichtetes Teilstück (gerichtet da vektoriell) dieser Kontur (siehe auch Linienintegral). Der Ausdruck 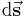 wird Differential genannt und entsprechend spricht man auch von einer differentiellen Wegänderung.
wird Differential genannt und entsprechend spricht man auch von einer differentiellen Wegänderung.
Die nachfolgende Übersicht zeigt typische Varianten von infinitesimalen Elementen, die auf Artikel mit ausführlicheren Erklärungen und Beispielen verweisen. Eine Übersicht verschiedener Elemente in verschiedenen Koordinatensystemen findet sich in der Formelsammlung Koordinatensysteme.
Übersicht
| Wegelemente
Infinitesimale Wegelemente (d. h. beliebig kleine Teilelemente einer Kontur, die meist mit |
|
| Flächenelemente
Infinitesimale Flächenelemente (d. h. beliebig kleine Teilelemente einer Fläche, die meist mit |
|
| Volumenelemente
Infinitesimale Volumenelemente (d. h. beliebig kleine Teilelemente eines Volumens, das meist mit |
Video zu den Elementen in verschiedenen Koordinatensystemen
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Klaus Jänich, Mathematik 1 Geschrieben für Physiker, 2. Auflage (Springer Berlin Heidelberg, 2005)
- Wolfgang Pavel und Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Thomas Hempel, Mathematische Grundlagen, Linienintegral, Vorlesungsskript, Universität Magdeburg, 2010
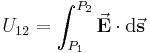
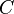 bezeichnet wird) werden zum Beispiel im Zusammenhang mit
bezeichnet wird) werden zum Beispiel im Zusammenhang mit 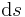 beziehungsweise bei einer gerichteten Kontur mit
beziehungsweise bei einer gerichteten Kontur mit 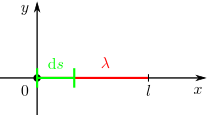
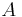 bezeichnet wird) werden zum Beispiel im Zusammenhang mit
bezeichnet wird) werden zum Beispiel im Zusammenhang mit 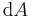 beziehungsweise bei einer gerichteten Fläche mit
beziehungsweise bei einer gerichteten Fläche mit 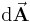 bezeichnet. Die Richtung eines bestimmten Teilelements der Fläche entspricht dabei einem darauf senkrecht stehenden Einheitsvektor (=Flächennormalenvektor oder kurz Normalenvektor).
bezeichnet. Die Richtung eines bestimmten Teilelements der Fläche entspricht dabei einem darauf senkrecht stehenden Einheitsvektor (=Flächennormalenvektor oder kurz Normalenvektor).

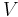 bezeichnet wird) werden zum Beispiel im Zusammenhang mit
bezeichnet wird) werden zum Beispiel im Zusammenhang mit 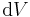 bezeichnet. Da einem Volumen keine Richtung zugeordnet werden kann, tritt dieses Element immer nur als Betrag auf.
bezeichnet. Da einem Volumen keine Richtung zugeordnet werden kann, tritt dieses Element immer nur als Betrag auf.