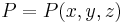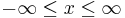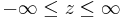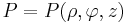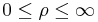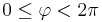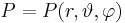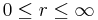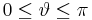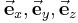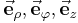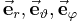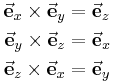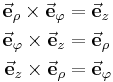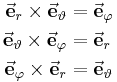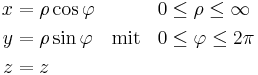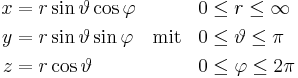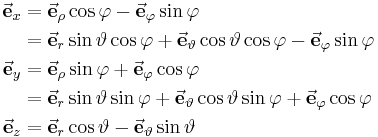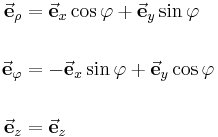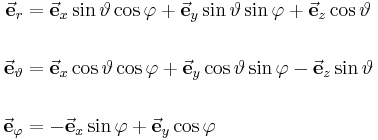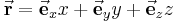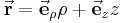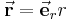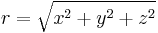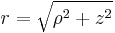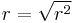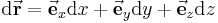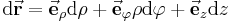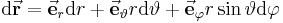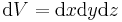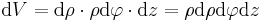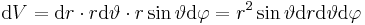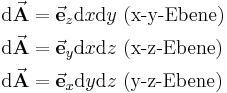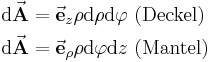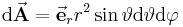Formelsammlung Koordinatensysteme

	Kartesische Koordinaten	Zylinderkoordinaten	Kugelkoordinaten

Wertebereiche der Koordinaten	$P=P(x,y,z)$ $-\infty\leq x\leq\infty$ $-\infty\leq y\leq\infty$ $-\infty\leq z\leq\infty$	$P=P(\rho,\varphi,z)$ $0 \leq \rho \leq\infty$ $0 \leq \varphi < 2\pi$ $-\infty \leq z \leq\infty$	$P=P(r,\vartheta,\varphi)$ $0\leq r\leq\infty$ $0\leq \vartheta\leq\pi$ $0\leq \varphi < 2\pi$
Einheitsvektoren	$\vec{\mathbf{e}}_x,\vec{\mathbf{e}}_y,\vec{\mathbf{e}}_z$	$\vec{\mathbf{e}}_{\rho},\vec{\mathbf{e}}_{\varphi},\vec{\mathbf{e}}_z$	$\vec{\mathbf{e}}_r, \vec{\mathbf{e}}_{\vartheta},\vec{\mathbf{e}}_{\varphi}$
Kreuzprodukt	$\begin{align} \vec{\mathbf{e}}_x\times\vec{\mathbf{e}}_y &=\vec{\mathbf{e}}_z\\ \vec{\mathbf{e}}_y\times\vec{\mathbf{e}}_z &=\vec{\mathbf{e}}_x\\ \vec{\mathbf{e}}_z\times\vec{\mathbf{e}}_x &=\vec{\mathbf{e}}_y \end{align}$	$\begin{align} \vec{\mathbf{e}}_{\rho}\times\vec{\mathbf{e}}_{\varphi} &=\vec{\mathbf{e}}_z\\ \vec{\mathbf{e}}_{\varphi}\times\vec{\mathbf{e}}_z &=\vec{\mathbf{e}}_{\rho}\\ \vec{\mathbf{e}}_z \times\vec{\mathbf{e}}_{\rho} &=\vec{\mathbf{e}}_{\varphi} \end{align}$	$\begin{align} \vec{\mathbf{e}}_r\times\vec{\mathbf{e}}_{\vartheta} &= \vec{\mathbf{e}}_{\varphi}\\ \vec{\mathbf{e}}_{\vartheta}\times\vec{\mathbf{e}}_{\varphi} &= \vec{\mathbf{e}}_r\\ \vec{\mathbf{e}}_{\varphi}\times\vec{\mathbf{e}}_r &= \vec{\mathbf{e}}_{\vartheta} \end{align}$
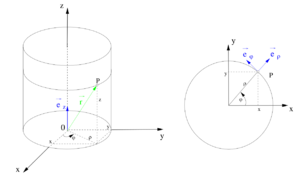
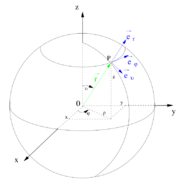
Zusammenhang zu kartesischen Koordinaten		$\begin{align} x &=\rho\cos{\varphi} && && 0\leq\rho\leq\infty\\ y &=\rho\sin{\varphi} &&\text{mit}&& 0\leq\varphi\leq2\pi\\ z &=z \end{align}$	$\begin{align}x &=r\sin{\vartheta}\cos{\varphi} && && 0\leq r \leq\infty\\ y &=r\sin{\vartheta}\sin{\varphi} &&\text{mit}&& 0\leq\vartheta\leq \pi\\ z &=r\cos{\vartheta} && && 0\leq\varphi\leq 2\pi \end{align}$
Umrechnungen	$\begin{align} \vec{\mathbf{e}}_x &= \vec{\mathbf{e}}_{\rho}\cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\ &= \vec{\mathbf{e}}_r\sin{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_{\vartheta} \cos{\vartheta} \cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\ \vec{\mathbf{e}}_y &= \vec{\mathbf{e}}_{\rho}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\ &= \vec{\mathbf{e}}_r\sin{\vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\vartheta}\cos{\vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\ \vec{\mathbf{e}}_z &= \vec{\mathbf{e}}_r\cos{\vartheta}-\vec{\mathbf{e}}_{\vartheta}\sin{\vartheta}\\ \end{align}$	$\begin{align}\vec{\mathbf{e}}_{\rho} &= \vec{\mathbf{e}}_x\cos{\varphi}+\vec{\mathbf{e}}_y\sin{\varphi}\\ \\ \vec{\mathbf{e}}_{\varphi} &= -\vec{\mathbf{e}}_x\sin{\varphi}+\vec{\mathbf{e}}_y\cos{\varphi}\\ \\ \vec{\mathbf{e}}_z &= \vec{\mathbf{e}}_z \end{align}$	$\begin{align}\vec{\mathbf{e}}_r &= \vec{\mathbf{e}}_x\sin{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_y\sin{\vartheta} \sin{\varphi}+\vec{\mathbf{e}}_z\cos{\vartheta}\\ \\ \vec{\mathbf{e}}_{\vartheta} &= \vec{\mathbf{e}}_x\cos{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_y\cos{\vartheta}\sin{\varphi}-\vec{\mathbf{e}}_z\sin{\vartheta}\\ \\ \vec{\mathbf{e}}_{\varphi} &= -\vec{\mathbf{e}}_x\sin{\varphi}+\vec{\mathbf{e}}_y\cos{\varphi} \end{align}$
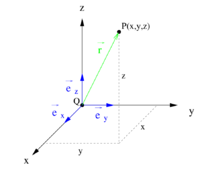
Ortsvektor	$\vec{\mathbf{r}}=\vec{\mathbf{e}}_x x+\vec{\mathbf{e}}_y y+\vec{\mathbf{e}}_z z$	$\vec{\mathbf{r}}=\vec{\mathbf{e}}_{\rho}\rho+\vec{\mathbf{e}}_z z$	$\vec{\mathbf{r}}=\vec{\mathbf{e}}_r r$
Betrag des Ortsvektors	$r=\sqrt{x^2+y^2+z^2}$	$r=\sqrt{\rho^2+z^2}$	$r=\sqrt{r^2}$
vektorielles Wegelement	$\mathrm{d}\vec{\mathbf{r}}=\vec{\mathbf{e}}_x\mathrm{d}x+\vec{\mathbf{e}}_y\mathrm{d}y+\vec{\mathbf{e}}_z\mathrm{d}z$	$\mathrm{d}\vec{\mathbf{r}}=\vec{\mathbf{e}}_{\rho}\mathrm{d}\rho+\vec{\mathbf{e}}_{\varphi}\rho\mathrm{d}\varphi+\vec{\mathbf{e}}_z\mathrm{d}z$	$\mathrm{d}\vec{\mathbf{r}}=\vec{\mathbf{e}}_r\mathrm{d}r+\vec{\mathbf{e}}_{\vartheta}r\mathrm{d}\vartheta+\vec{\mathbf{e}}_{\varphi}r\sin\vartheta\mathrm{d}\varphi$
Volumenelement	$\mathrm{d}V=\mathrm{d}x\mathrm{d}y\mathrm{d}z$	$\mathrm{d}V=\mathrm{d}\rho\cdot\rho\mathrm{d}\varphi\cdot\mathrm{d}z=\rho\mathrm{d}\rho\mathrm{d}\varphi\mathrm{d}z$	$\mathrm{d}V=\mathrm{d}r\cdot r\mathrm{d}\vartheta\cdot r\sin\vartheta\mathrm{d}\varphi=r^2\sin\vartheta\mathrm{d}r\mathrm{d}\vartheta\mathrm{d}\varphi$
vektorielles Flächenelement	$\begin{align} \mathrm{d}\vec{\mathbf{A}} &= \vec{\mathbf{e}}_z\mathrm{d}x\mathrm{d}y \text{ (x-y-Ebene)}\\ \mathrm{d}\vec{\mathbf{A}} &= \vec{\mathbf{e}}_y\mathrm{d}x\mathrm{d}z \text{ (x-z-Ebene)}\\ \mathrm{d}\vec{\mathbf{A}} &= \vec{\mathbf{e}}_x\mathrm{d}y\mathrm{d}z \text{ (y-z-Ebene)} \end{align}$	$\begin{align} \mathrm{d}\vec{\mathbf{A}} &= \vec{\mathbf{e}}_z\rho\mathrm{d}\rho\mathrm{d}\varphi \text{ (Deckel)}\\ \mathrm{d}\vec{\mathbf{A}} &= \vec{\mathbf{e}}_\rho\rho\mathrm{d}\varphi\mathrm{d}z \text{ (Mantel)} \end{align}$	$\mathrm{d}\vec{\mathbf{A}}=\vec{\mathbf{e}}_r r^2\sin\vartheta\mathrm{d}\vartheta\mathrm{d}\varphi$