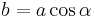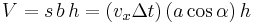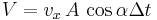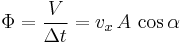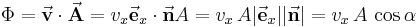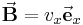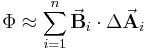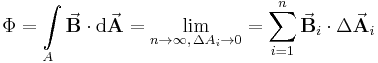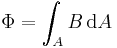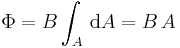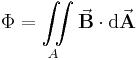Das Flächenintegral

← Zurück: Das Linienintegral

Übersicht: Erweiterung der Integralrechnung

Vorwärts: Das Volumenintegral →

Das Flächen- oder Oberflächenintegral beschreibt eine Integration über eine (gerichtete) Fläche. Da in diesem Fall eine Schachtelung von zwei Integrationsintervallen betrachtet wird, gibt es auch zwei Integrationsvariablen. Handelt es sich zum Beispiel um eine Fläche in der 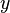$x$-$y$-Ebene eines kartesischen Koordinatensystems, so ist das Differential durch 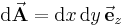$\mathrm{d}\vec{\textbf{A}} = \mathrm{d}x\,\mathrm{d}y\,\vec{\textbf{e}}_z$ gegeben (Flächennormale zeigt hier in Richtung 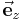$\vec{\textbf{e}}_z$). Handelt es sich um eine geschlossene Fläche (= Hüllfläche), so wird das Integral als Hüllflächenintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.

Fluss durch eine ebene Fläche

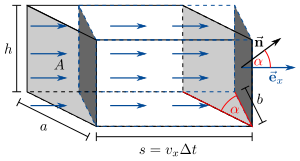
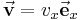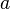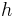Zur Verdeutlichung der Bedeutung des Flächenintegrals wird ein physikalisches Beispiel herangezogen. Betrachtet wird eine Flüssigkeit, die sich homogen und mit einer konstanten Geschwindigkeit $\vec{\textbf{v}} = v_x \vec{\textbf{e}}_x$ durch eine Ebene Fläche bewegt (siehe Abbildung). Die Fläche ist dabei durch ein Rechteck mit den Kantenlängen $a$ und $h$ gegeben, welches im Winkel 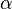$\alpha$ (siehe Flächennormale 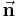$\vec{\textbf{n}}$) zur Bewegungsrichtung der Flüssigkeit steht. Es soll nun die Frage beantwortet werden, wie viel Flüssigkeit 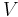$V$ pro Zeitintervall durch die Fläche strömt.

Zunächst lässt sich festhalten, dass die Flüssigkeit in einem Zeitintervall 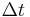$\Delta t$ die Strecke 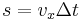$s=v_x \Delta t$ (Geschwindigkeit=Strecke/Zeit, dieser Zusammenhang muss lediglich umgestellt werden) zurücklegt. Platziert man weiterhin eine Fläche senkrecht zur Bewegungsrichtung der Flüssigkeit, die im Vergleich zur gekippten Fläche den gleichen Bereich abdeckt, so lässt sich folgender Zusammenhang feststellen: Durch die senkrechte Fläche tritt die gleiche Menge an Flüssigkeit wie durch die gekippte Fläche. 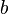Damit entspricht die Flüssigkeitsmenge, die durch diese Flächen tritt, dem Volumen des Quaders mit den Grundseiten $s$ und $b$ sowie der Höhe 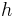$h$ (vgl. Abbildung). Für die Länge der Grundseite 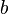$b$ folgt mit Hilfe trigonometrischer Funktionen:

$b = a\cos\alpha$

Damit folgt für die Flüssigkeitsmenge:

$V = s\,b\,h = (v_x \Delta t)\,(a\cos\alpha)\,h$

In dieser Gleichung entspricht 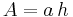$A=a\,h$ dem Flächeninhalt der gekippten Fläche, daher gilt:

$V = v_x\,A\,\cos\alpha\Delta t$

Die Flüssigkeitsmenge 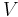$V$, die pro Zeitintervall 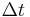$\Delta t$ durch die Fläche tritt, wird als Fluss 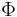$\Phi$ bezeichnet:

$\Phi = \frac{V}{\Delta t} = v_x\,A\,\cos\alpha$

Die in der Gleichung vorkommende Kosinus-Funktion lässt bereits auf einen Zusammenhang zum Skalarprodukt schließen. Damit lässt sich die Gleichung nämlich auch wie folgt formulieren:

$\Phi = \vec{\textbf{v}}\cdot\vec{\textbf{A}} = v_x \vec{\textbf{e}}_x \cdot \vec{\textbf{n}} A = v_x\,A |\vec{\textbf{e}}_x ||\vec{\textbf{n}}| = v_x\,A\,\cos\alpha$

Der Fluss entspricht damit der Flüssigkeitsmenge, die in einem Zeitintervall durch die gesamte Fläche tritt. Um eine von der Größe der Fläche unabhängige Größe zu erhalten, wird die Flussdichte 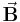$\vec{\textbf{B}}$ (Fluss pro Fläche) eingeführt:

$\vec{\textbf{B}} = v_x \vec{\textbf{e}}_x$

Fluss durch eine gekrümmte Fläche

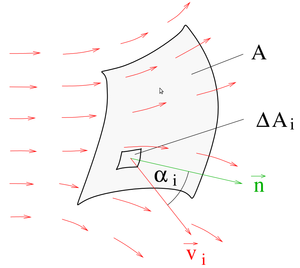
Im allgemeinen Fall hat man es nicht mit einer ortsunabhängigen (konstanten) Fließgeschwindigkeit zu tun. Weiterhin können die betrachteten Flächen beliebige Formen annehmen (siehe Abbildung).

Möchte man in diesem Fall den Fluss bestimmen, so muss die ortsabhängige Flussdichte über die Fläche aufsummiert (integriert) werden. Dazu kann diese zunächst in 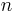$n$ sehr kleine Teilstücke zerlegt werden, wobei das 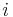$i$-te Teilstück mit 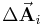$\Delta \vec{\textbf{A}}_i$ bezeichnet wird. Damit kann jedem Teilstück eine näherungsweise konstante Flächennormale 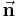$\vec{\textbf{n}}$ sowie eine näherungsweise konstante Flussdichte 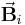$\vec{\textbf{B}}_i$ zugeordnet werden. Die Flächennormale gibt dabei vor, in welche Richtung der Fluss positiv zu zählen ist. Somit folgt:

$\Phi \approx \sum_{i=1}^n \vec{\textbf{B}}_i\cdot\Delta\vec{\textbf{A}}_i$

Die Näherung ist dabei umso genauer, je kleiner die Teilstücke gewählt werden. Daher wird zu infinitesimal kleinen Teilstücken (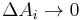$\Delta A_i\to 0$) übergangen, von denen es dann unendlich viele gibt (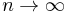$n\to\infty$). Auf diese Weise erhält man das entsprechende Flächenintegral:

$\Phi = \int\limits_A\vec{\textbf{B}}\cdot\mathrm{d}\vec{\textbf{A}} = \lim_{n\to\infty,\,\Delta A_i \to 0} = \sum_{i=1}^n \vec{\textbf{B}}_i\cdot\Delta\vec{\textbf{A}}_i$

Im Zusammenhang mit dem Flächenintegral treten häufig die folgenden Sonderfälle auf:

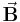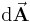Fall 1: Die Vektoren $\vec{\textbf{B}}$ und $\mathrm{d}\vec{\textbf{A}}$ sind überall parallel ($\vec{\textbf{B}} \parallel \mathrm{d}\vec{\textbf{A}}$):

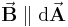In diesem Fall ist der eingeschlossene Winkel 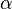$\alpha$ Null und der vektoriellen werden zu skalarwertigen Größen (vgl. Skalarprodukt):

$\Phi = \int_A B\,\mathrm{d}A$

Fall 2: Der Betrag 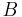$B$ der Flussdichte ist zusätzlich überall auf 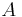$A$ konstant:

In diesem Fall geht die Integration in eine einfache Multiplikation über:

$\Phi = B \int_A\,\mathrm{d}A = B\,A$

Wie bereits geschildert, gibt es beim Flächenintegral zwei Integrationsvariablen und folglich auch zwei Integralzeichen (siehe Beispiel). Bei der gezeigten Variante wird nur ein Integralzeichen verwendet, da es sich um eine kompakte symbolische Schreibweise handelt und der Index 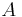$A$ des Integralzeichens bereits zur Kennzeichnung dieser Tatsache ausreicht. In der Literatur werden teilweise auch direkt zwei Integralzeichen angegeben:

$\Phi = \iint\limits_A\vec{\textbf{B}}\cdot\mathrm{d}\vec{\textbf{A}}$

Beispiel: Elektrisches Feld einer Punktladung Ein Beispiel zur Verwendung des Flächenintegrals findet sich im Artikel zur Lösung vektorieller Mehrfachintegrale.

Multimediale Lehrmaterialien

http://demonstrations.wolfram.com/DoubleIntegralForVolume/ Applet: Doppelintegral über ein Volumen mit Hilfe von Unter und Obersummen (engl./ free CDF-Player erforderlich)

Hilfreiche Links

http://www.uni-magdeburg.de/exph/mathe_gl/oberflaechenintegral.pdf Bebilderte Beschreibung zu Oberflächenintegralen http://math.intelarts.com/doubint1.htm Bebilderte Erläuterung zum Doppelintegral http://www-hm.ma.tum.de/integration/course/html/ch2/t/t_parent.htm Verschiedene Anwendungen der Integration http://www.uni-magdeburg.de/exph/mathe_gl/oberflaechenintegral2.pdf Detaillierte Beschreibung zum Oberflächenintegral mit Beispielrechnung http://mathworld.wolfram.com/SurfaceIntegral.html Formeln und kurze Erklärung zur Oberflächenintegration (engl.) http://www.ltcconline.net/greenl/courses/117/DoubIntProb/Volume.htm Erklärung zum Doppelintegral (engl.)

Literatur

• Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
• Wolfgang Pavel und Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
• Dr. Thomas Hempel, Mathematische Grundlagen, Linienintegral, Vorlesungsskript, Universität Magdeburg, 2010