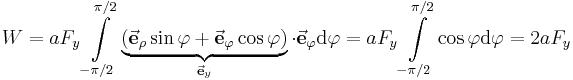Das Linienintegral
| ← Zurück: Erweiterung der Integralrechnung:Übersicht | Übersicht: Erweiterung der Integralrechnung | Vorwärts: Das Flächenintegral → |
Inhaltsverzeichnis
Das Linienintegral einer skalaren Größe
Das Linien- oder Kurvenintegral beschreibt eine Integration entlang einer (gerichteten) Kontur  , z. B. von einem Anfangspunkt
, z. B. von einem Anfangspunkt  bis zu einem Endpunkt
bis zu einem Endpunkt  . Dabei gibt es nur eine Integrationsvariable. Bei einer Integration entlang der
. Dabei gibt es nur eine Integrationsvariable. Bei einer Integration entlang der 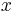 -Achse ist das zugehörige Differential beispielsweise durch
-Achse ist das zugehörige Differential beispielsweise durch  gegeben. Handelt es sich bei dem Integrationsweg
gegeben. Handelt es sich bei dem Integrationsweg 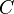 um eine geschlossene Kontur, d. h. der Anfangs- und Endpunkt fallen zusammen
um eine geschlossene Kontur, d. h. der Anfangs- und Endpunkt fallen zusammen  , wird das Linienintegral als Ring- oder Umlaufintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
, wird das Linienintegral als Ring- oder Umlaufintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
Das Linienintegral wird benötigt, wenn eine (ggf. vektorielle) Funktion von mehreren Variablen abhängt und entlang einer (im Allgemeinen nicht geradlinigen) Kontur zu integrieren ist. Dies ist zum Beispiel beim Durchflutungsgesetz (vgl. Erweiterung der Integralrechnung:Übersicht) der Fall. Prinzipiell handelt es sich um eine Erweiterung der Integralrechnung mit einer skalaren Funktion und nur einer Integrationsvariablen.
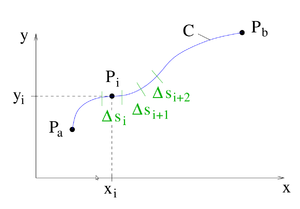
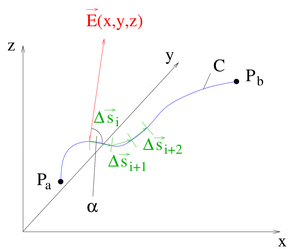
Zur Herleitung des Linienintegrals wird exemplarisch eine von zwei Variablen abhängige Funktion 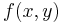 betrachtet, die entlang einer Kurve zwischen den Punkten
betrachtet, die entlang einer Kurve zwischen den Punkten 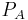 und
und 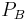 integriert werden soll (siehe Abbildung). Hierzu wird die Kontur zunächst in
integriert werden soll (siehe Abbildung). Hierzu wird die Kontur zunächst in 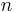 Teilstücke zerlegt. Dabei wird die Länge des
Teilstücke zerlegt. Dabei wird die Länge des 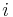 -ten Teilstücks mit
-ten Teilstücks mit 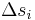 bezeichnet. Auf einem solchen
bezeichnet. Auf einem solchen 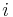 -ten Teilstück kann der jeweilige Funktionswert
-ten Teilstück kann der jeweilige Funktionswert 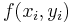 als näherungsweise konstant angenommen werden. Dadurch lässt sich ein Näherungswert für das Linienintegral dadurch angeben, dass die Produkte der Funktionswerte und den Längen der Teilstücke aufsummiert werden:
als näherungsweise konstant angenommen werden. Dadurch lässt sich ein Näherungswert für das Linienintegral dadurch angeben, dass die Produkte der Funktionswerte und den Längen der Teilstücke aufsummiert werden:
Es wurde bereits beschrieben, dass die Funktionswerte 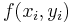 auf den Teilstücken als näherungsweise konstant angenommen werden können. Die Näherung ist dabei umso genauer, je kleiner die Teilstücke gewählt werden. Daher wird zu infinitesimal kleinen Teilstücken (
auf den Teilstücken als näherungsweise konstant angenommen werden können. Die Näherung ist dabei umso genauer, je kleiner die Teilstücke gewählt werden. Daher wird zu infinitesimal kleinen Teilstücken (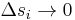 ) übergangen, von denen es dann unendlich viele gibt (
) übergangen, von denen es dann unendlich viele gibt (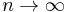 ). Auf diese Weise erhält man das entsprechende Linienintegral:
). Auf diese Weise erhält man das entsprechende Linienintegral:
Für eine möglichst einfache Lösung der Integrale bietet sich die Verwendung eines auf den jeweiligen Anwendungsfall „zugeschnittenen“ Koordinatensystems an.
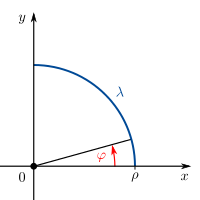
In diesem Beispiel werden verschiedene Fälle einer gegebenen Linienladung betrachtet. Bei einer Linienladung handelt es sich um eine Ladungsanordnung entlang einer Kontur. Dabei gibt die Linienladungsdichte Fall 1: Konstante und geradlinig angeordnete Linienladung Bei einer konstanten und entlang der Aufgrund der konstanten Linienladungsdichte kann die Gesamtladung folglich auch sofort ohne die Integration angegeben werden. Fall 2: Ortsabhängige und geradlinig angeordnete Linienladung Handelt es sich bei der Linienladungsdichte um eine ortsabhängige Größe, so kann das Ergebnis nicht einfach durch die Multiplikation dieser Größe mit der Strecke angegeben werden. Betrachtet wird zum Beispiel eine linear zunehmende Linienladungsdichte: Dabei ist Fall 3: Konstante und krummlinig angeordnete Linienladung In diesem Fall wird eine Linienladung in Form eines Viertelkreisbogens betrachtet. Da die Linienladungsdichte wieder konstant ist, muss diese zur Bestimmung der Gesamtladung lediglich mit der Länge dieses Viertelkreisbogens multipliziert werden. Dazu ist ein Übergang zu den Zylinderkoordinaten zweckmäßig. Mit Das verwendete Integral dient der Anschauung, alternativ kann die Länge des Viertelkreisbogens auch direkt als ein Viertel des Kreisumfangs angegeben werden. |
Das Linienintegral einer vektoriellen Größe
Linienintegrale treten häufig auch in vektorieller Form auf. Dabei ist eine vektorielle Funktion, z. B. 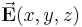 , entlang einer ebenfalls gerichteten Kontur mit den Wegelementen
, entlang einer ebenfalls gerichteten Kontur mit den Wegelementen 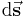 zu integrieren. Im Vergleich zum skalarwertigen Linienintegral ist also zusätzlich das Skalarprodukt
zu integrieren. Im Vergleich zum skalarwertigen Linienintegral ist also zusätzlich das Skalarprodukt  für jedes Wegelement
für jedes Wegelement 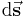 zu bestimmen. Aufgrund der Projektionseigenschaft das Skalarprodukts wird nur die jeweils tangential zum Wegelement verlaufende Kompotente des Vektors
zu bestimmen. Aufgrund der Projektionseigenschaft das Skalarprodukts wird nur die jeweils tangential zum Wegelement verlaufende Kompotente des Vektors 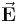 integriert. Für die weitere Herleitung wird ansonsten wie im skalarwertigen Fall verfahren.
integriert. Für die weitere Herleitung wird ansonsten wie im skalarwertigen Fall verfahren.
Die Kontur wird nun in 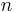 vektorielle Teilstücke zerlegt, wobei das
vektorielle Teilstücke zerlegt, wobei das 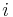 -te Teilelement mit
-te Teilelement mit 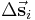 bezeichnet wird. Auf einem solchen
bezeichnet wird. Auf einem solchen 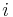 -ten Teilstück kann der jeweilige Funktionswert
-ten Teilstück kann der jeweilige Funktionswert 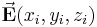 als näherungsweise konstant angenommen werden. Damit gilt für das Skalarprodukt bezogen auf das
als näherungsweise konstant angenommen werden. Damit gilt für das Skalarprodukt bezogen auf das 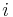 -te Teilstück:
-te Teilstück:
Damit folgt für das Linienintegral:
Für eine möglichst einfache Lösung der Integrale bietet sich auch hier die Verwendung eines auf den jeweiligen Anwendungsfall „zugeschnittenen“ Koordinatensystems an.
In der Lehrveranstaltung können derartige Integralberechnungen in der Regel auf zwei Spezialfälle reduziert werden.
Fall 1: Beide Vektoren verlaufen parallel (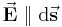 ): In diesem Fall liefert das Skalarprodukt der zugehörigen Vektoren den Wert Eins. Damit wird das Integral wieder skalarwertig.
): In diesem Fall liefert das Skalarprodukt der zugehörigen Vektoren den Wert Eins. Damit wird das Integral wieder skalarwertig.
Fall 2: Beide Vektoren stehen senkrecht aufeinander ( ): In diesem Fall liefert das Skalarprodukt der zugehörigen Vektoren den Wert Null und das Integral verschwindet.
): In diesem Fall liefert das Skalarprodukt der zugehörigen Vektoren den Wert Null und das Integral verschwindet.
Ein häufiger Anwendungsfall des Linienintegrals ergibt sich bei der Bestimmung der Spannung in einem elektrischen Feld. In diesem Beispiel wird die ortsunabhängige elektrische Feldstärke Um dieses Integral zu lösen, können vier Fälle unterschieden werden: Das Integral kann in diese vier Bereiche geteilt und das jeweilige Skalarprodukt ausgewertet werden: Daraus folgt: Aufgrund der eingeschlossenen rechten Winkel verbleibt: Da hier die Strecken zwischen Dies ist eine wichtige Erkenntnis im elektrostatischen Feld: Das Ringintegral ergibt hier immer Null. |
In diesem mechanischen Beispiel ist die Arbeit Die Laufrinne ist halbkreisförmig und beginnt am Anfangspunkt Der Bewegungsvorgang der Kugel lässt sich am einfachsten in Zylinderkoordinaten mit dem Koordinatenursprung im Mittelpunkt des Kreises beschrieben. Dabei bewegt sich die Kugel in Richtung wachsender Die vorgegebene Kraft lässt sich am einfachsten in kartesischen Koordinaten beschreiben: Mit Wandelt man nun noch den Einheitsvektor |
Multimediale Lehrmaterialien
|
http://www.dangries.com/Flash/IntegralSketch/IntegralSketch.html Applet zum Verständnis von Integralen |
Literatur
- Dr. Thomas Hempel, Mathematische Grundlagen, Linienintegral, Vorlesungsskript, Universität Magdeburg, 2010
- TU Freiberg, Parameter- und Kurvenintegrale, Script, 2010
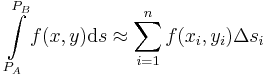

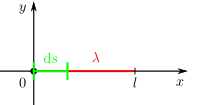
 die Ladungsmenge pro Streckenabschnitt an. Um die gesamte Ladung entlang einer Kontur berechnen zu können, muss die Linienladungsdichte entlang der jeweiligen Kontur integriert werden:
die Ladungsmenge pro Streckenabschnitt an. Um die gesamte Ladung entlang einer Kontur berechnen zu können, muss die Linienladungsdichte entlang der jeweiligen Kontur integriert werden:

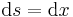 (vgl.
(vgl. 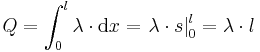

 eine Konstante mit der Einheit
eine Konstante mit der Einheit 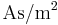 (ansonsten hätte
(ansonsten hätte 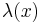 keine zu einer Linienladungsdichte passende Einheit
keine zu einer Linienladungsdichte passende Einheit 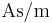 ). Die Linienladungsdichte wird also entlang der
). Die Linienladungsdichte wird also entlang der 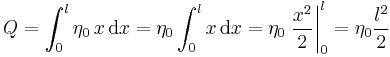
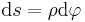 (vgl.
(vgl. 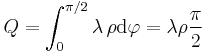
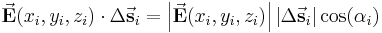
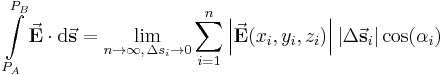

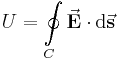
 bis
bis 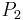 , die in die Richtung des elektrischen Feldes verläuft.
, die in die Richtung des elektrischen Feldes verläuft. bis
bis 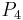 , die entgegen des elektrischen Feldes verläuft.
, die entgegen des elektrischen Feldes verläuft.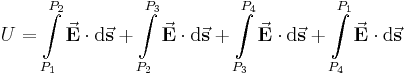

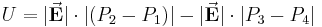
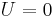
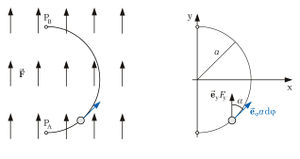
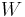 gesucht, die an einer Kugel verichtet wird, welche infolge einer Kraft
gesucht, die an einer Kugel verichtet wird, welche infolge einer Kraft 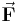 eine Laufrinne hinunterrollt:
eine Laufrinne hinunterrollt:
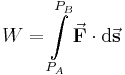
 -Werte auf einem Halbkreis mit konstantem Radius
-Werte auf einem Halbkreis mit konstantem Radius 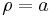 .
.
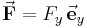
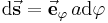 folgt also zunächst:
folgt also zunächst:
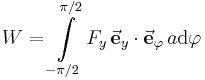
 in Zylinderkoordinaten um (vgl.
in Zylinderkoordinaten um (vgl.