Erweiterung der Integralrechnung:Übersicht
| ← Zurück: Volumenelemente | Übersicht: Erweiterung der Integralrechnung | Vorwärts: Das Linienintegral → |
Einführung
In der Lehrveranstaltung treten häufig Mehrfachintegrale auf, bei denen vektorielle Funktionen (meist Feldgrößen) z. B. über Konturen oder Flächen integriert werden. Beispiele hierfür sind der Satz von Gauß, das Induktionsgesetz oder das Durchflutungsgesetz.
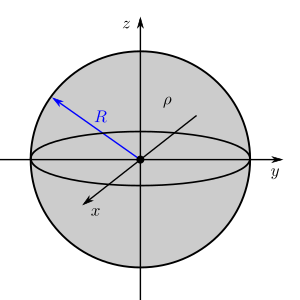
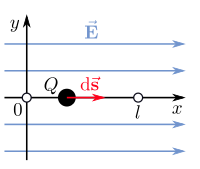
Einführend wird eine Punktladung 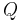 betrachtet, die in einem homogenen (d. h. ortsunabhängigen) elektrischen Feld
betrachtet, die in einem homogenen (d. h. ortsunabhängigen) elektrischen Feld 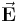 von einem Punkt
von einem Punkt  zu einem Punkt
zu einem Punkt 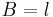 entlang der
entlang der  -Achse eines kartesischen Koordinatensystems bewegt wird (siehe Abbildung). Gesucht ist nun die Arbeit
-Achse eines kartesischen Koordinatensystems bewegt wird (siehe Abbildung). Gesucht ist nun die Arbeit 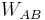 , die dabei verrichtet wird. Um
, die dabei verrichtet wird. Um 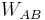 zu bestimmen, muss die dafür erforderliche Kraft
zu bestimmen, muss die dafür erforderliche Kraft 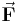 entlang des zurückgelegten Weges integriert werden:
entlang des zurückgelegten Weges integriert werden:
Durch das elektrische Feld 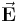 wirkt auf die Ladung
wirkt auf die Ladung 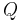 die Coulombkraft
die Coulombkraft 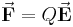 . Das elektrische Feld zeigt in die postive
. Das elektrische Feld zeigt in die postive  -Richtung, daher gilt
-Richtung, daher gilt 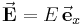 . Da die Ladung ausschließlich entlang der positiven
. Da die Ladung ausschließlich entlang der positiven  -Richtung verschoben wird, gilt
-Richtung verschoben wird, gilt 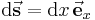 für das infinitesimale Wegelement. Diese Beziehungen können nun in das Wegintegral eingesetzt werden:
für das infinitesimale Wegelement. Diese Beziehungen können nun in das Wegintegral eingesetzt werden:
Dabei wurde ausgenutzt, dass die elektrische Feldstärke ortsunabhängig (also auch unabhängig von der Integrationsvariable  ) ist und somit vor das Integral geschrieben werden kann. Für das Skalarprodukt der Einheitsvektoren folgt weiterhin
) ist und somit vor das Integral geschrieben werden kann. Für das Skalarprodukt der Einheitsvektoren folgt weiterhin 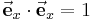 . Eine von der Ladung
. Eine von der Ladung  unabhängige Beziehung erhält man dadurch, dass man die Arbeit durch diese Größe dividiert:
unabhängige Beziehung erhält man dadurch, dass man die Arbeit durch diese Größe dividiert: 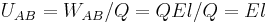 . Diese Größe bezeichnet man als Spannung.
. Diese Größe bezeichnet man als Spannung.
Ein weiteres Beispiel ist das Durchflutungsgesetz, dieses lautet wie folgt:
Das Durchflutungsgesetz sagt aus, dass die Integration der magnetischen Feldstärke 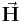 über eine geschlossene Kontur
über eine geschlossene Kontur 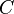 dem in der Fläche
dem in der Fläche 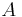 eingeschlossenen Strom
eingeschlossenen Strom 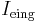 entspricht, die durch
entspricht, die durch 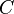 begrenzt wird. Magnetische Felder werden also von Strömen erzeugt und das Durchflutungsgesetz setzt beide Größen zueinander in Beziehung. Der Strom
begrenzt wird. Magnetische Felder werden also von Strömen erzeugt und das Durchflutungsgesetz setzt beide Größen zueinander in Beziehung. Der Strom 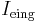 kann einfach durch die Integration der Stromdichte (entspricht der elektrischen Stromstärke bezogen auf die Fläche senkrecht zur Stromrichtung) über die Fläche
kann einfach durch die Integration der Stromdichte (entspricht der elektrischen Stromstärke bezogen auf die Fläche senkrecht zur Stromrichtung) über die Fläche 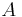 ermittelt werden. Die Fläche
ermittelt werden. Die Fläche 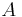 und die Kontur
und die Kontur 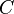 gehören folglich zusammen (eine Fläche wird immer von einer Kontur begrenzt). Analog verhält es sich bei Volumina, die stets durch eine geschlossene Hüllfläche begrenzt werden.
gehören folglich zusammen (eine Fläche wird immer von einer Kontur begrenzt). Analog verhält es sich bei Volumina, die stets durch eine geschlossene Hüllfläche begrenzt werden.
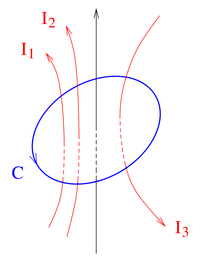
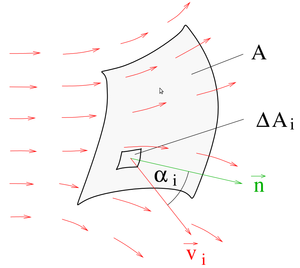
Für das Beispiel in der Abbildung kann der eingeschlossene Strom einfach durch Aufsummieren der einzelnen Ströme bestimmt werden:
In dem Integral handelt es sich um eine gerichtete Kontur 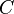 , da
, da 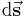 vektoriell ist. Entsprechend der gewählten Integrationsrichtung (im oder entgegen des Uhrzeigersinns) ist auch die Zählrichtung für die Ströme gemäß der Rechten-Hand-Regel I festgelegt.
vektoriell ist. Entsprechend der gewählten Integrationsrichtung (im oder entgegen des Uhrzeigersinns) ist auch die Zählrichtung für die Ströme gemäß der Rechten-Hand-Regel I festgelegt.
Für eine möglichst einfache Lösung der Integrale bietet sich die Verwendung eines auf den jeweiligen Anwendungsfall „zugeschnittenen“ Koordinatensystems an.
Die nachfolgende Übersicht zeigt die in der Lehrveranstaltungen vorkommenden Varianten von Integralen, die auf Artikel mit ausführlicheren Erklärungen verweisen. Wichtige Hinweise zur Lösung solcher Integrale finden sich im Artikel Lösung vektorieller Mehrfachintegrale.
Übersicht
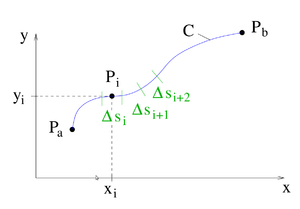
| Das Linienintegral
Das Linien- oder Kurvenintegral beschreibt eine Integration entlang einer (gerichteten) Kontur |
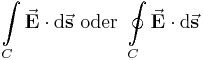 |
|
| Das Flächenintegral
Das Flächen- oder Oberflächenintegral beschreibt eine Integration über eine (gerichtete) Fläche. Da in diesem Fall eine Schachtelung von zwei Integrationsintervallen betrachtet wird, gibt es auch zwei Integrationsvariablen. Handelt es sich zum Beispiel um eine Fläche in der |
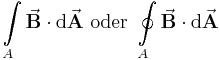 |
|
| Das Volumenintegral
Das Volumenintegral beschreibt eine Integration über ein Volumen. Damit handelt es sich um eine Schachtelung von drei Integrationsintervallen, so dass es auch genau drei Integrationsvariablen gibt. Das Differential |
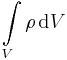 |
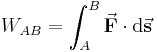
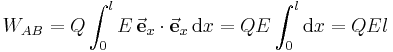
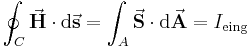
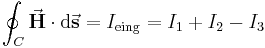
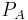 bis zu einem Endpunkt
bis zu einem Endpunkt 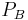 . Dabei gibt es nur eine Integrationsvariable. Bei einer Integration entlang der
. Dabei gibt es nur eine Integrationsvariable. Bei einer Integration entlang der 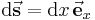 gegeben. Handelt es sich bei dem Integrationsweg
gegeben. Handelt es sich bei dem Integrationsweg  , wird das Linienintegral als Ring- oder Umlaufintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
, wird das Linienintegral als Ring- oder Umlaufintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
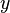 -Ebene eines
-Ebene eines 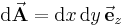 gegeben (Flächennormale zeigt hier in Richtung
gegeben (Flächennormale zeigt hier in Richtung 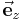 ). Handelt es sich um eine geschlossene Fläche (= Hüllfläche), so wird das Integral als Hüllflächenintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
). Handelt es sich um eine geschlossene Fläche (= Hüllfläche), so wird das Integral als Hüllflächenintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
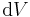 ist immer eine skalarwertige Größe, da einem Volumenelement keine Richtung zugeordnet werden kann. Soll zum Beispiel über ein Volumen innerhalb eines
ist immer eine skalarwertige Größe, da einem Volumenelement keine Richtung zugeordnet werden kann. Soll zum Beispiel über ein Volumen innerhalb eines 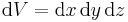 gegeben.
gegeben.