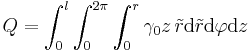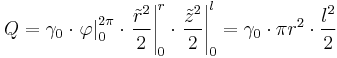Das Volumenintegral
| ← Zurück: Das Flächenintegral | Übersicht: Erweiterung der Integralrechnung | Vorwärts: Lineare Gleichungssysteme → |
Das Volumenintegral beschreibt eine Integration über ein Volumen. Damit handelt es sich um eine Schachtelung von drei Integrationsintervallen, so dass es auch genau drei Integrationsvariablen gibt. Das Differential 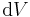 ist immer eine skalarwertige Größe, da einem Volumenelement keine Richtung zugeordnet werden kann. Soll zum Beispiel über ein Volumen innerhalb eines kartesischen Koordinatensystems integriert werden, so ist das zugehörige Differential durch
ist immer eine skalarwertige Größe, da einem Volumenelement keine Richtung zugeordnet werden kann. Soll zum Beispiel über ein Volumen innerhalb eines kartesischen Koordinatensystems integriert werden, so ist das zugehörige Differential durch 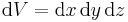 gegeben. Entsprechende Differentiale in anderen Koordinatensystemen sind in der Formelsammlung Koordinatensysteme angegeben.
gegeben. Entsprechende Differentiale in anderen Koordinatensystemen sind in der Formelsammlung Koordinatensysteme angegeben.
Ein häufiger Anwendungsfall des Volmenintegrals ist die Bestimmung der Gesamtladung bei vorgegebener Raumladungsdichte (siehe Beispiel unten).
Zur Herleitung des Volumenintegrals wird exemplarisch ein Würfel betrachtet, der über eine ortsabhängige Raumladungsdichte 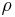 (=Ladungsmenge/Volumen) verfügt. Bei der Raumladungsdichte handelt es sich um eine analoge Größe zur Dichte eines Körpers, die die Masse pro Volumen beschreibt. Der Würfel kann nun in
(=Ladungsmenge/Volumen) verfügt. Bei der Raumladungsdichte handelt es sich um eine analoge Größe zur Dichte eines Körpers, die die Masse pro Volumen beschreibt. Der Würfel kann nun in 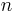 sehr kleine Teilstücke zerlegt werden, in denen die Raumladungsdichte jeweils näherungsweise konstant ist. Da die Raumladungsdichte die Ladungsmenge pro Volumen beschreibt, ergibt sich die Gesamtladung
sehr kleine Teilstücke zerlegt werden, in denen die Raumladungsdichte jeweils näherungsweise konstant ist. Da die Raumladungsdichte die Ladungsmenge pro Volumen beschreibt, ergibt sich die Gesamtladung 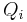 des
des 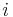 -ten Teilstücks des Würfels mit dem Volumen
-ten Teilstücks des Würfels mit dem Volumen 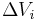 wie folgt:
wie folgt:
Die Gesamtladung des ganzen Würfels erhält man dann dadurch, dass man die Summe aus den Gesamtladungen der Teilstücke bildet:
Es wurde bereits beschrieben, dass die Raumladungsdichte in den Teilstücken als näherungsweise konstant angenommen werden kann. Die Näherung ist dabei umso genauer, je kleiner die Teilstücke gewählt werden. Daher wird zu infinitesimal kleinen Teilstücken (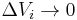 ) übergangen, von denen es dann unendlich viele gibt (
) übergangen, von denen es dann unendlich viele gibt (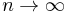 ). Auf diese Weise erhält man das entsprechende Volumenintegral:
). Auf diese Weise erhält man das entsprechende Volumenintegral:
In dem Beispiel wird über ein Volumen integriert, daher gibt es letztendlich drei Integrationsvariablen und folglich auch drei Integralzeichen (siehe Beispiel). Bei der gezeigten Variante wird nur ein Integralzeichen verwendet, da es sich um eine kompakte symbolische Schreibweise handelt und der Index 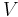 des Integralzeichens bereits zur Kennzeichnung dieser Tatsache ausreicht. In der Literatur werden teilweise auch direkt drei Integralzeichen angegeben:
des Integralzeichens bereits zur Kennzeichnung dieser Tatsache ausreicht. In der Literatur werden teilweise auch direkt drei Integralzeichen angegeben:
Fall 1: Konstante Raumladungsdichte In diesem Beispiel ist eine zylinderförmige Raumladung mit einer zunächst ortsunabhängigen (konstanten) Raumladungsdichte Aufgrund der Symmetrie der Anordnung ist die Verwendung von Zylinderkoordinaten zweckmäßig. Das Differential Da hier der (konstante) Radius des Zylinders bereits mit Für die Gesamtladung folgt damit: Da Dieses Ergebnis ist plausibel, da die Raumladungsdichte mit dem Volumen des Zylinders multipliziert wird. Aufgrund der konstanten Raumladungsdichte kann die Gesamtladung folglich auch sofort ohne die Integration angegeben werden. Fall 2: Ortsabhängige Raumladungsdichte Handelt es sich bei der Raumladungsdichte um eine ortsabhängige Größe, so kann das Ergebnis nicht einfach durch die Multiplikation dieser Größe mit dem Volumen angegeben werden. Betrachtet wird zum Beispiel eine linear zunehmende Raumladungsdichte: Dabei ist Setzt man diese ortsabhängige Raumladungsdichte in das Integral ein, so folgt: Die Konstante Weitere Hinweise finden sich im Artikel zur Lösung von Mehrfachintegralen. |
Ein weiteres Beispiel zur Verwendung des Volumenintegrals findet sich im Artikel Volumenelemente. |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/DoubleIntegralForVolume/ Applet: Doppelintegral über ein Volumen mit Hilfe von Unter und Obersummen (engl./ free CDF-Player erforderlich) |
Hilfreiche Links
|
http://www.tphys.physik.uni-tuebingen.de/muether/physik1/skript/03-02.pdf Bebilderte Beschreibung zum Volumenintegral am Beispiel von Massepunkten http://www-hm.ma.tum.de/integration/course/html/ch2/t/t_parent.htm Verschiedene Anwendungen der Integration http://www.tphys.physik.uni-tuebingen.de/muether/physik1/skript/03-02.pdf Bebilderte Beschreibung zum Volumenintegral am Beispiel von Massepunkten |
Literatur
- Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Klaus Jänich, Mathematik 1. Geschrieben für Physiker, 2. Auflage (Springer Berlin Heidelberg, 2005)
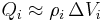
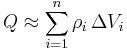
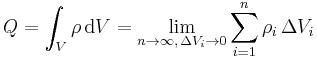
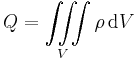
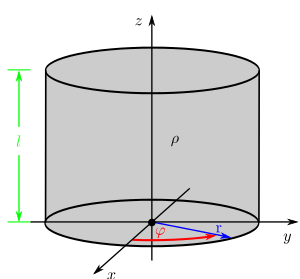
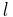 und den Radius
und den Radius 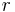 . Ziel ist es nun, die gesamte Ladungsmenge
. Ziel ist es nun, die gesamte Ladungsmenge 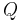 (Gesamtladung) des Zylinders zu bestimmen. Hierfür muss die Raumladungsdichte über das Volumen
(Gesamtladung) des Zylinders zu bestimmen. Hierfür muss die Raumladungsdichte über das Volumen 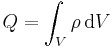
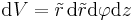
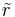 bezeichnet.
bezeichnet.
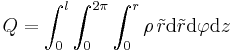
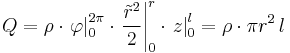

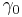 eine Konstante mit der Einheit
eine Konstante mit der Einheit 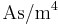 (ansonsten hätte
(ansonsten hätte 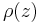 keine zu einer Raumladungsdichte passende Einheit
keine zu einer Raumladungsdichte passende Einheit 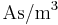 ). Die Raumladungsdichte wird also entlang der
). Die Raumladungsdichte wird also entlang der 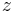 -Achse größer.
-Achse größer.