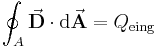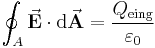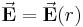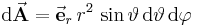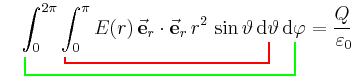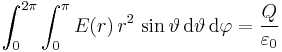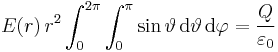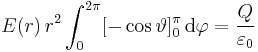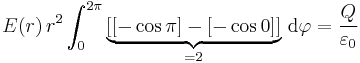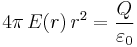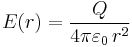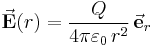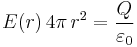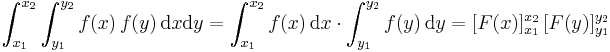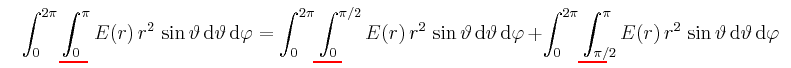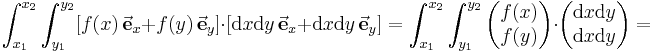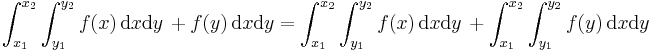Lösung vektorieller Mehrfachintegrale
In diesem Artikel wird die Vorgehensweise zur Lösung vektorieller Mehrfachintegrale anhand eines Beispiels (Satz von Gauß) beschrieben. Dabei wird auch auf Aspekte wie die Integrationsreihenfolge und die verwendete Schreibweise eingegangen.
Inhaltsverzeichnis
Elektrische Feldstärke einer Punktladung
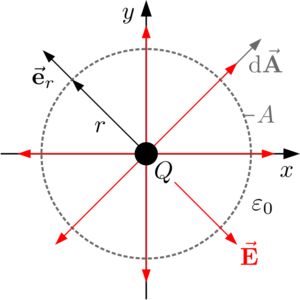
Betrachtet wird eine Punktladung  , die sich im Ursprung eines kartesischen Koordinatensystems befindet (siehe Abbildung, diese zeigt einen Querschnitt der Anordnung). Ziel ist es nun, im gesamten Raum die von dieser Punktladung hervorgerufene elektrische Feldstärke
, die sich im Ursprung eines kartesischen Koordinatensystems befindet (siehe Abbildung, diese zeigt einen Querschnitt der Anordnung). Ziel ist es nun, im gesamten Raum die von dieser Punktladung hervorgerufene elektrische Feldstärke 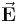 zu bestimmen.
zu bestimmen.
Ausgangspunkt hierfür ist zunächst der Satz von Gauß:
Der Satz besagt, dass die Integration der elektrischen Flussdichte 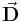 (dabei handelt es sich hier um eine zur elektrischen Feldstärke proportionale Größe) über eine beliebige geschlossene Hüllfläche
(dabei handelt es sich hier um eine zur elektrischen Feldstärke proportionale Größe) über eine beliebige geschlossene Hüllfläche  der darin eingeschlossenen Ladung
der darin eingeschlossenen Ladung 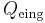 entspricht. Da eine Hüllfläche stets ein Volumen umschließt, kann auch von der im umschlossenen Volumen befindlichen Ladung
entspricht. Da eine Hüllfläche stets ein Volumen umschließt, kann auch von der im umschlossenen Volumen befindlichen Ladung 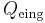 gesprochen werden. Die geschlossene Hüllfläche ist deshalb beliebig wählbar, weil der Satz keine Aussage über deren Form trifft.
gesprochen werden. Die geschlossene Hüllfläche ist deshalb beliebig wählbar, weil der Satz keine Aussage über deren Form trifft.
Der Index 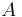 des Integralzeichens gehört zum vektoriellen Differential
des Integralzeichens gehört zum vektoriellen Differential 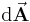 und gibt an, dass es sich um eine gerichtete (gerichtet weil vektoriell) Fläche (englisch area) handelt. Da das Integralzeichen weiterhin mit einem Ring dargestellt wird, handelt es sich hierbei um eine geschlossene Fläche (= Hüllfläche). Daher spricht man hier auch von einem Hüllflächenintegral. Der Punkt symbolisiert, dass zwischen den beiden Vektoren
und gibt an, dass es sich um eine gerichtete (gerichtet weil vektoriell) Fläche (englisch area) handelt. Da das Integralzeichen weiterhin mit einem Ring dargestellt wird, handelt es sich hierbei um eine geschlossene Fläche (= Hüllfläche). Daher spricht man hier auch von einem Hüllflächenintegral. Der Punkt symbolisiert, dass zwischen den beiden Vektoren 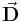 und
und 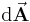 das Skalarprodukt auszuführen ist.
das Skalarprodukt auszuführen ist.
Die elektrische Flussdichte 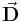 ist (hier) mit der elektrischen Feldstärke
ist (hier) mit der elektrischen Feldstärke 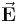 gemäß
gemäß 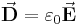 verknüpft. Diese Gleichung kann nach
verknüpft. Diese Gleichung kann nach 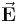 umgestellt und in den Satz von Gauß eingesetzt werden, so dass folgt:
umgestellt und in den Satz von Gauß eingesetzt werden, so dass folgt:
Bei einer Punktladung handelt es sich zwar um ein Modell für eine Ladung ohne räumliche Ausdehnung, prinzipiell kann jedoch auch von der Form einer unendlich kleinen Kugel ausgegangen werden. Zur Bestimmung der elektrischen Feldstärke bietet sich damit die Verwendung von Kugelkoordinaten an. Aufgrund der Symmetrie der Kugel folgt, dass auch das elektrische Feld kugelsymmetrisch sein muss und folglich ausschließlich vom Abstand  vom Koordinatenursprung abhängt:
vom Koordinatenursprung abhängt:
Aus der Kugelsymmetrie folgt weiterhin, dass die elektrische Feldstärke radialsymmetrisch gerichtet ist, also stets in Richtung des Einheitsvektors 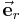 zeigt (vgl. Abbildung oben). Damit kann der Vektor der elektrischen Feldstärke als Produkt seines Betrags und des genannten Richtungsvektors ausgedrückt werden (vgl. Komponentendarstellung von Vektoren):
zeigt (vgl. Abbildung oben). Damit kann der Vektor der elektrischen Feldstärke als Produkt seines Betrags und des genannten Richtungsvektors ausgedrückt werden (vgl. Komponentendarstellung von Vektoren):
Um den Satz von Gauß anwenden zu können, ist die Wahl einer (beliebigen) geschlossenen Hüllfläche erforderlich. Hier ist nun die Verwendung einer kugelförmigen Hüllfäche zweckmäßig, von der 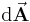 ein infinitesimales Flächenelement darstellt, welches auf der Oberfläche der Hüllfläche ebenfalls immer in Richtung
ein infinitesimales Flächenelement darstellt, welches auf der Oberfläche der Hüllfläche ebenfalls immer in Richtung 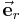 zeigt (vgl. Abbildung oben):
zeigt (vgl. Abbildung oben):
Da die Punktladung als unendlich kleine Kugel aufgefasst wird, ist die in der Hüllfläche (deren Größe durch den gerade betrachteten Radius  gegeben ist) eingeschlossene Ladung immer durch
gegeben ist) eingeschlossene Ladung immer durch 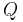 gegeben (ohne Koordinatenursprung), so dass die rechte Seite des Integrals konstant bleibt. Setzt man die ermittelten Zusammenhänge ein, so folgt:
gegeben (ohne Koordinatenursprung), so dass die rechte Seite des Integrals konstant bleibt. Setzt man die ermittelten Zusammenhänge ein, so folgt:
Die Integrationsgrenzen in Kugelkoordinaten werden so gewählt, dass diese die gesamte Kugeloberfläche (sonst wäre es keine geschlossene Hüllfläche) erfassen. Die Winkel müssen dabei unbedingt im Bogenmaß angegeben werden.
Bei der Zuordnung der Integrationsvariablen zu den jeweiligen Integralzeichen mit den Grenzen gilt die Konvention "von innen nach außen" (siehe Markierungen). Die Reihenfolge der Integration spielt jedoch keine Rolle und wird hintereinander ausgeführt, d. h. es kann wahlweise zuerst nach 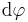 oder
oder 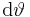 integriert werden. Die zu den jeweiligen Variablen gehörenden Integrationsgrenzen bleiben aber erhalten. Je nach Integral kann eine geschickte Wahl der Integrationsreihenfolge auch zu Vereinfachungen führen.
integriert werden. Die zu den jeweiligen Variablen gehörenden Integrationsgrenzen bleiben aber erhalten. Je nach Integral kann eine geschickte Wahl der Integrationsreihenfolge auch zu Vereinfachungen führen.
In der obigen Gleichung wird zunächst das Skalarprodukt der Einheitsvektoren bestimmt (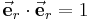 ) und man erhält:
) und man erhält:
Der Term 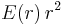 hängt nicht von den Integrationsvariablen
hängt nicht von den Integrationsvariablen 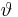 und
und  ab, so dass dieser vor das Integral geschrieben werden kann:
ab, so dass dieser vor das Integral geschrieben werden kann:
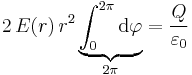
Nun kann zunächst die Integration nach 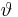 ausgeführt werden (wahlweise auch nach
ausgeführt werden (wahlweise auch nach  ):
):
Damit folgt:
Das Ergebnis der ersten Integration ist also unabhängig von der verbleibenden Integrationsvariable  und kann daher ebenfalls vor das Integral geschrieben werden:
und kann daher ebenfalls vor das Integral geschrieben werden:
Das verbleibende Integral liefert 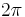 , so dass sich insgesamt die folgende Gleichung ergibt:
, so dass sich insgesamt die folgende Gleichung ergibt:
Der Betrag der elektrischen Feldstärke ergibt sich damit durch einfaches Umstellen:
Durch das Skalarprodukt im Satz von Gauß geht also die Richtungsinformation verloren, allerdings wurde ja bereits der Zusammenhang 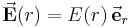 beschrieben. Insgesamt gilt damit (ausgenommen ist der Punkt
beschrieben. Insgesamt gilt damit (ausgenommen ist der Punkt 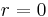 , da der Term dort wegen der Division durch 0 nicht definiert ist):
, da der Term dort wegen der Division durch 0 nicht definiert ist):
Hinweise
Vermeidung der Integration
Ist die zu integrierende Funktion unabhängig von sämtlichen Integrationsvariablen, so kann diese direkt vor das Integral geschrieben und das Ergebnis des Integrals sofort angegeben werden. In dem obigen Beispiel gilt:
Für das Differential gilt außerdem:
Nach der Ausführung des Skalarprodukts der Einheitsvektoren kann der Term 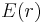 vor das Integral geschrieben werden:
vor das Integral geschrieben werden:
Für das Integral kann folglich direkt die Oberfläche einer Kugel angegeben werden ( ), so dass die Integration hier gar nicht explizit ausgeführt werden muss:
), so dass die Integration hier gar nicht explizit ausgeführt werden muss:
Ähnliche Fälle können sich zum Beispiel bei der Integration über Konturen (z. B. Kreise) oder Volumina ergeben.
Vereinfachungen bei der Integration
Sind die zu integrierenden Funktionen unabhängig voneinander, so können die jeweiligen Ergebnisse der einzelnen Integrale einfach multipliziert werden:
Dabei bezeichnen 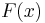 und
und 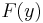 die zu
die zu 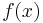 bzw.
bzw.  gehörenden Stammfunktionen. Für das oben auftretende Integral gilt damit:
gehörenden Stammfunktionen. Für das oben auftretende Integral gilt damit:
Zerlegung von Hüllflächen
Je nach gewählter Hüllfläche kann es sinnvoll sein, diese in Teilflächen zu zerlegen und die Integration als Summe über diese Teilflächen anzugeben. Liegt beispielsweise eine zylinderförmige Hüllfläche vor, so kann separat über Boden, Deckel und Mantel integriert werden. Dabei müssen alle Teilflächen zusammen die geschlossene Hüllfläche ergeben.
Obwohl dies in dem obigen Beispiel nicht erforderlich ist, kann auch die kugelförmige Hüllfläche in eine obere und untere Halbkugel zerlegt werden:
Ähnliche Fälle können sich zum Beispiel bei der Integration über Konturen (z. B. Kreise) oder Volumina ergeben.
Symbolische Schreibweise des Integrals
In dem Beispiel wird über eine Fläche integriert, daher gibt es letztendlich zwei Integrationsvariablen und folglich auch zwei Integralzeichen. Im Satz von Gauß wird nur ein Integralzeichen verwendet, da es sich um eine kompakte symbolische Schreibweise handelt und der Index 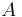 des Integralzeichens bereits zur Kennzeichnung dieser Tatsache ausreicht. In der Literatur werden teilweise auch direkt zwei Integralzeichen angegeben. Analog wird bei Volumenintegralen vorgegangen.
des Integralzeichens bereits zur Kennzeichnung dieser Tatsache ausreicht. In der Literatur werden teilweise auch direkt zwei Integralzeichen angegeben. Analog wird bei Volumenintegralen vorgegangen.
Ausführung des Skalarprodukts
Es kann vorkommen, dass die Vektoren 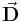 und
und 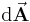 im Integral über mehrere Komponenten verfügen. In diesem Fall liefert das Skalarprodukt eine Summe von Termen, über die einfach separat integriert werden kann. Ein einfaches Beispiel in kartestischen Koordinaten verdeutlicht dies:
im Integral über mehrere Komponenten verfügen. In diesem Fall liefert das Skalarprodukt eine Summe von Termen, über die einfach separat integriert werden kann. Ein einfaches Beispiel in kartestischen Koordinaten verdeutlicht dies: