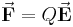Einführung in die Vektorrechnung
| ← Zurück: Übersicht Vektorrechnung | Übersicht: Vektorrechnung | Vorwärts: Einheitsvektoren → |
|
Zu diesem Thema stehen Aufgaben zur Selbstkontrolle zur Verfügung. |
Eine ganze Reihe physikalischer Größen lässt sich bereits durch die Angabe eines Zahlenwertes und der dazugehörigen Einheit vollständig beschreiben. Solche Größen nennt man skalare Größen oder kurz Skalare, gängige Beispiele sind die Masse eines Körpers (zum Beispiel 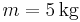 ) oder die Temperatur in einem Punkt im Raum (zum Beispiel
) oder die Temperatur in einem Punkt im Raum (zum Beispiel 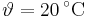 oder
oder 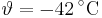 ). Andere physikalische Größen sind gerichtet, so dass zur vollständigen Beschreibung zusätzlich die Angabe einer Richtung erforderlich ist. In diesem Fall spricht man von vektoriellen Größen. Bekannte Beispiele hierfür sind die Geschwindigkeit und alle Arten von Kräften.
). Andere physikalische Größen sind gerichtet, so dass zur vollständigen Beschreibung zusätzlich die Angabe einer Richtung erforderlich ist. In diesem Fall spricht man von vektoriellen Größen. Bekannte Beispiele hierfür sind die Geschwindigkeit und alle Arten von Kräften.
Zur Unterscheidung von skalaren und vektoriellen Größen werden letztere häufig mit einem Pfeil (zum Beispiel  ) gekennzeichnet. Physikalische Zusammenhänge mit vektoriellen Größen lassen sich dann durch Größengleichungen beschreiben, deren mathematische Behandlung nach den Regeln der Vektorrechnung erfolgt. Weiterhin erfüllen die Größengleichungen die Gleichheitsbeziehung jeweils für die Zahlenwerte, Einheiten und Richtungen.
) gekennzeichnet. Physikalische Zusammenhänge mit vektoriellen Größen lassen sich dann durch Größengleichungen beschreiben, deren mathematische Behandlung nach den Regeln der Vektorrechnung erfolgt. Weiterhin erfüllen die Größengleichungen die Gleichheitsbeziehung jeweils für die Zahlenwerte, Einheiten und Richtungen.
Zur graphischen Darstellung von Vektoren werden Pfeile verwendet, deren Richtung die Orientierung eines Vektors angibt und deren Länge dem jeweiligen Betrag entspricht. Der Betrag 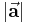 eines Vektors
eines Vektors 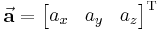 (das
(das 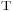 steht für Transposition und ermöglicht die Schreibweise des Spaltenvektors als Zeilenvektor) lässt sich wie folgt bestimmen:
steht für Transposition und ermöglicht die Schreibweise des Spaltenvektors als Zeilenvektor) lässt sich wie folgt bestimmen:
Da die vorgestellte Schreibweise für den Betrag vergleichsweise aufwändig ist, schreibt man häufig einfach 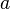 statt
statt 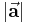 . Der Vektor
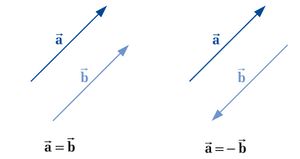
. Der Vektor 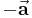 hat den gleichen Betrag wie der Vektor
hat den gleichen Betrag wie der Vektor  , jedoch zeigt dieser in die entgegengesetzte Richtung. Zwei oder mehr Vektoren nennt man gleich, wenn deren Beträge und Richtungen übereinstimmen. Ein spezieller Vektor ist der Nullvektor
, jedoch zeigt dieser in die entgegengesetzte Richtung. Zwei oder mehr Vektoren nennt man gleich, wenn deren Beträge und Richtungen übereinstimmen. Ein spezieller Vektor ist der Nullvektor 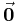 mit unbestimmter Richtung und dem Betrag 0.
mit unbestimmter Richtung und dem Betrag 0.
Betrachtet man die Bewegung eines Flugkörpers, so hat dieser zu jedem Zeitpunkt |
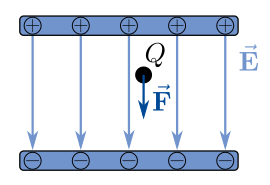
Befindet sich eine punktförmige Ladung mit der Ladungsmenge Die zugehörige vektorielle Größengleichung lautet wie folgt: Die Ladungsmenge |
Charakterisierung von Vektoren
Abhängig von den jeweiligen Eigenschaften lassen sich Vektoren u. a. wie folgt charakterisieren:
- Freier Vektor: Freie Vektoren können beliebig im Raum verschoben werden und sind nicht an einen festen Anfangspunkt gebunden. In diesem Fall lassen sich gleiche Vektoren durch Parallelverschiebung zur Deckung bringen.
- Gebundener Vektor: Gebundene Vektoren können nicht verschoben werden und besitzen einen festen Angriffspunkt. Betrachtet man beispielsweise eine ortsabhängige elektrische Feldstärke, so sind Richtung und Betrag der entsprechenden Vektoren bestimmten Punkten im Raum zugeordnet.
- Ortsvektor: Ortsvektoren beginnen in der Regel im Ursprung eines gegebenen Koordinatensystems und sind in diesem Sinne gebundene Vektoren. Hinzu kommt, dass Ortsvektoren ausgehend vom Ursprung auf bestimmte Punkte (Orte), z. B. auf die Position einer Punktladung, im dreidimensionalen Raum zeigen.
Multimediale Lehrmaterialien
|
http://www.walter-fendt.de/html5/mde/line3d_de.htm Applet: Vektorgleichung einer Geraden im dreidimensionalen Raum |
Hilfreiche Links
|
http://www.mathe-online.at/mathint/vect1/i.html Allgemeine Einführung in die Vektorrechnung http://www.tf.uni-kiel.de/matwis/amat/mw1_ge/kap_3/basics/m3_1_1.html Übersicht zur Vektorrechnung |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
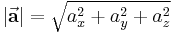
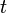 nicht nur eine aktuelle Geschwindigkeit
nicht nur eine aktuelle Geschwindigkeit 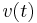 , sondern zusätzlich eine Bewegungsrichtung. Folglich handelt es sich bei der Geschwindigkeit um eine vektorielle Größe, das heißt es gilt
, sondern zusätzlich eine Bewegungsrichtung. Folglich handelt es sich bei der Geschwindigkeit um eine vektorielle Größe, das heißt es gilt 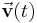 . Die zugehörige gerichtete Strecke ergibt sich dann aus dem Produkt dieser Größe und der Zeit:
. Die zugehörige gerichtete Strecke ergibt sich dann aus dem Produkt dieser Größe und der Zeit:
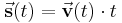
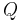 in einem elektrischen Feld
in einem elektrischen Feld 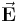 , so wirkt eine Kraft
, so wirkt eine Kraft 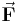 auf diese Ladung. Ein elektrisches Feld bildet sich zum Beispiel zwischen zwei positiv und negativ geladenen Platten aus (siehe nachfolgende Abbildung eines Kondensators).
auf diese Ladung. Ein elektrisches Feld bildet sich zum Beispiel zwischen zwei positiv und negativ geladenen Platten aus (siehe nachfolgende Abbildung eines Kondensators).