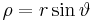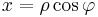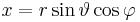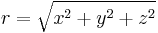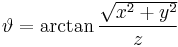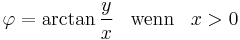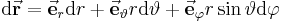Kugelkoordinaten
| ← Zurück: Zylinderkoordinaten | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Differentialquotient → |
Das Kugelkoordinatensystem ermöglicht insbesondere dann eine kompakte Beschreibung von Positionen und gerichteten Größen im Raum, wenn man es mit kugelförmigen Anordnungen zu tun hat. Das elektrische Feld einer Punktladung, die näherungsweise als kugelförmig angenommen werden kann, lässt sich zum Beispiel wesentlich einfacher in Kugel- als in kartesischen Koordinaten beschreiben (vgl. Einführung in der Übersicht zu orthogonalen Koordinatensystemen sowie Lösung vektorieller Mehrfachintegrale). Es gibt einige weitere Beispiele wie etwa die Beschreibung des elektrischen Feldes einer kugelförmigen Raumladung. Bei dem Kugelkoordinatensystem handelt es sich um ein krummliniges orthogonales Koordinatensystem.
Bei dem Kugelkoordinatensystem wird ein Punkt 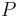 im Raum durch die drei Koordinaten
im Raum durch die drei Koordinaten 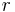 ,
, 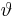 und
und  beschrieben. Dabei bezeichnet
beschrieben. Dabei bezeichnet 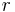 den Abstand des betrachteten Punktes vom Koordinatenursprung.
den Abstand des betrachteten Punktes vom Koordinatenursprung. 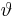 gibt den Winkel zwischen der positiven
gibt den Winkel zwischen der positiven 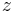 -Achse und dem vom Ursprung zum betrachteten Punkt zeigenden Ortsvektor an. Der Winkel durchläuft dabei den Wertebereich
-Achse und dem vom Ursprung zum betrachteten Punkt zeigenden Ortsvektor an. Der Winkel durchläuft dabei den Wertebereich 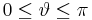 , so dass der positiven
, so dass der positiven 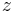 -Achse der Wert
-Achse der Wert 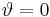 und der negativen
und der negativen 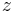 -Achse der Wert
-Achse der Wert 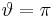 zugeordnet ist (Achtung: Fälschlicherweise wird häufig ein Wertebereich von
zugeordnet ist (Achtung: Fälschlicherweise wird häufig ein Wertebereich von 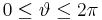 angenommen). Der Winkel
angenommen). Der Winkel  wird wie bei den Zylinderkoordinaten gezählt, also ausgehend von der positiven
wird wie bei den Zylinderkoordinaten gezählt, also ausgehend von der positiven  -Achse in Richtung der positiven
-Achse in Richtung der positiven 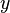 -Achse. Betrachtet man die Koordinatenfläche
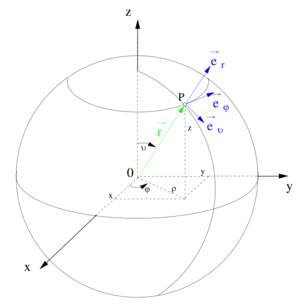
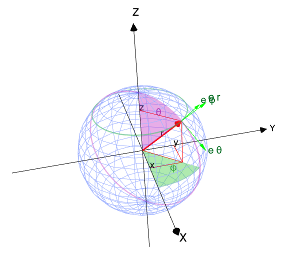
-Achse. Betrachtet man die Koordinatenfläche 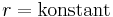 , so entspricht diese einer konzentrisch um den Ursprung liegenden Kugelfläche (vgl. Abbildung). Alle Punkte mit identischem
, so entspricht diese einer konzentrisch um den Ursprung liegenden Kugelfläche (vgl. Abbildung). Alle Punkte mit identischem 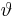 liegen dabei auf einem „Breitengrad” und Punkte mit identischem
liegen dabei auf einem „Breitengrad” und Punkte mit identischem  liegen auf einem „Längengrad“.
liegen auf einem „Längengrad“.
Die Richtung der Einheitsvektoren 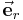 ,
, 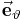 und
und 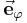 hängt stets von der Position des betrachteten Punktes ab. Die nebenstehende Abbildung verdeutlicht, dass
hängt stets von der Position des betrachteten Punktes ab. Die nebenstehende Abbildung verdeutlicht, dass 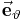 und
und 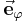 immer tangential zu den Kreisbögen der
immer tangential zu den Kreisbögen der 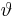 -Koordinatenlinie bzw.
-Koordinatenlinie bzw.  -Koordinatenlinie im Punkt
-Koordinatenlinie im Punkt 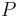 verlaufen und
verlaufen und 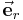 immer in Richtung des Ortsvektors
immer in Richtung des Ortsvektors 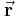 zeigt.
zeigt.
Die Koordinaten und Einheitsvektoren der verschiedenen Koordinatensysteme können mit Hilfe von Transformationsgleichungen ineinander umgerechnet werden (siehe hierzu Formelsammlung Koordinatensysteme). Möchte man beispielsweise den Wert  in kartesischen Koordinaten eines in Kugelkoordinaten gegebenen Punktes
in kartesischen Koordinaten eines in Kugelkoordinaten gegebenen Punktes 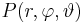 ermitteln, so bietet sich die Verwendung trigonometrischer Funktionen an. Aus der Abbildung wird ersichtlich, dass hierzu zunächst die Strecke
ermitteln, so bietet sich die Verwendung trigonometrischer Funktionen an. Aus der Abbildung wird ersichtlich, dass hierzu zunächst die Strecke 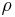 in der
in der  -
-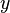 -Ebene zu bestimmen ist:
-Ebene zu bestimmen ist:
Weiterhin ist ersichtlich, dass 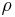 der Hypotenuse und
der Hypotenuse und  der Ankathete in Bezug auf das durch
der Ankathete in Bezug auf das durch  gegebene rechtwinklige Dreieck entspricht. Damit gilt:
gegebene rechtwinklige Dreieck entspricht. Damit gilt:
Setzt man nun 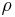 in die untere Gleichung ein, so erhält man:
in die untere Gleichung ein, so erhält man:
Weitere Umrechnungen lassen sich analog herleiten und sind in der folgenden Tabelle angegeben:
| Umrechnung von Kugel- in kartesische Koordinaten |
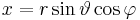
|
Umrechnung von kartesischen- in Kugelkoordinaten |
|
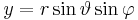
|
| ||
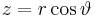
|
|
Eine differentielle (infinitesimale) Änderung des Ortsvektors 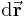 ausgehend vom Punkt
ausgehend vom Punkt 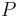 um
um 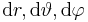 wird wie folgt beschrieben:
wird wie folgt beschrieben:
Für weitere Umrechnungen und Zusammenhänge wird auf die Formelsammlung Koordinatensysteme verwiesen.
Je nachdem, in welchen Bereichen (Intervallen) sich die Koordinaten bewegen, werden verschiedene Linien-, Flächen- und Volumenelemente beschrieben. Hält man z. B. alle Koordinaten bis auf  konstant, so ergeben sich „Breitengrade“ (vgl. Koordinatenlinien). Zur Verdeutlichung dieser Zusammenhänge kann das unten eingebundene Applet verwendet werden.
konstant, so ergeben sich „Breitengrade“ (vgl. Koordinatenlinien). Zur Verdeutlichung dieser Zusammenhänge kann das unten eingebundene Applet verwendet werden.
Applet
Ein Beispiel zur Verwendung von Kugelkoordinaten zur Beschreibung des elektrischen Feldes einer Punktladung findet sich im Artikel zur Lösung vektorieller Mehrfachintegrale. |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/ExploringSphericalCoordinates/ Applet: Punkt in Polarkoordinaten (engl./ free CDF-Player von Wolfram erforderlich) http://demonstrations.wolfram.com/SphericalCoordinates/ Applet: Punkt in Polarkoordinaten (engl. / free CDF-Player erforderlich) |
Hilfreiche Links
|
http://de.academic.ru/pictures/dewiki/83/Sphere_3d.png dreidimensionales Bild zur Bestimmung eines Punktes in Kugelkoordinaten http://mathworld.wolfram.com/PolarCoordinates.html Allgemeine Einführung in die Polarkoordinaten (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)