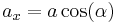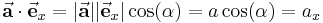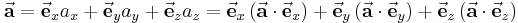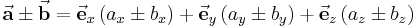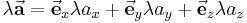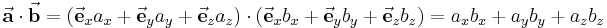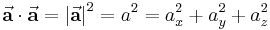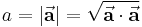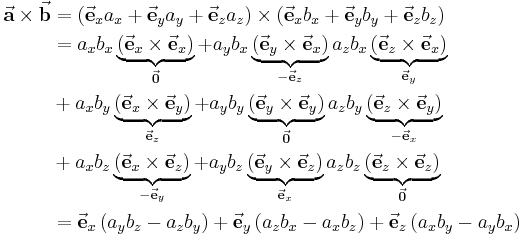Komponentendarstellung von Vektoren

← Zurück: Vektorprodukt

Übersicht: Vektorrechnung

Vorwärts: Formelsammlung zur Vektorrechnung →

Zu diesem Thema stehen Aufgaben zur Selbstkontrolle zur Verfügung.

Komponentenzerlegung eines Vektors

Vektorzerlegung

Bestimmung der Komponenten

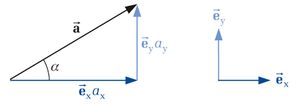
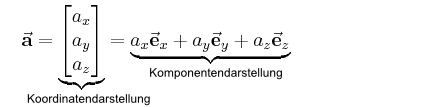
Betrachtet man beispielsweise einen Vektor $\vec{\textbf{a}}$ im dreidimensionalen kartesischen Koordinatensystem, so lässt sich dieser auch als Summe der Produkte seiner Komponenten und den zugehörigen Einheitsvektoren, die in die Richtungen der jeweiligen Koordinatenachsen zeigen, angeben:

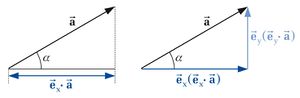
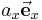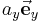Die Schreibweise mit den Klammern heißt Koordinatendarstellung, die andere Komponentendarstellung. Die Gültigkeit dieses Zusammenhangs lässt sich anhand des zweidimensionalen Beispiels in der Abbildung zur Vektorzerlegung nachvollziehen: Bildet man die Summe der beiden Vektoren $a_x \vec{\textbf{e}}_x$ und $a_y \vec{\textbf{e}}_y$, so erhält man wieder den ursprünglichen Vektor $\vec{\textbf{a}}$. 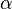Führt man nun wie dargestellt einen Winkel $\alpha$ ein, so lässt sich feststellen, dass sich die Strecke 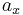$a_x$ mit Hilfe des Kosinus wie folgt bestimmen lässt:

$a_x = a \cos(\alpha)$

Mit Hilfe des Skalarprodukts (geometrisch interpretiert auch weil sich die Strecke 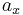$a_x$ bei der Projektion des Vektors $\vec{\textbf{a}}$ auf die parallel zum Einheitsvektor 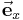$\vec{\textbf{e}}_{x}$ verlaufende Linie ergibt) lässt sich dieser Zusammenhang dann wie folgt ausdrücken:

$\vec{\textbf{a}} \cdot \vec{\textbf{e}}_{x} = |\vec{\textbf{a}}| |\vec{\textbf{e}}_{x}| \cos(\alpha) = a \cos(\alpha) = a_x$

Folglich können die Komponenten eines Vektors einfach dadurch bestimmt werden, dass man das Skalarprodukt aus diesem Vektor und den jeweils zugehörigen Einheitsvektoren bildet:

$\vec{\textbf{a}} = \vec{\textbf{e}}_x a_x + \vec{\textbf{e}}_y a_y + \vec{\textbf{e}}_z a_z = \vec{\textbf{e}}_x \left( \vec{\textbf{a}} \cdot \vec{\textbf{e}}_x \right) + \vec{\textbf{e}}_y \left( \vec{\textbf{a}} \cdot \vec{\textbf{e}}_y \right) + \vec{\textbf{e}}_z \left( \vec{\textbf{a}} \cdot \vec{\textbf{e}}_z \right)$

Komponentendarstellung von Vektorbeziehungen

Betrachtet man nun noch mal die verschiedenen Vektorbeziehungen, so lassen sich diese in Komponentendarstellung wie folgt angeben:

Addition und Subtraktion von Vektoren

$\vec{\textbf{a}} \pm \vec{\textbf{b}} = \vec{\textbf{e}}_x \left( a_x \pm b_x \right) + \vec{\textbf{e}}_y \left( a_y \pm b_y \right) + \vec{\textbf{e}}_z \left( a_z \pm b_z \right)$

Multiplikation eines Vektors mit einem Skalar

$\lambda \vec{\textbf{a}} = \vec{\textbf{e}}_x \lambda a_x + \vec{\textbf{e}}_y \lambda a_y + \vec{\textbf{e}}_z \lambda a_z$

Skalarprodukt

$\vec{\textbf{a}} \cdot \vec{\textbf{b}} = \left( \vec{\textbf{e}}_x a_x + \vec{\textbf{e}}_y a_y + \vec{\textbf{e}}_z a_z \right) \cdot \left( \vec{\textbf{e}}_x b_x + \vec{\textbf{e}}_y b_y + \vec{\textbf{e}}_z b_z \right) = a_x b_x + a_y b_y + a_z b_z$

Bildet man das Skalarprodukt zweier gleicher Vektoren, so ergibt sich der folgende Sonderfall:

$\vec{\textbf{a}} \cdot \vec{\textbf{a}} = \left| \vec{\textbf{a}} \right|^2 = a^2 = a^2_x + a^2_y + a^2_z$

Der Betrag von $\vec{\textbf{a}}$ lässt sich also auch dadurch bestimmen, dass man die Wurzel aus dem Skalarprodukt bildet:

$a = |\vec{\textbf{a}}| = \sqrt{\vec{\textbf{a}} \cdot \vec{\textbf{a}}}$

Vektorprodukt

$\begin{align} \vec{\textbf{a}} \times \vec{\textbf{b}} & = \left( \vec{\textbf{e}}_x a_x + \vec{\textbf{e}}_y a_y + \vec{\textbf{e}}_z a_z \right) \times \left( \vec{\textbf{e}}_x b_x + \vec{\textbf{e}}_y b_y + \vec{\textbf{e}}_z b_z \right)\\ & = a_x b_x \underbrace{\left( \vec{\textbf{e}}_x \times \vec{\textbf{e}}_x \right)}_{\vec{\textbf{0}}} + a_y b_x \underbrace{\left( \vec{\textbf{e}}_y \times \vec{\textbf{e}}_x \right)}_{-\vec{\textbf{e}}_z} a_z b_x \underbrace{\left( \vec{\textbf{e}}_z \times \vec{\textbf{e}}_x \right)}_{\vec{\textbf{e}}_y}\\ & + a_x b_y \underbrace{\left( \vec{\textbf{e}}_x \times \vec{\textbf{e}}_y \right)}_{\vec{\textbf{e}}_z} + a_y b_y \underbrace{\left( \vec{\textbf{e}}_y \times \vec{\textbf{e}}_y \right)}_{\vec{\textbf{0}}} a_z b_y \underbrace{\left( \vec{\textbf{e}}_z \times \vec{\textbf{e}}_y \right)}_{-\vec{\textbf{e}}_x}\\ & + a_x b_z \underbrace{\left( \vec{\textbf{e}}_x \times \vec{\textbf{e}}_z \right)}_{-\vec{\textbf{e}}_y} + a_y b_z \underbrace{\left( \vec{\textbf{e}}_y \times \vec{\textbf{e}}_z \right)}_{\vec{\textbf{e}}_x} a_z b_z \underbrace{\left( \vec{\textbf{e}}_z \times \vec{\textbf{e}}_z \right)}_{\vec{\textbf{0}}}\\ & = \vec{\textbf{e}}_x \left( a_y b_z - a_z b_y \right) + \vec{\textbf{e}}_y \left( a_z b_x - a_x b_z \right) + \vec{\textbf{e}}_z \left( a_x b_y - a_y b_x \right) \end{align}$

Literatur

• Anthony Croft und Robert Davison, Mathematics for Engineers: a modern interactive approach, 3. Auflage (Pearson-Prentice Hall, 2008)
• Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)