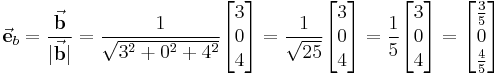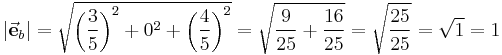Einheitsvektoren
| ← Zurück: Einführung in die Vektorrechnung | Übersicht: Vektorrechnung | Vorwärts: Einfache Rechenoperationen mit Vektoren → |
|
Zu diesem Thema stehen Aufgaben zur Selbstkontrolle zur Verfügung. |
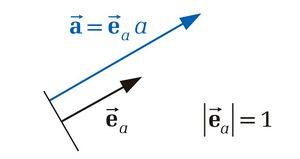
Unter einem Einheitsvektor versteht man allgemein einen Vektor mit dem Betrag beziehungsweise der Länge 1. Der Einheitsvektor 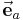 zu einem gegebenen Vektor
zu einem gegebenen Vektor  lässt sich dadurch bestimmen, dass man den gegebenen Vektor durch seinen Betrag
lässt sich dadurch bestimmen, dass man den gegebenen Vektor durch seinen Betrag 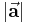 dividiert:
dividiert:
Der Vektor 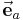 hat die Länge 1 (es gilt also
hat die Länge 1 (es gilt also 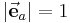 ) und zeigt in Richtung des Vektors
) und zeigt in Richtung des Vektors  . Auf diese Weise lässt sich jeder Vektor als Produkt aus seinem Betrag (also einer skalarwertigen Größe) und dem dazugehörigen Einheitsvektor angeben. Der Vektor
. Auf diese Weise lässt sich jeder Vektor als Produkt aus seinem Betrag (also einer skalarwertigen Größe) und dem dazugehörigen Einheitsvektor angeben. Der Vektor  kann somit auch wie folgt dargestellt werden:
kann somit auch wie folgt dargestellt werden:
Beobachtet man die Wirkung von Ladungen aufeinander, so lässt sich feststellen, dass diese Kräfte aufeinander ausüben. Werden nun zwei Punktladungen Bei der Kraft handelt es sich um eine gerichtete und damit vektorielle Größe, die in diesem Fall ausschließlich vom Abstand der Ladungen abhängt. In der Gleichung fehlt aber noch die Richtungsinformation über die Kraftwirkung. Diese muss in der Gleichung derart berücksichtigt werden, dass sich der Betrag der Kraft nicht ändert. Zu diesem Zweck kann ein Einheitsvektor Damit kann die Gleichung für die Coulombkraft in vektorieller Form wie folgt angegeben werden: Zur Verdeutlichung dieser Zusammenhänge steht ein Applet zur Verfügung. |
Gegeben ist der Vektor Das dieser Vektor tatsächlich die Länge 1 hat, lässt sich leicht durch die Bestimmung des Betrags überprüfen: |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Wolfgang Pavel und Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
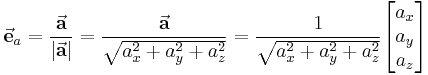
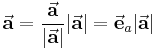
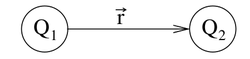
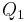 und
und 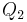 im Abstand
im Abstand 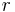 zueinander positioniert (siehe Abbildung), so herrscht zwischen ihnen eine Kraft
zueinander positioniert (siehe Abbildung), so herrscht zwischen ihnen eine Kraft 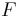 gemäß dem Coulombschen Gesetz:
gemäß dem Coulombschen Gesetz:
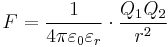
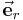 in Richtung des Abstandsvektors
in Richtung des Abstandsvektors 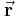 eingeführt werden, der diese Information angibt:
eingeführt werden, der diese Information angibt:
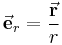
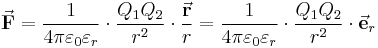
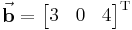 (das
(das 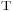 steht für
steht für