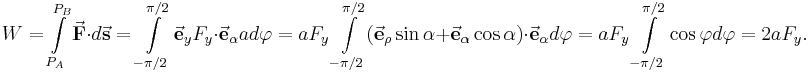Das Linienintegral: Unterschied zwischen den Versionen
| Zeile 76: | Zeile 76: | ||
Damit folgt für das Linienintegral: | Damit folgt für das Linienintegral: | ||
:<math> | :<math> | ||
| − | \int\limits_{P_A}^{P_B}\vec{E}\cdot \mathrm{d}\vec{\textbf{s}} = \lim_{n\to\infty,\,\Delta s_i \to 0}\sum_{i=1}^n \left|\vec{\textbf{E}}(x_i, y_i, z_i)\right|\left|\Delta\vec{\textbf{s}}_i\right|\cos(\alpha_i) | + | \int\limits_{P_A}^{P_B}\vec{\textbf{E}}\cdot \mathrm{d}\vec{\textbf{s}} = \lim_{n\to\infty,\,\Delta s_i \to 0}\sum_{i=1}^n \left|\vec{\textbf{E}}(x_i, y_i, z_i)\right|\left|\Delta\vec{\textbf{s}}_i\right|\cos(\alpha_i) |
</math> | </math> | ||
Version vom 30. August 2012, 19:57 Uhr
To-do:
- Einleitung etwas plausibler (es gibt doch genügend Beispiele)
- Formulierungen überarbeiten (insbes. fett)
- Grafik Spannungsberechnung in einem homogenen elektrischen Feld: Größe, Richtung von phi fehlt
- In der Einleitung sollte auf die Unterabschnitte verwiesen werden
- Das Erscheinungsbild dieser Seite ist nicht zufriedenstellend -> zu unübersichtlich, zu viel Inhalt
- Irgendwo sollte etwas zu den Namen stehen (Linien = Kurvenintegrale)
Inhaltsverzeichnis
Das Linienintegral einer skalaren Größe
Das Linien- oder Kurvenintegral beschreibt eine Integration entlang einer (gerichteten) Kontur 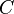 , z. B. von einem Anfangspunkt
, z. B. von einem Anfangspunkt 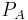 bis zu einem Endpunkt
bis zu einem Endpunkt 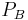 . Dabei gibt es nur eine Integrationsvariable. Bei einer Integration entlang der
. Dabei gibt es nur eine Integrationsvariable. Bei einer Integration entlang der  -Achse ist das zugehörige Differential beispielsweise durch
-Achse ist das zugehörige Differential beispielsweise durch 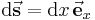 gegeben. Handelt es sich bei dem Integrationsweg
gegeben. Handelt es sich bei dem Integrationsweg  um eine geschlossene Kontur, d. h. der Anfangs- und Endpunkt fallen zusammen
um eine geschlossene Kontur, d. h. der Anfangs- und Endpunkt fallen zusammen  , wird das Linienintegral als Ring- oder Umlaufintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
, wird das Linienintegral als Ring- oder Umlaufintegral bezeichnet und das Integralzeichen wird mit einem Ring dargestellt.
Das Linienintegral wird benötigt, wenn eine (ggf. vektorielle) Funktion von mehreren Variablen abhängt und entlang einer (im Allgemeinen nicht geradlinigen) Kontur zu integrieren ist. Dies ist zum Beispiel beim Durchflutungsgesetz (vgl. Erweiterung der Integralrechnung:Übersicht) der Fall. Prinzipiell handelt es sich um eine Erweiterung der Integralrechnung mit einer skalaren Funktion und nur einer Integrationsvariablen.
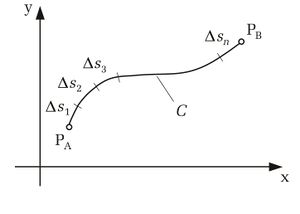
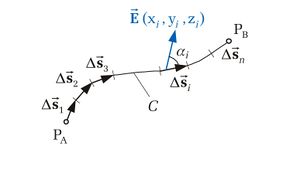
Zur Herleitung des Linienintegrals wird exemplarisch eine von zwei Variablen abhängige Funktion 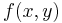 betrachtet, die entlang einer Kurve zwischen den Punkten
betrachtet, die entlang einer Kurve zwischen den Punkten  und
und 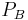 integriert werden soll (siehe Abbildung). Hierzu wird die Kontur zunächst in
integriert werden soll (siehe Abbildung). Hierzu wird die Kontur zunächst in 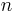 Teilstücke zerlegt. Dabei wird die Länge des
Teilstücke zerlegt. Dabei wird die Länge des 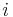 -ten Teilstücks mit
-ten Teilstücks mit 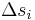 bezeichnet. Auf einem solchen
bezeichnet. Auf einem solchen 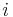 -ten Teilstück kann der jeweilige Funktionswert
-ten Teilstück kann der jeweilige Funktionswert 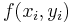 als näherungsweise konstant angenommen werden. Dadurch lässt sich ein Näherungswert für das Linienintegral dadurch angeben, dass die Produkte der Funktionswerte mit den Längen der Teilstücke aufsummiert werden:
als näherungsweise konstant angenommen werden. Dadurch lässt sich ein Näherungswert für das Linienintegral dadurch angeben, dass die Produkte der Funktionswerte mit den Längen der Teilstücke aufsummiert werden:
Es wurde bereits beschrieben, dass die Funktionswerte 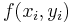 auf den Teilstücken als näherungsweise konstant angenommen werden können. Die Näherung ist dabei umso genauer, je kleiner die Teilstücke gewählt werden. Daher wird zu infinitesimal kleinen Teilstücken (
auf den Teilstücken als näherungsweise konstant angenommen werden können. Die Näherung ist dabei umso genauer, je kleiner die Teilstücke gewählt werden. Daher wird zu infinitesimal kleinen Teilstücken (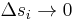 ) übergangen, von denen es dann unendlich viele gibt (
) übergangen, von denen es dann unendlich viele gibt (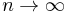 ). Auf diese Weise erhält man das entsprechende Linienintegral:
). Auf diese Weise erhält man das entsprechende Linienintegral:
Für eine möglichst einfache Lösung der Integrale bietet sich die Verwendung eines auf den jeweiligen Anwendungsfall „zugeschnittenen“ Koordinatensystems an.
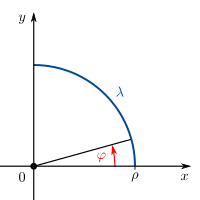
In diesem Beispiel werden verschiedene Fälle einer gegebenen Linienladung betrachtet. Bei einer Linienladung handelt es sich um eine Ladungsanordnung entlang einer Kontur. Dabei gibt die Linienladungsdichte Fall 1: Konstante und geradlinig angeordnete Linienladung Bei einer konstanten und entlang der Aufgrund der konstanten Linienladungsdichte kann die Gesamtladung folglich auch sofort ohne die Integration angegeben werden. Fall 2: Ortsabhängige und geradlinig angeordnete Linienladung Handelt es sich bei der Linienladungsdichte um eine ortsabhängige Größe, so kann das Ergebnis nicht einfach durch die Multiplikation dieser Größe mit der Strecke angegeben werden. Betrachtet wird zum Beispiel eine linear zunehmende Linienladungsdichte: Dabei ist Fall 3: Konstante und krummlinig angeordnete Linienladung In diesem Fall wird eine Linienladung in Form eines Viertelkreisbogens betrachtet. Da die Linienladungsdichte wieder konstant ist, muss diese zur Bestimmung der Gesamtladung lediglich mit der Länge dieses Viertelkreisbogens multipliziert werden. Dazu ist ein Übergang zu den Zylinderkoordinaten zweckmäßig. Mit Das verwendete Integral dient der Anschauung, alternativ kann die Länge des Viertelkreisbogens auch direkt als ein Viertel des Kreisumfangs angegeben werden. |
Das Linienintegral einer vektoriellen Größe
Linienintegrale treten häufig auch in vektorieller Form auf. Dabei ist eine vektorielle Funktion, z. B. 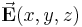 , entlang einer ebenfalls gerichteten Kontur mit den Wegelementen
, entlang einer ebenfalls gerichteten Kontur mit den Wegelementen 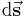 zu integrieren. Im Vergleich zum skalarwertigen Linienintegral ist also zusätzlich das Skalarprodukt
zu integrieren. Im Vergleich zum skalarwertigen Linienintegral ist also zusätzlich das Skalarprodukt 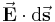 für jedes Wegelement
für jedes Wegelement 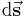 zu bestimmen. Aufgrund der Projektionseigenschaft das Skalarprodukts wird nur die jeweils tangential zum Wegelement verlaufende Kompotente des Vektors
zu bestimmen. Aufgrund der Projektionseigenschaft das Skalarprodukts wird nur die jeweils tangential zum Wegelement verlaufende Kompotente des Vektors 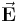 integriert. Für die weitere Herleitung wird ansonsten wie im skalarwertigen Fall verfahren.
integriert. Für die weitere Herleitung wird ansonsten wie im skalarwertigen Fall verfahren.
Die Kontur wird nun in 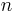 vektorielle Teilstücke zerlegt, wobei das
vektorielle Teilstücke zerlegt, wobei das 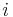 -te Teilelement mit
-te Teilelement mit 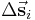 bezeichnet wird. Auf einem solchen <amth>i</math>-ten Teilstück kann der jeweilige Funktionswert
bezeichnet wird. Auf einem solchen <amth>i</math>-ten Teilstück kann der jeweilige Funktionswert 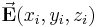 als näherungsweise konstant angenommen werden. Damit gilt für das Skalarprodukt bezogen auf das
als näherungsweise konstant angenommen werden. Damit gilt für das Skalarprodukt bezogen auf das 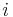 -te Teilstück:
-te Teilstück:
Damit folgt für das Linienintegral:
Spezialfälle beschreiben!!!
Im vorherigen ging es um die Integration skalarer Größen. Hat man aber beispielsweise ein elektrisches Feld 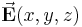 angelegt, betrachtet man nicht nur die Stärke, sondern auch die Richtung des Feldes im Raum. Um das berücksichtigen zu können, muss die Form des Linienintegrals angepasst werden. Deswegen hat man sowohl bei der Funktion
angelegt, betrachtet man nicht nur die Stärke, sondern auch die Richtung des Feldes im Raum. Um das berücksichtigen zu können, muss die Form des Linienintegrals angepasst werden. Deswegen hat man sowohl bei der Funktion 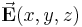 als auch bei dem Wegelement
als auch bei dem Wegelement 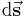 eine vektorielle Größe, da es in diesem Beispiel den Unterschied zwischen einer positiven, negativen oder gar keiner Spannung machen kann.
eine vektorielle Größe, da es in diesem Beispiel den Unterschied zwischen einer positiven, negativen oder gar keiner Spannung machen kann.
Zur Bestimmung des Linienintegrals einer vektoriellen Größe kann ebenso wie bei skalaren Größen das Integral über die infinitesimalen Wegelemente berechnet werden. Man verwendet nun wieder eine Kontur C, die zwischen den Punkten 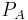 und
und 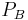 verläuft. Allerdings sind diesmal, die Wegelemente
verläuft. Allerdings sind diesmal, die Wegelemente 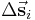 gerichtete Größen. Auch hier wird die Kontur in n Teilstücke
gerichtete Größen. Auch hier wird die Kontur in n Teilstücke 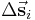 mit i = 1 ... n unterteilt und ein Punkt
mit i = 1 ... n unterteilt und ein Punkt 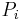 mit den Koordinaten
mit den Koordinaten 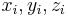 einer vektoriellen Größe
einer vektoriellen Größe 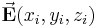 zugeordnet.
Um nun das Linienintegral berechnen zu können, muss das Skalarprodukt zwischen jedem Wegelement, dem dazugehörigen Funktionswert und dem eingeschlossenem Winkel
zugeordnet.
Um nun das Linienintegral berechnen zu können, muss das Skalarprodukt zwischen jedem Wegelement, dem dazugehörigen Funktionswert und dem eingeschlossenem Winkel 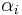 gebildet werden.
gebildet werden.
Summiert man nun ebenfalls alle Skalarprodukte auf und bildet gemäß der Gleichung des Linienintegrals der skalaren Größen den Grenzwert, erhält man für das Linienintegral einer vektoriellen Größe folgende Form:
Ein häufiger Anwendungsfall des Linienintegrals ergibt sich bei der Bestimmung der Spannung im elektrischen Feld.
Bildet man beispielsweise eine Kontur gemäß der Abbildung in einem homogenen, gleichgerichtetem elektrischen Feld erhält man folgendes Ringintegral:
Um dieses Integral zu lösen, können wir vier Fälle unterscheiden: Nun unterteilt man das Integral in diese vier Bereiche und bildet jeweils das Skalarprodukt: Daraus folgt: Durch die eingeschlossenen Rechten Winkel in zwei Fällen ergibt das Skalarprodukt Null und es bleibt nur noch übrig: Da hier die Strecken zwischen Dies ist eine wichtige Erkenntnis im elektrostatischen Feld: Das Ringintegral über ein homogenes, elektrisches Feld ergibt immer Null. |
Gesucht ist die Arbeit
die an einer Kugel verichtet wird, welche infolge einer Kraft Der Bewegungsvorgang wird im zylindrischen Koordinatensystem mit dem Ursprung im Mittelpunkt des Kreises beschrieben, dadurch bewegt sich die Kugel in Richtung wachsender Um die geleistete Arbeit W zu bestimmen, muss die Kraft in Komponenten zerlegt werden, da nur die in Richtung der Bewegung wirkende Kraftkomponente einen Beitrag zur Arbeit leistet. Eine Komponente wirkt in Richtung |
Multimediale Lehrmaterialien
|
http://www.dangries.com/Flash/IntegralSketch/IntegralSketch.html Applet zum Verständnis von Integralen http://www.uni-due.de/~matj00/bauws10/VorlBau100518.html Applet zum Verständnis von Integralen http://mathdl.maa.org/images/upload_library/4/vol4/kaskosz/antapp.html Applet: verschiedener Kurvenbeispiele und ihre Integrale (engl.) |
Hilfreiche Links
|
http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/integralfkt/integralfkt1.html Interaktives Arbeitsblatt zur Integration http://web.mit.edu/8.02t/www/materials/modules/ReviewB.pdf Bebilderte Erklärung zu Kartesischen-, Kugel-, und Zylinderkoordinatensystemen und deren infinitesimalen Elementen (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Hempel, "Mathematische Grundlagen", Linienintegral, Universität Magdeburg
- TU Freiberg, "Parameter- und Kurvenintegrale", Script, 2010
| ← Zurück: Erweiterung der Integralrechnung:Übersicht | Übersicht: Erweiterung der Integralrechnung | Vorwärts: Das Flächenintegral → |
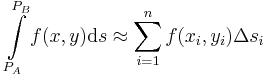
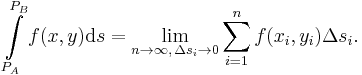
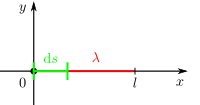
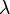 die Ladungsmenge pro Streckenabschnitt an. Um die gesamte Ladung entlang einer Kontur berechnen zu können, muss die Linienladungsdichte entlang der jeweiligen Kontur integriert werden:
die Ladungsmenge pro Streckenabschnitt an. Um die gesamte Ladung entlang einer Kontur berechnen zu können, muss die Linienladungsdichte entlang der jeweiligen Kontur integriert werden:
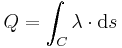
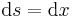 (vgl.
(vgl. 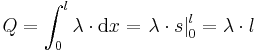

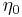 eine Konstante mit der Einheit
eine Konstante mit der Einheit 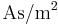 (ansonsten hätte
(ansonsten hätte 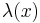 keine zu einer Linienladungsdichte passende Einheit
keine zu einer Linienladungsdichte passende Einheit 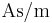 ). Die Linienladungsdichte wird also entlang der
). Die Linienladungsdichte wird also entlang der 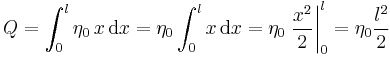
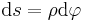 (vgl.
(vgl. 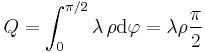
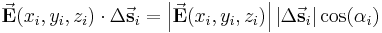
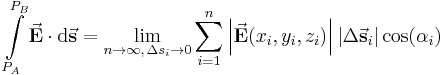
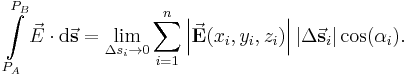
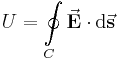

 bis
bis  , die mit dem Elektrischen Feld verläuft.
, die mit dem Elektrischen Feld verläuft. bis
bis  , die entgegen dem Elektrischen Feld verläuft.
, die entgegen dem Elektrischen Feld verläuft.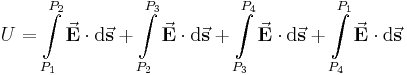
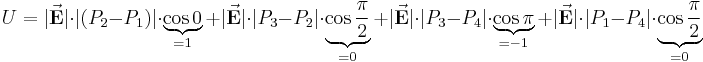
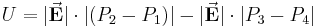
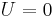
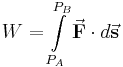 ,
,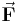 eine Laufrinne hinunterrollt. Die Laufrinne ist halbkreisförmig und spannt sich vom Anfangspunkt
eine Laufrinne hinunterrollt. Die Laufrinne ist halbkreisförmig und spannt sich vom Anfangspunkt 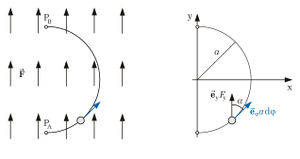
 -Werte auf einem Halbkreis mit konstantem Radius
-Werte auf einem Halbkreis mit konstantem Radius 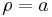 . So ist auf dem Halbkreis der Winkel
. So ist auf dem Halbkreis der Winkel 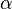 zwischen der Bewegungsrichtung
zwischen der Bewegungsrichtung 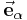 und der Kraftrichtung
und der Kraftrichtung 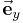 bekannt, da die vorgegebene Kraft sich am einfachsten mit einer kartesischen Komponente
bekannt, da die vorgegebene Kraft sich am einfachsten mit einer kartesischen Komponente 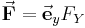 beschreiben lässt.
beschreiben lässt.
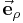 .
Nun benötigt man das Skalarprodukt aus der vektoriellen Kraft und dem gerichteten Wegelement, dessen Integration vom Anfangspunkt
.
Nun benötigt man das Skalarprodukt aus der vektoriellen Kraft und dem gerichteten Wegelement, dessen Integration vom Anfangspunkt