Transformations
| ← Back: Adjugate Formula | Overview: Transformations | Next: Translation → |
In this article general transformations used in the context of robotics and the underlying mathematics are described.
In the robotics field and especially in the course "Robotics" of the University of Paderborn, Cartesian coordinates are used. Cartesian coordinate systems are always orthogonal systems following the right hand rule shown in the figure on the right. So if you hold your hand accordingly, the thumb points in the direction of the 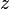 -axis, the index finger in the direction of the
-axis, the index finger in the direction of the 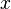 -axis and the middle finger is directed orthogonal to the two others along the
-axis and the middle finger is directed orthogonal to the two others along the 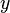 -axis.
-axis.
Transformations are applied to vectors or coordinates in vector notation, respectively. All types of transformations can be achieved by matrix multiplication. To transform a vector 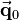 to
to 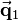 ,
, 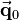 has to be multilplied by the transformation matrix
has to be multilplied by the transformation matrix 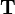 :
:
The basic transformation matrix is an identity matrix, which corresponds to an empty transformation. So an identity matrix as transformation matrix always results in the original vector. The following equation shows this for three dimensions, but it also holds for two, four and more dimensions:
By modifying the components of the transformation matrix different types of transformations can be achieved. In n-dimensional space rotation can basically be described by an n-by-n transformation matrix. Translation however is actually a vector addition with an n-by-1 vector. So first the two basic types of transformations are explained individually. Then homogeneous coordinates are introduced to be able to apply all kinds of transformations by matrix multiplication and it is explained how transformations are combined. Conclusively the last subarticle presents a special matrix inversion method for inverse transformations.
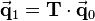
![\vec{\mathbf{q}}_1=\mathbf{I}_3\cdot\vec{\mathbf{q}}_0=
\left[\begin{array}{ccc}
1&0&0\\
0&1&0\\
0&0&1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0\\
y_0\\
z_0
\end{array}\right]=
\left[\begin{array}{c}
1\cdot x_0+0\cdot y_0+0\cdot z_0\\
0\cdot y_0+1\cdot y_0+0\cdot z_0\\
0\cdot y_0+0\cdot y_0+1\cdot z_0
\end{array}\right]=
\left[\begin{array}{c}
x_0\\
y_0\\
z_0
\end{array}\right]=
\vec{\mathbf{q}}_0](/wiki/robotics/images/math/7/1/e/71ecdb2116e3db5f045c9dbf77c97b97.png)