Combinations of transformations
| ← Back: Homogeneous coordinates | Overview: Transformations | Next: Inverse transformation → |
In the previous subarticle homogeneous coordinates and transformation matrices for translation and rotation around the three axes are introduced:
These transformation matrices can be combined by multiplying them.
Consider the following transformation matrix 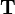 that corresponds to the multiplication of several single transformation matrices (also denoted with
that corresponds to the multiplication of several single transformation matrices (also denoted with 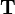 for simplification):
for simplification):
Combinations of transformations are always applied from right to left. So in the example case, 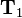 is applied first. Then on this result, transformation
is applied first. Then on this result, transformation 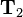 is applied and so on. The left transformation matrix
is applied and so on. The left transformation matrix 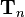 is finally multiplied with the result of all the previous transformations.
is finally multiplied with the result of all the previous transformations.
As already stated for multiplication of matrices, different multiplication orders lead to different results. If only translations are regarded, the order does not matter, because translation is actually vector addition and vector addition is commutative. Rotation however depends on the current input coordinates. Descriptively seen, rotation is always applied around the origin of the global coordinate system or around an axis intersecting with the origin, respectively. So the rotational part is depending on the respective current coordinates. Different orders of transformations result in different input coordinates for each transformation.
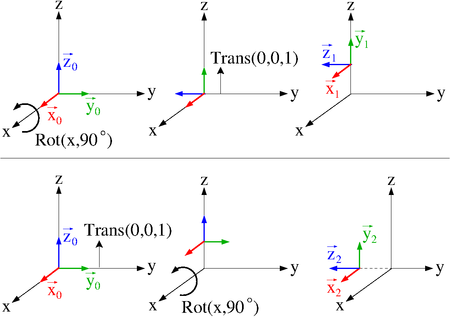
The following example shows descriptively as well as computationally, that the order of transformations is important (see figure on the right). Consider a local coordinate frame positioned in the origin, whose axes are oriented parallel to the global coordinate axes. The related initial position vector 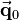 is a zero vector. A translation matrix
is a zero vector. A translation matrix 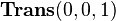 and a rotation matrix
and a rotation matrix 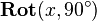 are to be applied to this local frame. So two different orders of the two transformations are possible.
are to be applied to this local frame. So two different orders of the two transformations are possible.
The upper three subfigures on the right show the first case. The local frame is first rotated around the x-axis and then translated on the z-axis. The result is shown in the top right subfigure. Computationally 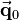 is first pre-multiplied with
is first pre-multiplied with 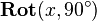 and then pre-multiplied with
and then pre-multiplied with 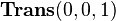 :
:
The lower three subfigures on the right show the second case. The local frame is first translated on the z-axis and then rotated around the x-axis. The result is shown in the lower right subfigure. Computationally 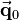 is first pre-multiplied with
is first pre-multiplied with 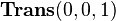 and then pre-multiplied with
and then pre-multiplied with 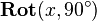 :
:
As you can see from the transformed vectors 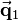 and
and 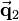 , the transformation order influences the result. In the example there is only one rotation applied. So the orientation of the local frame is the same in both cases. But if there is more than one rotation applied, the resulting orientation differs as well.
, the transformation order influences the result. In the example there is only one rotation applied. So the orientation of the local frame is the same in both cases. But if there is more than one rotation applied, the resulting orientation differs as well.
The general homogeneous transformation matrix 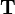 , introduced for homogeneous coordinates, consists of a rotation matrix and a translation vector. As shown in the subarticle, multiplication of
, introduced for homogeneous coordinates, consists of a rotation matrix and a translation vector. As shown in the subarticle, multiplication of 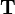 with a vector corresponds to rotating the coordinates first and then adding the translation vector. Written as product of homogeneous transformation matrices,
with a vector corresponds to rotating the coordinates first and then adding the translation vector. Written as product of homogeneous transformation matrices, 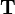 equals: (where axis is either
equals: (where axis is either 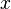 ,
,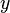 or
or 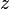 )
)
As explained for Homogeneous coordinates applying a homogeneous transformation matrix 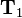 is equivalent to first multiplying with the corresponding rotation matrix and then adding the translation vector:
is equivalent to first multiplying with the corresponding rotation matrix and then adding the translation vector:
Assume the composed transformation 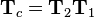 . So
. So 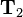 is to be applied on the result of the first transformation, which leads to:
is to be applied on the result of the first transformation, which leads to:
Thus the multiplication of two general homogeneous transformation matrices is defined as follows:
Applet
The following applet can be used to test some combinations of different transformations and see the results in a three-dimensional visualization.
This example is taken from pages 3-34 and 3-35 of the robotics script. The transformation
When The four transformation matrices are multiplied to obtain the combined transformation matrix (for further intermediate steps have a look in the script on page 3-35): The above combined matrix corresponds to the four single transformation steps applied in the designated order. As can be seen in the lower right subfigure, the resulting coordinates of the local frame correspond to the translation vector |
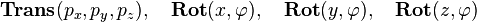
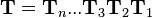
![\begin{align}
\vec{\mathbf{q}}_1&=
\left[\begin{array}{c}
x_1\\
y_1\\
z_1\\
1
\end{array}\right]=
\mathbf{Trans}(0,0,1)\mathbf{Rot}(x,90^\circ)\vec{\mathbf{q}}_0 =
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{c}
x_0\\
y_0\\
z_0\\
1
\end{array}\right] \\ &=
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 1 & 0 & 1\\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{c}
x_0\\
y_0\\
z_0\\
1
\end{array}\right]=
\left[\begin{array}{c}
x_0\\
-z_0\\
y_0+1\\
1
\end{array}\right]=
\left[\begin{array}{c}
0\\
0\\
1\\
1
\end{array}\right]
\end{align}](/wiki/robotics/images/math/d/6/4/d64e5d3d8993b7f423bc53d105cb46c6.png)
![\begin{align}
\vec{\mathbf{q}}_2&=
\left[\begin{array}{c}
x_2\\
y_2\\
z_2\\
1
\end{array}\right]=
\mathbf{Rot}(x,90^\circ)\mathbf{Trans}(0,0,1)\vec{\mathbf{q}}_0 =
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{c}
x_0\\
y_0\\
z_0\\
1
\end{array}\right] \\ &=
\left[\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 0 & -1 & -1\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{c}
x_0\\
y_0\\
z_0\\
1
\end{array}\right]=
\left[\begin{array}{c}
x_0\\
-z_0-1\\
y_0\\
1
\end{array}\right]=
\left[\begin{array}{c}
0\\
-1\\
0\\
1
\end{array}\right]
\end{align}](/wiki/robotics/images/math/4/9/a/49a33b764d8a5baf3a05d40327192cf2.png)
![\mathbf{T}=
\left[\begin{array}{ccc|c}
& & & \\
& \mathbf{R} & & \vec{\mathbf{p}}\\
& & & \\ \hline
0 & 0 & 0 & 1
\end{array}\right]=
\mathbf{Trans}(p_x,p_y,p_z)\mathbf{Rot}(axis,\varphi)](/wiki/robotics/images/math/9/6/0/960af1d9d4d8d934ffbacb93a67d9409.png)
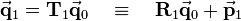
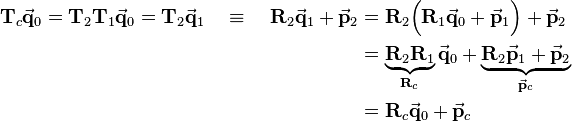
![\begin{align}
\mathbf{T}_c = \mathbf{T}_2\mathbf{T}_1 &= \left[\begin{array}{cccc} & & & \\ & \mathbf{R}_2 & & \vec{\mathbf{p}}_2 \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_1 & & \vec{\mathbf{p}}_1 \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right] \\
&=
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_2\mathbf{R}_1 & & \mathbf{R}_2\vec{\mathbf{p}}_1+\vec{\mathbf{p}}_2 \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
\end{align}](/wiki/robotics/images/math/a/4/d/a4dc76ca2ca7b39291e9acf1235783d0.png)
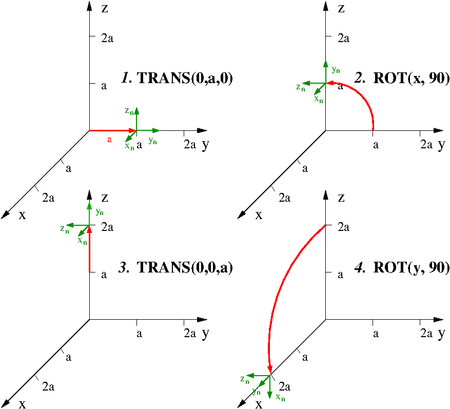
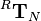 of the object frame
of the object frame 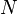 with respect to the reference frame
with respect to the reference frame 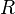 is defined as follows:
is defined as follows: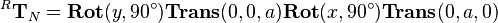
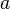 along the y-axis and then rotated by 90 degrees around the x-axis. Then again a translation by
along the y-axis and then rotated by 90 degrees around the x-axis. Then again a translation by ![\begin{align}
^R\mathbf{T}_N &=
\mathbf{Rot}(y,90^\circ)\mathbf{Trans}(0,0,a)\mathbf{Rot}(x,90^\circ)\mathbf{Trans}(0,a,0)\\
&=
\left[\begin{array}{cccc}
\cos90^\circ & 0 & \sin90^\circ & 0 \\
0 & 1 & 0 & 0 \\
-\sin90^\circ & 0 & \cos90^\circ & 0 \\
0 & 0 & 0 & 1 \\
\end{array}\right]
\cdot
\left[
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & a \\
0 & 0 & 0 & 1\\
\end{array}
\right]
\cdot
\left[
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & \cos90^\circ & -\sin90^\circ & 0 \\
0 & \sin90^\circ & ~\cos90^\circ & 0 \\
0 & 0 & 0 & 1 \\
\end{array}
\right]
\left[
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & a \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}
\right]\\
\\
&= ... \qquad \text{(page 3-35 in the script)}\\
\\
&=
\left[\begin{array}{cccc}
~~0 & 1 &~~0 &~2a \\
~~0 & 0 & -1 &~~0 \\
-1 & 0 &~~0 &~~0 \\
~~0 & 0 &~~0 &~~1 \\
\end{array}\right]\\
&=
\left[\begin{array}{cccc}
\vec{\mathbf{x}} & \vec{\mathbf{y}} & \vec{\mathbf{z}} & \vec{\mathbf{p}}\\
0 & 0 & 0 & 1 \\
\end{array}\right]
\end{align}](/wiki/robotics/images/math/3/d/4/3d4d6162a39ea3fbb135313e516acb86.png)
![\vec{\mathbf{p}}=[2a,0,0]^T](/wiki/robotics/images/math/1/9/7/197d8b8356fb3ba672e28679b8698a57.png) within the combined matrix. The axes of the coordinate frame are oriented like the vectors
within the combined matrix. The axes of the coordinate frame are oriented like the vectors 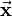 ,
, 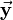 and
and 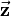 within the matrix.
within the matrix.