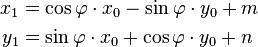Multiplication of matrices
| ← Back: Addition of matrices | Overview: Matrices | Next: Determinant of a matrix → |
|
There are exercises as selftest for this article. |
Two matrices can be multiplied if the number of colums of the left matrix equals the number of rows of the right matrix. The result of the multiplication of an l-by-m matrix  with an m-by-n matrix
with an m-by-n matrix 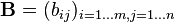 is an l-by-n matrix
is an l-by-n matrix 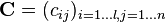 . To calculate the components of the resulting matrix, the components of one row of the first matrix are multiplied with the components of one column of the second matrix respectively and summed up. For example for the component
. To calculate the components of the resulting matrix, the components of one row of the first matrix are multiplied with the components of one column of the second matrix respectively and summed up. For example for the component  the components of row
the components of row 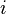 of the first matrix are multiplied with the components of column
of the first matrix are multiplied with the components of column 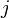 of the second matrix. This leads to the following equation for the components of
of the second matrix. This leads to the following equation for the components of 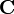 :
:
A clear possibility to compute the resulting matrix is the pattern of Falk. Thereto the first matrix 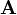 is noted and on the right over it the second matrix
is noted and on the right over it the second matrix 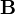 . Then the row vectors of
. Then the row vectors of 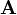 and the column vectors of
and the column vectors of 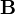 lead to l times n intersections which correspond to the l-by-n result matrix
lead to l times n intersections which correspond to the l-by-n result matrix 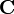 . The l times n components are determined by computing the dot product of the crossing row vector of
. The l times n components are determined by computing the dot product of the crossing row vector of 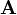 and column vector of
and column vector of 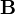 :
:
For example the multiplication of a 2-by-3 matrix with a 3-by-2 matrix results in a 2-by-2 matrix and is computed as follows:
As it holds that 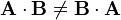 , the order of a matrix product is important. To specify the order, two types of multiplication are distinguished, pre- and post-multiplication. Pre-multiplying a matrix
, the order of a matrix product is important. To specify the order, two types of multiplication are distinguished, pre- and post-multiplication. Pre-multiplying a matrix 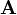 by matrix
by matrix 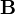 means, that
means, that 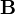 is written on the left side of the matrix product:
is written on the left side of the matrix product: 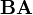 . If matrix
. If matrix 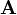 is post-multiplied by matrix
is post-multiplied by matrix 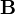 ,
,  is written on the right side:
is written on the right side:  .
.
Some further rules for matrix multiplications are:
A good example for the multiplication of several matrices in the context of robotics and transformations is presented in the robotics script. Please have a look in chapter 3 on page 3-35 |
Multiplication of matrices with vectors
A vector is a just special form of a matrix with either only one row or one column. Because an l-by-m matrix can only be multiplied by an m-by-n matrix, there are two possibilities of multiplying matrices and vectors. The first possibility is a 1-by-m row vector multiplied with an m-by-n matrix which results in a 1-by-n row vector:
The second possibility is a l-by-m matrix multiplied with an m-by-1 column vector which results in a l-by-1 column vector:
In chapter 3 of the robotics script some examples of matrices multiplied with vectors appear. On page 3-28 a two-dimensional transformation equation is presented for a rotation about This means that the new coordinates |
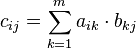

![\mathbf{A}\cdot\mathbf{B}=
\left[\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}
\end{array}\right]\cdot
\left[\begin{array}{cc}
b_{11} & b_{12} \\
b_{21} & b_{22}\\
b_{31} & b_{32}
\end{array}\right]=
\left[\begin{array}{cc}
a_{11}\cdot b_{11}+a_{12}\cdot b_{21}+a_{13}\cdot b_{31} & a_{11}\cdot b_{12}+a_{12}\cdot b_{22}+a_{13}\cdot b_{12} \\
a_{21}\cdot b_{11}+a_{22}\cdot b_{21}+a_{23}\cdot b_{31} & a_{21}\cdot b_{12}+a_{22}\cdot b_{22}+a_{23}\cdot b_{12}
\end{array}\right]](/wiki/robotics/images/math/a/6/0/a60eb4b58962ac775002fcbe9dace286.png)
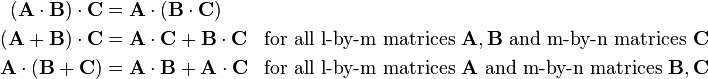
![\left[\begin{array}{ccc}
v_{11} & \dots & v_{1m}
\end{array}\right]
\cdot
\left[\begin{array}{ccc}
a_{11} & \dots & a_{1n}\\
\vdots & \ddots & \vdots\\
a_{m1} & \dots & a_{mn}
\end{array}\right]
=
\left[\begin{array}{ccc}
v_{11}a_{11}+\dots+v_{1m}a_{m1} & \dots & v_{11}a_{1n}+\dots+v_{1m}a_{mn}
\end{array}\right]](/wiki/robotics/images/math/1/9/7/197e995ca2b28be108faa7a88459bc18.png)
![\left[\begin{array}{ccc}
a_{11} & \dots & a_{1m}\\
\vdots & \ddots & \vdots\\
a_{l1} & \dots & a_{lm}
\end{array}\right]
\cdot
\left[\begin{array}{c}
v_{11}\\
\vdots \\
v_{m1}
\end{array}\right]
=
\left[\begin{array}{c}
a_{11}v_{11}+\dots+a_{1m}v_{m1}\\
\vdots \\
a_{l1}v_{11}+\dots+a_{lm}v_{m1}
\end{array}\right]](/wiki/robotics/images/math/8/5/d/85d25eb1c5233458e22b6f99c91978bc.png)

 about the origin (see figure) in combination with a translation. The equation uses
about the origin (see figure) in combination with a translation. The equation uses ![\left[\begin{array}{c}
x_1 \\
y_1 \\
1
\end{array}\right]=
\left[\begin{array}{ccc}
\cos\varphi & -\sin\varphi & m\\
\sin\varphi & \cos\varphi & n\\
0 & 0 & 1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0 \\
y_0 \\
1
\end{array}\right] =
\left[\begin{array}{c}
\cos\varphi\cdot x_0-\sin\varphi\cdot y_0+m\\
\sin\varphi\cdot x_0+\cos\varphi\cdot y_0+n\\
0\cdot x_0+0\cdot y_0+1\cdot 1
\end{array}\right]=
\left[\begin{array}{c}
\cos\varphi\cdot x_0-\sin\varphi\cdot y_0+m\\
\sin\varphi\cdot x_0+\cos\varphi\cdot y_0+n\\
1
\end{array}\right]](/wiki/robotics/images/math/e/6/b/e6bebf6a1f6e5aead20a58c345e4f50c.png)
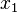 and
and 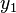 after the transformation are:
after the transformation are: