Adjugate Formula
| ← Back: Gauß-Jordan-Algorithm | Overview: Matrix inversion | Next: Transformations → |
The adjugate formula defines the inverse of an n-by-n square matrix 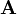 as
as
where 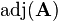 is the so called adjugate matrix of
is the so called adjugate matrix of 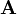 . The adjugate matrix is the transposed of the cofactor matrix:
. The adjugate matrix is the transposed of the cofactor matrix:
And the cofactor matrix 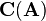 is just a matrix where each cell corresponds to the related cofactor:
is just a matrix where each cell corresponds to the related cofactor:
So to determine the inverse of an n-by-n square matrix you have to compute the n square cofactors, then transpose the resulting cofactor matrix and divide all the values by the determinant.
The following matrix is already used in examples for the minors and cofactors and for the determinant.
The computation of the cofactors is easy in this case because the minors correspond to the determinants of 1-by-1 matrices, that are the value itself. So the cofactor matrix of matrix The transposed of the cofactor matrix which corresponds to the adjugate matrix then appears as
The determinant is computed in the example for a determinant of a matrix and equals 1. So the inverse of For a proof please have a look at the example in the main article of matrix inversion. |
The following matrix is already used in examples for the minors and cofactors and for the determinant.
The calculation of two of the cofactors of The transposed of the cofactor matrix which corresponds to the adjugate matrix then appears as
The determinant is computed in the example for a determinant of a matrix and equals 1. So the inverse of For a proof please have a look at the example in the main article of matrix inversion. |
In this example again the transformation matrix The calculation of two of the cofactors of The transposed of the cofactor matrix which corresponds to the adjugate matrix then appears as
The determinant is computed in the example for a determinant of a matrix and equals 1. So the inverse of For a proof please have a look at the example in the main article of matrix inversion. |
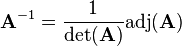
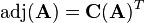
![\mathbf{C}(\mathbf{A})=\left[\begin{array}{cccc}
C_{11}(\mathbf{A}) & C_{12}(\mathbf{A}) & \cdots & C_{1n}(\mathbf{A})\\
C_{21}(\mathbf{A}) & C_{22}(\mathbf{A}) & & C_{2n}(\mathbf{A})\\
\vdots & & \ddots & \vdots\\
C_{n1}(\mathbf{A}) & C_{n2}(\mathbf{A}) & \cdots & C_{nn}(\mathbf{A})
\end{array}\right]](/wiki/robotics/images/math/8/4/d/84de09df69b63883c3544929bdfaad78.png)
![\mathbf{A}_2 =
\left[\begin{array}{cc}
2&3\\
1&2
\end{array}\right]](/wiki/robotics/images/math/4/6/d/46de04a2d87fbf4420b70503cd822eda.png)
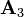 is
is![\mathbf{C}(\mathbf{A}_2)=
\left[\begin{array}{cc}
(-1)^{1+1}\det
\left[\begin{array}{cc}
\Box&\Box\\
\Box&2
\end{array}\right]
& (-1)^{1+2}\det
\left[\begin{array}{cc}
\Box&\Box\\
1&\Box
\end{array}\right]
\\ \\
(-1)^{2+1}\det
\left[\begin{array}{cc}
\Box&3\\
\Box&\Box
\end{array}\right]
& (-1)^{2+2}\det
\left[\begin{array}{cc}
2&\Box\\
\Box&\Box
\end{array}\right]
\end{array}\right]=
\left[\begin{array}{cc}
(-1)^{1+1}\det[2] & (-1)^{1+2}\det[1]\\
(-1)^{2+1}\det[3] & (-1)^{2+2}\det[2]
\end{array}\right]=
\left[\begin{array}{cc}
2 & -1\\
-3 & 2
\end{array}\right]](/wiki/robotics/images/math/d/2/9/d29792c826b9daad55e9007088d1cac6.png)
![\mathbf{C}(\mathbf{A}_2)^T=
\left[\begin{array}{cc}
2&-3\\
-1&2
\end{array}\right]=\text{adj}(\mathbf{A}_2)](/wiki/robotics/images/math/c/f/a/cfa55a5df9f2bdbd8978f7412622a207.png)
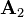 is determined as
is determined as ![\mathbf{A}_2^{-1}=\frac{1}{\det(\mathbf{A}_2)}\text{adj}(\mathbf{A}_2)
=\frac{1}{1}
\left[\begin{array}{cc}
2&-3\\
-1&2
\end{array}\right]
=
\left[\begin{array}{cc}
2&-3\\
-1&2
\end{array}\right]](/wiki/robotics/images/math/1/f/1/1f15d665f0eff70e24f298489e7f2dae.png)
![\mathbf{A}_3 =
\left[\begin{array}{ccc}
1&0&1\\
3&1&0\\
1&0&2
\end{array}\right]](/wiki/robotics/images/math/4/7/f/47ff3b29442735c862d2f12e20505fa0.png)
![\mathbf{C}(\mathbf{A}_3)=
\left[\begin{array}{ccc}
2&-6&-1\\
0&1&0\\
-1&3&1
\end{array}\right]](/wiki/robotics/images/math/4/1/3/413b005a3536c35401cbcfe6d548e642.png)
![\mathbf{C}(\mathbf{A}_3)^T=
\left[\begin{array}{ccc}
2&0&-1\\
-6&1&3\\
-1&0&1
\end{array}\right]=\text{adj}(\mathbf{A}_3)](/wiki/robotics/images/math/b/7/0/b70ce4db001e413432a52d84e08cbbbd.png)
![\mathbf{A}_3^{-1}=\frac{1}{\det(\mathbf{A}_3)}\text{adj}(\mathbf{A}_3)
=\frac{1}{1}
\left[\begin{array}{ccc}
2&0&-1\\
-6&1&3\\
-1&0&1
\end{array}\right]
=
\left[\begin{array}{ccc}
2&0&-1\\
-6&1&3\\
-1&0&1
\end{array}\right]](/wiki/robotics/images/math/9/6/2/962487deb0223be3581bf22e557eb63f.png)
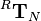 that is introduced in the robotics script in chapter 3 on page 3-37 is used:
that is introduced in the robotics script in chapter 3 on page 3-37 is used:
![^R\mathbf{T}_N =
\left[\begin{array}{cccc}
0 & 1 & 0 & 2a\\
0 & 0 & -1 & 0\\
-1 & 0 & 0 & 0\\
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/8/5/e/85e5abe5247392c6a2634922b8382d3d.png)
![\mathbf{C}(^R\mathbf{T}_N)=
\left[\begin{array}{cccc}
0&1&0&0\\
0&0&-1&0\\
-1&0&0&0\\
0&-2a&0&1
\end{array}\right]](/wiki/robotics/images/math/9/7/9/979818594aa41845e5c4d89b5cf04ba4.png)
![\mathbf{C}(^R\mathbf{T}_N)^T=
\left[\begin{array}{cccc}
0&0&-1&0\\
1&0&0&-2a\\
0&-1&0&0\\
0&0&0&1
\end{array}\right]=\text{adj}(^R\mathbf{T}_N)](/wiki/robotics/images/math/f/a/2/fa20d0dd2b586965eae12f5143e362b0.png)
![^R\mathbf{T}_N^{-1}=\frac{1}{\det(^R\mathbf{T}_N)}\text{adj}(^R\mathbf{T}_N)
=\frac{1}{1}
\left[\begin{array}{cccc}
0&0&-1&0\\
1&0&0&-2a\\
0&-1&0&0\\
0&0&0&1
\end{array}\right]
=
\left[\begin{array}{cccc}
0&0&-1&0\\
1&0&0&-2a\\
0&-1&0&0\\
0&0&0&1
\end{array}\right]](/wiki/robotics/images/math/f/b/1/fb1700297fa86ac28fa5f9f48c40690c.png)