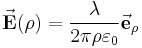Zylinderkoordinaten: Unterschied zwischen den Versionen
(Die Seite wurde geleert.) |
|||
| (36 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{Navigation|before=[[Das kartesische Koordinatensystem]]|overview=[[Orthogonale Koordinatensysteme:Übersicht|Orthogonale Koordinatensysteme]]|next=[[Kugelkoordinaten]]}} | ||
| + | [[Image:Zylinderkoordinaten.png|400px|thumb|<caption>Zylinderkoordinaten</caption>]] | ||
| + | Das Zylinderkoordinatensystem ermöglicht insbesondere dann eine kompakte Beschreibung von Positionen und gerichteten Größen im Raum, wenn man es mit zylinderförmigen Anordnungen zu tun hat. Das elektrische Feld einer Linienladung, die näherungsweise als zylinderförmig angenommen werden kann, lässt sich zum Beispiel wesentlich einfacher in Zylinder- als in [[kartesische Koordinaten|kartesischen Koordinaten]] beschreiben (vgl. Beispiel unten). Es gibt zahlreiche weitere Beispiele wie die Beschreibung des elektrischen Feldes einer zylinderförmigen Raumladung oder die Beschreibung des magnetischen Feldes eines stromdurchflossenen Leiters. Bei dem Zylinderkoordinatensystem handelt es sich um ein [[Krummlinige orthogonale Koordinatensysteme|krummliniges orthogonales Koordinatensystem]]. | ||
| + | |||
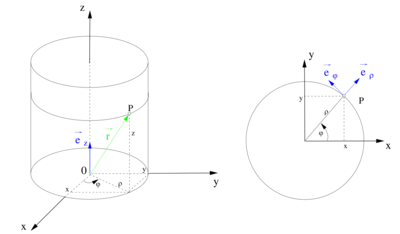
| + | Bei den Zylinderkoordinaten wird ein Punkt <math>P</math> im Raum durch die drei Koordinaten <math>\rho</math>, <math>\varphi</math> und <math>z</math> beschrieben. Dabei bleibt die <math>z</math>-Achse des kartesischen Koordinatensystems unverändert erhalten. <math>\rho</math> (je nach Quelle auch als <math>r</math> bezeichnet) gibt den Abstand zur <math>z</math>-Achse an und <math>\varphi</math> bezeichnet den Winkel zum betrachteten Punkt. Dabei wird <math>\varphi</math> ausgehend von der positiven <math>x</math>-Achse in Richtung der positiven <math>y</math>-Achse gezählt. Somit ist der positiven <math>x</math>-Achse der Winkel <math>\varphi=0</math> und der negativen <math>x</math>-Achse der Winkel <math>\varphi = \pi</math> zugeordnet. | ||
| + | |||
| + | Die Richtung der [[Einheitsvektoren]] <math>\vec{\textbf{e}}_\rho</math> und <math>\vec{\textbf{e}}_\varphi</math> hängt von der Position des betrachteten Punktes ab. Die nebenstehende Abbildung verdeutlicht, dass <math>\vec{\mathbf{e}}_\varphi</math> immer tangential zu dem Kreisbogen (<math>\varphi</math>-[[Koordinatenlinie]]) im Punkt <math>P</math> verläuft und <math>\vec{\mathbf{e}}_\rho</math> immer orthogonal auf diesem Kreisbogen steht. Der Einheitsvektor <math>\vec{\textbf{e}}_z</math> (vgl. [[kartesische Koordinaten]]) zeigt unabhängig vom betrachteten Punkt im Raum immer in dieselbe Richtung. | ||
| + | |||
| + | Betrachtet man ausschließlich die <math>x</math>-<math>y</math>-Ebene ohne die <math>z</math>-Achse, so handelt es sich um '''Polarkoordinaten'''. | ||
| + | |||
| + | Die Koordinaten und Einheitsvektoren der verschiedenen Koordinatensysteme können mit Hilfe von Transformationsgleichungen ineinander umgerechnet werden (siehe hierzu [[Formelsammlung Koordinatensysteme]]). Möchte man beispielsweise den Wert <math>x</math> in kartesischen Koordinaten eines in Zylinderkoordinaten gegebenen Punktes <math>P(\rho,\varphi,z)</math> ermitteln, so bietet sich die Verwendung [[Trigonometrische Funktionen|trigonometrischer Funktionen]] an. Aus der Abbildung wird ersichtlich, dass <math>\rho</math> der Hypotenuse und <math>x</math> der Ankathete in Bezug auf das durch <math>\varphi</math> gegebene rechtwinklige Dreieck entspricht. Damit gilt: | ||
| + | :<math> | ||
| + | \cos\varphi = \frac{x}{\rho}\,\Rightarrow\, x = \rho \cos\varphi | ||
| + | </math> | ||
| + | Für die <math>y</math>-Koordinate kann analog verfahren werden und die <math>z</math>-Koordinate bleibt erhalten. Umgekehrt lassen sich auch Zylinderkoordinaten aus gegebenen kartesischen Koordinaten berechnen, die entsprechenden Transformationsgleichungen sind in der folgenden Tabelle angegeben: | ||
| + | |||
| + | {|cellpadding="10" | ||
| + | |rowspan="3" style="background-color:#dde6f3;"|Umrechnung von Zylinder-<br> in kartesische Koordinaten | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | x &= \rho \cos \varphi& | ||
| + | &\text{mit}& | ||
| + | 0 &\leq \rho < \infty | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |rowspan="3" style="background-color:#dde6f3;"|Umrechnung von kartesischen-<br>in Zylinderkoordinaten | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \rho &=\sqrt{x^2+y^2} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | y &= \rho \sin \varphi& | ||
| + | &\text{mit}& | ||
| + | 0 &\leq \varphi < 2 \pi | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \varphi &=\arctan\frac{y}{x}\ \text{wenn}\ x>0 | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | z &= z& | ||
| + | && && && | ||
| + | &\text{mit}& | ||
| + | -\infty &\leq z\leq\infty | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | z &=z | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |||
| + | Aus der Abbildung wird außerdem ersichtlich, dass der [[Ortsvektor]] in Zylinderkoordinaten wie folgt beschrieben wird: | ||
| + | :<math> | ||
| + | \vec{\textbf{r}} = \rho\,\vec{\textbf{e}}_\rho + z\,\vec{\mathbf{e}}_\mathrm{z} | ||
| + | </math> | ||
| + | Eine differentielle ([[Infinitesimale Weg-, Flächen-, und Volumenelemente|infinitesimale]]) Änderung des Ortsvektors <math>\mathrm{d}\vec{\textbf{r}}</math> ausgehend vom Punkt <math>P</math> um <math>\mathrm{d}\rho, \mathrm{d}\varphi, \mathrm{d}z</math> wird wie folgt beschrieben: | ||
| + | :<math> | ||
| + | \mathrm{d}\vec{\textbf{r}} = | ||
| + | \vec{\textbf{e}}_\rho \mathrm{d}\rho + | ||
| + | \vec{\textbf{e}}_\varphi \rho \mathrm{d}\varphi + | ||
| + | \vec{\textbf{e}}_\mathrm{z} \mathrm{d}z | ||
| + | </math> | ||
| + | Für weitere Umrechnungen und Zusammenhänge wird auf die [[Formelsammlung Koordinatensysteme]] verwiesen. | ||
| + | |||
| + | Je nachdem, in welchen Bereichen (Intervallen) sich die Koordinaten bewegen, werden verschiedene [[Wegelemente|Linien-]], [[Fächenelemente|Flächen-]] und [[Volumenelemente]] beschrieben. Hält man z. B. alle Koordinaten bis auf <math>\varphi</math> konstant, so ergeben sich Kreise (vgl. [[Koordinatenlinien]]). Zur Verdeutlichung dieser Zusammenhänge kann das unten eingebundene Applet verwendet werden. | ||
| + | |||
| + | {{Beispiel | ||
| + | |Titel=Elektrisches Feld einer Linienladung | ||
| + | |Inhalt= | ||
| + | Das elektrische Feld einer Linienladung <math>\lambda</math> zeigt radialsymmetrisch in den Raum und ist nur vom Abstand <math>\rho</math> abhängig. | ||
| + | |||
| + | [[Datei:Linienladung_und_E-feld.svg|500px]] | ||
| + | |||
| + | |||
| + | Damit kann die elektrische Feldstärke <math>\vec{\textbf{E}}</math> besonders kompakt in Zylinderkoordinaten angegeben werden: | ||
| + | :<math> | ||
| + | \vec{\textbf{E}}(\rho) = \frac{\lambda}{2\pi\rho\varepsilon_0} \vec{\textbf{e}}_\rho | ||
| + | </math> | ||
| + | }} | ||
| + | |||
| + | ====Applet==== | ||
| + | [[Datei:Applet_Zylinderkoordinaten.png|200px|gerahmt|links|verweis=Applet:Zylinderkoordinaten|[[Applet:Zylinderkoordinaten|Applet Zylinderkoordinaten]]]] | ||
| + | |||
| + | <!-- alt | ||
| + | ---- | ||
| + | '''Alt''' | ||
| + | ---- | ||
| + | Betrachtet man das Modell eines Kabels, ist es häufig problematisch, Effekte mathematisch im gewohnten [[Das kartesische Koordinatensystem|kartesischen Koordinatensystem]] zu beschreiben. Durch die Wölbung der Oberfläche muss im kartesischen System immer ein sich verändernder Winkel mitbetrachtet werden, selbst wenn die Effekte, die man beschreiben will, senkrecht oder parallel zu dem Kabel verlaufen. Um sich die Rechnung zu vereinfachen, wählt man insbesondere für Probleme mit konzentrischen oder radialen Anordnungen einen Sonderfall der krummlinigen orthogonalen Koordinatensysteme, die '''Zylinderkoordinaten''': | ||
| + | |||
| + | <figure id="fig:krummlinige_koordinaten3"> | ||
| + | [[Image:Zylinderkoordinaten.png|400px|thumb|<caption>Zylinderkoordinaten</caption>]] | ||
| + | </figure> | ||
| + | |||
| + | Albachversion: | ||
| + | [[Image:Koordinatensysteme_Krummlinige_Koordinaten3.jpg|400px|thumb|<caption>Zylinderkoordinaten</caption>]] | ||
| + | |||
| + | Um die Zylinderkoordinaten zu verstehen, hilft es, sich einen Zylinder vorzustellen und ihn in seine Bestandteile, also Deckel und Mantelflächen zu unterteilen. Die Deckelfläche lässt sich dabei am einfachsten mit ihrem Radius <math>\rho</math> und dem Winkel <math>\varphi</math> beschreiben (siehe Abbildung). Eben diese Koordinaten werden bei den ebenen Zylinderkoordinaten (auch: '''Polarkoordinaten''') verwendet. Dabei wird der Winkel <math>\varphi</math> definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt. | ||
| + | Um die Höhe berücksichtigen zu können, wählt man die z-Koordinate, die schon aus den kartesischen Koordinaten bekannt ist. Diese entspricht der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen. | ||
| + | |||
| + | '''Aufgepasst''':Im Gegensatz zu den [[Einheitsvektoren]] der kartesischen Koordinaten verändern die Einheitsvektoren der Zylinderkoordinaten (<math>\vec{\mathbf{e}}_\rho</math> und <math>\vec{\mathbf{e}}_\varphi</math>) ihre Richtung mit wachsenden Koordinatenwerten. Aus der Abbildung wird klar, dass <math>\vec{\mathbf{e}}_\varphi</math> immer tangential zu dem Kreisbogen im Punkt ''P'' verläuft und <math>\vec{\mathbf{e}}_\rho</math> immer orthogonal auf dem Kreisbogen steht. | ||
| + | |||
| + | Um zwischen Koordinatensystemen wechseln zu können, braucht man die '''Transformationsgleichungen'''. Zur Berechnung verwendet man die [[Trigonometrischen Funktionen]]. Als Beispiel soll die Koordinate x durch die Zylinderkoordinaten dargestellt werden. Dazu benötigt man die Parameter <math>\rho</math> und <math>\varphi</math>, da die z-Koordinate in beiden Systemen äquivalent ist. Betrachtet man nun die Abbildung, erkennt man, dass <math>\rho</math> der Hypotenuse und x der Ankathete entspricht: | ||
| + | :<math>\frac{x}{\rho}=\cos(\varphi)</math> | ||
| + | Stellt man diese Gleichung nach x um, erhält man die erste Transformationsgleichung. Die zweite Transformationsgleichung ergibt sich aus der selben Überlegung, nur entspricht die y-Achse der Gegenkathete, daher erhält man den Sinus in der zweiten Gleichung: | ||
| + | |||
| + | {| cellpadding="10" | ||
| + | | rowspan="3" style="background-color:#dde6f3;" |Transformationsgleichung | ||
| + | | style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \mathrm{x} &= \rho \cos \varphi& | ||
| + | &\text{mit}& | ||
| + | 0 &\leq \rho < \infty | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \mathrm{y} &= \rho \sin \varphi& | ||
| + | &\text{mit}& | ||
| + | 0 &\leq \varphi < 2 \pi | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \mathrm{z} &= \mathrm{z}& | ||
| + | && && && | ||
| + | &\text{mit}& | ||
| + | -\infty &\leq z\leq\infty | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |||
| + | Möchte man aus dem Zylinderkoordinatensystem wieder in das kartesische Koordinatensystem zurücktransformieren, muss man die oberen Tranformationsgleichungen umstellen und man erhält entsprechend: | ||
| + | |||
| + | |||
| + | {| cellpadding="10" | ||
| + | | rowspan="3" style="background-color:#dde6f3;" |Transformationsgleichung | ||
| + | | style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \rho &=\sqrt{x^2+y^2} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \varphi &=\arctan{\frac{y}{x}} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | z &=z | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |||
| + | Nur die Transformationsgleichungen reichen nicht, um die kartesischen Koordinaten durch Zylinderkoordinaten auszudrücken, da die Einheitsvektoren nach wie vor kartesisch dargestellt werden. Um auch sie umzuwandeln, kann man folgende Form verwenden: | ||
| + | |||
| + | :<math> | ||
| + | \vec{\textbf{e}}_i = \frac{1}{\left|\frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i}\right|} \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i} = \frac{1}{h_i} \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i} | ||
| + | \text{mit}\ | ||
| + | h_i = \left| \frac{\partial \vec{\textbf{r}}}{\partial \mathrm{u}_i} \right| | ||
| + | </math> | ||
| + | |||
| + | Hier wird also der '''[[Ortsvektor]]''' (Ein Vektor, der vom Ursprung bis zu den Punkten im Raum verläuft. Die Berechnung des Ortsvektors wird im unteren Beispiel veranschaulicht. Hier genügt es zu wissen, dass der Ortsvektor in kartesischen Koordinaten folgende Funktion besitzt: <math>\vec{\textbf{r}} = \vec{\textbf{e}}_\mathrm{x}x +\vec{\textbf{e}}_\mathrm{y} y + \vec{\textbf{e}}_\mathrm{z} \mathrm{z}</math>) nach der jeweiligen Koordinate abgeleitet und durch den '''Metrikkoeffizienten''' <math>h_i</math> geteilt. | ||
| + | |||
| + | Anschaulich bedeutet das, dass die partielle Ableitung des Ortsvektors nach der jeweiligen Koordinate gesucht ist. Diese ist nichts weiter als die '''Änderungsgeschwindigkeit''' des Ortsvektors, also wie schnell sich dieser bei dem Verändern der Koordinate "bewegt" oder wie stark die Änderung des Einheitsvektors von Punkt zu Punkt ist. | ||
| + | Da Einheitsvektoren so definiert sind, dass sie immer die Länge 1 haben müssen, wird der Einheitsvektor noch normiert. Dazu verwendet man den Metrikkoeffizienten, da dieser den Betrag der Änderung des Ortsvektors bestimmt. Übrig bleibt ein Vektor in Richtung der Änderung mit dem Betrag eins. | ||
| + | Zur Veranschalichung der Rechnung wird sie hier anhand eines Beispiels der Koordinate <math>\varphi</math> aufgeschlüsselt. | ||
| + | |||
| + | Zunächst wird der Metrikkoeffizient berechnet, dazu müssen für die Variablen x,y,z die Transformationsgleichungen eingesetzt und nach der Koordinate <math>\varphi</math> differenziert werden. Anschließend wird der Betrag gebildet: | ||
| + | |||
| + | :<math> | ||
| + | \begin{align} | ||
| + | h_\varphi & = | ||
| + | \sqrt{ | ||
| + | \left( \frac{\partial \mathrm{x}}{\partial \mathrm{\varphi}} \right)^2 + | ||
| + | \left( \frac{\partial \mathrm{y}}{\partial \mathrm{\varphi}} \right)^2 + | ||
| + | \left( \frac{\partial \mathrm{z}}{\partial \mathrm{\varphi}} \right)^2}\\ | ||
| + | & =\sqrt{ | ||
| + | \left( \frac{\partial \mathrm{\rho \cos \varphi}}{\partial \mathrm{\varphi}} \right)^2 + | ||
| + | \left( \frac{\partial \mathrm{\rho \sin \varphi}}{\partial \mathrm{\varphi}} \right)^2 + | ||
| + | \left( \frac{\partial \mathrm{z}}{\partial \mathrm{\varphi}} \right)^2}\\ | ||
| + | & =\sqrt{(-\rho\sin\varphi)^2+(\rho\cos\varphi)^2} | ||
| + | =(\rho^2\underbrace {(sin^2\varphi+\cos^2\varphi)}_{1})^{\frac{1}{2}}=\rho | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Die beiden anderen metrischen Koeffizienten ergeben sich zu: | ||
| + | :<math> h_\rho = h_\mathrm{z} = 1</math> | ||
| + | |||
| + | Hat man nun die Metrikkoeffizienten oder metrischen Faktoren, kann man die Einheitsvektoren des Zylinderkoordinatensystems bestimmen. Dazu leitet man wie schon bei dem Metrikkoeffizienten den Ortsvektor nach der gesuchten Koordinate ab und man erhält: | ||
| + | |||
| + | {| cellpadding="10" | ||
| + | | rowspan="3" style="background-color:#dde6f3;" |Einheitsvektoren | ||
| + | | style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \vec{\textbf{e}}_1 &= \vec{\textbf{e}}_\rho = \frac{\partial \vec{\textbf{r}}}{\partial \rho} = | ||
| + | \vec{\textbf{e}}_\mathrm{x} \cos \varphi + \vec{\textbf{e}}_\mathrm{y} \sin \varphi | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \vec{\textbf{e}}_2 &= \vec{\textbf{e}}_\varphi = \frac{\partial \vec{\textbf{r}}}{\rho \partial \varphi} = -\vec{\textbf{e}}_\mathrm{x} \sin \varphi + \vec{\textbf{e}}_\mathrm{y} \cos \varphi | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | \vec{\textbf{e}}_3 &= \vec{\textbf{e}}_\mathrm{z} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |||
| + | Zwei weitere wichtige Parameter im Zylinderkoordinatensystem sind das '''vektorielle Wegelement''': | ||
| + | :<math> | ||
| + | \mathrm{d}\vec{\textbf{r}} = | ||
| + | \vec{\textbf{e}}_\rho \mathrm{d}\rho + | ||
| + | \vec{\textbf{e}}_\varphi \rho \mathrm{d}\varphi + | ||
| + | \vec{\textbf{e}}_\mathrm{z} \mathrm{d}\mathrm{z} | ||
| + | </math> | ||
| + | und das '''Volumenelement''': | ||
| + | :<math> | ||
| + | \mathrm{d}V = \rho\mathrm{d}\rho \mathrm{d}\varphi \mathrm{d}\mathrm{z} | ||
| + | </math> | ||
| + | |||
| + | {{Beispiel | ||
| + | |Titel=Beschreibung des Ortsvektors in Zylinderkoordinaten | ||
| + | |Inhalt= | ||
| + | [[Image:Zylinderkoordinaten.png|center|300px]] | ||
| + | |||
| + | Albachversion: | ||
| + | [[Image:Koordinatensysteme_Krummlinige_Koordinaten3.jpg|400px|thumb|<caption>Zylinderkoordinaten</caption>]] | ||
| + | |||
| + | Warum es sich lohnt eine Koordinatentransformation durchzuführen, soll anhand dieses Beispiels verdeutlicht werden. Hier soll der Ortsvektor, eine Funktion, bei der der Vektor vom Koordinatenursprung auf einen Punkt abgebildet wird, in zylindrischen Koordinaten ausgedrückt werden, da diese Darstellung in Zylinderkoordinaten viel übersichtlicher ist, als die Darstellung in den kartesischen Koordinaten. Dafür sei der Ortsvektor <math>\vec{\mathbf{r}}</math> in kartesischen Koordinaten gegeben: | ||
| + | :<math>\vec{\mathbf{r}}=\vec{\mathbf{e}}x\cdot x+\vec{\mathbf{e}}y\cdot y+\vec{\mathbf{e}}z\cdot z</math> | ||
| + | |||
| + | Als erstes drückt man diesen Vektor in zylindrischen Koordinaten mithilfe der Transformationsgleichungen aus und fasst die ersten beiden Terme zusammen: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | \vec{\textbf{r}} & = \vec{\textbf{e}}_\mathrm{x} \rho \cos \varphi + \vec{\textbf{e}}_\mathrm{y} \rho \sin \varphi + \vec{\textbf{e}}_\mathrm{z} \mathrm{z}\\ | ||
| + | & = \rho (\vec{\textbf{e}}_\mathrm{x} \cos \varphi + \vec{\textbf{e}}_\mathrm{y} \sin \varphi) + \vec{\textbf{e}}_\mathrm{z} \mathrm{z} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Vergleicht man die Beziehungen mit den Einheitsvektoren des Zylinderkoordinatensystems, sieht man sofort, dass die kartesischen Einheitsvektoren <math>\vec{\textbf{e}}_x</math> und <math>\vec{\textbf{e}}_y</math> sich im zylindrischen System in dem Einheitsvektor <math>\vec{\textbf{e}}_\rho</math> ausdrücken lassen: | ||
| + | |||
| + | :<math> | ||
| + | \begin{align} | ||
| + | \vec{\textbf{e}}_\rho & = \frac{\partial \vec{\textbf{r}}}{\partial \rho} = | ||
| + | \vec{\textbf{e}}_\mathrm{x} \cos \varphi + \vec{\textbf{e}}_\mathrm{y} \sin \varphi\\ | ||
| + | \vec{\textbf{e}}_3 &= \vec{\textbf{e}}_\mathrm{z} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | Durch einsetzen des Einheitsvektors <math>\vec{\textbf{e}}_\rho</math> erhält man die folgende, viel einfachere Darstellung des Ortsvektors in Zylinderkoordinaten: | ||
| + | :<math> | ||
| + | \vec{\textbf{r}} = \vec{\textbf{e}}_\rho \rho + \vec{\mathbf{e}}_\mathrm{z} \mathrm{z} | ||
| + | </math> | ||
| + | }} | ||
| + | --> | ||
| + | <div style="clear:left;"> | ||
| + | </div> | ||
| + | {{Multimedia|Links= | ||
| + | http://demonstrations.wolfram.com/ExploringCylindricalCoordinates/ '''Applet''': Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) | ||
| + | |||
| + | http://demonstrations.wolfram.com/CylindricalCoordinates/ '''Applet''': Punkt in Zylinderkoordinaten | ||
| + | (engl./ free CDF-Player erforderlich) | ||
| + | }} | ||
| + | |||
| + | {{Link|Links= | ||
| + | http://www.math.wpi.edu/Course_Materials/MA2251C99/images/cylndrcl.gif Bild zu infinitesimalen Volumenelement in Zylinderkoordinatensystem | ||
| + | |||
| + | http://lh5.ggpht.com/_XvrTyMj5b-k/SaH0PTc-qWI/AAAAAAAAFnM/YYo0W-gT_5I/controlvolumecylindricalcontinuity5.png Bild zu einem infinitesimalen Volumenelement in Zylinderkoordinaten | ||
| + | |||
| + | http://scientificsentence.net/Electromagnetics/index.php?key=yes&Integer=Cylindrical Bild und Erläuterung zu den Einheitsvektoren im Zylinderkoordinatensystem (engl.) | ||
| + | }} | ||
| + | |||
| + | <noinclude>==Literatur== | ||
| + | * Manfred Albach, ''Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen'', 3. Auflage (Pearson Studium, 2011) | ||
| + | </noinclude> | ||
| + | |||
| + | [[Kategorie:Artikel]] | ||
| + | [[Kategorie:Feedback]] | ||
Aktuelle Version vom 9. November 2017, 16:58 Uhr
| ← Zurück: Das kartesische Koordinatensystem | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Kugelkoordinaten → |
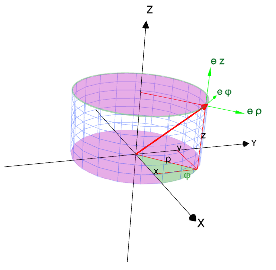
Das Zylinderkoordinatensystem ermöglicht insbesondere dann eine kompakte Beschreibung von Positionen und gerichteten Größen im Raum, wenn man es mit zylinderförmigen Anordnungen zu tun hat. Das elektrische Feld einer Linienladung, die näherungsweise als zylinderförmig angenommen werden kann, lässt sich zum Beispiel wesentlich einfacher in Zylinder- als in kartesischen Koordinaten beschreiben (vgl. Beispiel unten). Es gibt zahlreiche weitere Beispiele wie die Beschreibung des elektrischen Feldes einer zylinderförmigen Raumladung oder die Beschreibung des magnetischen Feldes eines stromdurchflossenen Leiters. Bei dem Zylinderkoordinatensystem handelt es sich um ein krummliniges orthogonales Koordinatensystem.
Bei den Zylinderkoordinaten wird ein Punkt 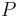 im Raum durch die drei Koordinaten
im Raum durch die drei Koordinaten 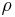 ,
,  und
und 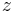 beschrieben. Dabei bleibt die
beschrieben. Dabei bleibt die 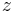 -Achse des kartesischen Koordinatensystems unverändert erhalten.
-Achse des kartesischen Koordinatensystems unverändert erhalten. 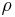 (je nach Quelle auch als
(je nach Quelle auch als 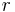 bezeichnet) gibt den Abstand zur
bezeichnet) gibt den Abstand zur 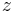 -Achse an und
-Achse an und  bezeichnet den Winkel zum betrachteten Punkt. Dabei wird
bezeichnet den Winkel zum betrachteten Punkt. Dabei wird  ausgehend von der positiven
ausgehend von der positiven  -Achse in Richtung der positiven
-Achse in Richtung der positiven 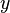 -Achse gezählt. Somit ist der positiven
-Achse gezählt. Somit ist der positiven  -Achse der Winkel
-Achse der Winkel 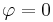 und der negativen
und der negativen  -Achse der Winkel
-Achse der Winkel 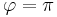 zugeordnet.
zugeordnet.
Die Richtung der Einheitsvektoren 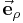 und
und 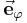 hängt von der Position des betrachteten Punktes ab. Die nebenstehende Abbildung verdeutlicht, dass
hängt von der Position des betrachteten Punktes ab. Die nebenstehende Abbildung verdeutlicht, dass 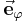 immer tangential zu dem Kreisbogen (
immer tangential zu dem Kreisbogen ( -Koordinatenlinie) im Punkt
-Koordinatenlinie) im Punkt 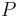 verläuft und
verläuft und 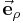 immer orthogonal auf diesem Kreisbogen steht. Der Einheitsvektor
immer orthogonal auf diesem Kreisbogen steht. Der Einheitsvektor 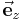 (vgl. kartesische Koordinaten) zeigt unabhängig vom betrachteten Punkt im Raum immer in dieselbe Richtung.
(vgl. kartesische Koordinaten) zeigt unabhängig vom betrachteten Punkt im Raum immer in dieselbe Richtung.
Betrachtet man ausschließlich die  -
-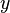 -Ebene ohne die
-Ebene ohne die 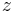 -Achse, so handelt es sich um Polarkoordinaten.
-Achse, so handelt es sich um Polarkoordinaten.
Die Koordinaten und Einheitsvektoren der verschiedenen Koordinatensysteme können mit Hilfe von Transformationsgleichungen ineinander umgerechnet werden (siehe hierzu Formelsammlung Koordinatensysteme). Möchte man beispielsweise den Wert  in kartesischen Koordinaten eines in Zylinderkoordinaten gegebenen Punktes
in kartesischen Koordinaten eines in Zylinderkoordinaten gegebenen Punktes 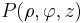 ermitteln, so bietet sich die Verwendung trigonometrischer Funktionen an. Aus der Abbildung wird ersichtlich, dass
ermitteln, so bietet sich die Verwendung trigonometrischer Funktionen an. Aus der Abbildung wird ersichtlich, dass 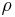 der Hypotenuse und
der Hypotenuse und  der Ankathete in Bezug auf das durch
der Ankathete in Bezug auf das durch  gegebene rechtwinklige Dreieck entspricht. Damit gilt:
gegebene rechtwinklige Dreieck entspricht. Damit gilt:
Für die 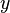 -Koordinate kann analog verfahren werden und die
-Koordinate kann analog verfahren werden und die 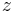 -Koordinate bleibt erhalten. Umgekehrt lassen sich auch Zylinderkoordinaten aus gegebenen kartesischen Koordinaten berechnen, die entsprechenden Transformationsgleichungen sind in der folgenden Tabelle angegeben:
-Koordinate bleibt erhalten. Umgekehrt lassen sich auch Zylinderkoordinaten aus gegebenen kartesischen Koordinaten berechnen, die entsprechenden Transformationsgleichungen sind in der folgenden Tabelle angegeben:
| Umrechnung von Zylinder- in kartesische Koordinaten |
|
Umrechnung von kartesischen- in Zylinderkoordinaten |
|
|
|
| ||
|
|
|
Aus der Abbildung wird außerdem ersichtlich, dass der Ortsvektor in Zylinderkoordinaten wie folgt beschrieben wird:
Eine differentielle (infinitesimale) Änderung des Ortsvektors 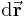 ausgehend vom Punkt
ausgehend vom Punkt 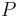 um
um 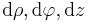 wird wie folgt beschrieben:
wird wie folgt beschrieben:
Für weitere Umrechnungen und Zusammenhänge wird auf die Formelsammlung Koordinatensysteme verwiesen.
Je nachdem, in welchen Bereichen (Intervallen) sich die Koordinaten bewegen, werden verschiedene Linien-, Flächen- und Volumenelemente beschrieben. Hält man z. B. alle Koordinaten bis auf  konstant, so ergeben sich Kreise (vgl. Koordinatenlinien). Zur Verdeutlichung dieser Zusammenhänge kann das unten eingebundene Applet verwendet werden.
konstant, so ergeben sich Kreise (vgl. Koordinatenlinien). Zur Verdeutlichung dieser Zusammenhänge kann das unten eingebundene Applet verwendet werden.
Das elektrische Feld einer Linienladung
|
Applet
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/ExploringCylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://demonstrations.wolfram.com/CylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) |
Hilfreiche Links
|
http://www.math.wpi.edu/Course_Materials/MA2251C99/images/cylndrcl.gif Bild zu infinitesimalen Volumenelement in Zylinderkoordinatensystem http://lh5.ggpht.com/_XvrTyMj5b-k/SaH0PTc-qWI/AAAAAAAAFnM/YYo0W-gT_5I/controlvolumecylindricalcontinuity5.png Bild zu einem infinitesimalen Volumenelement in Zylinderkoordinaten http://scientificsentence.net/Electromagnetics/index.php?key=yes&Integer=Cylindrical Bild und Erläuterung zu den Einheitsvektoren im Zylinderkoordinatensystem (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
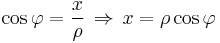
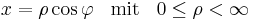
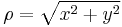
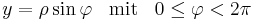
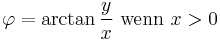
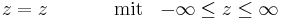

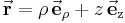
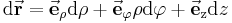
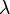 zeigt radialsymmetrisch in den Raum und ist nur vom Abstand
zeigt radialsymmetrisch in den Raum und ist nur vom Abstand 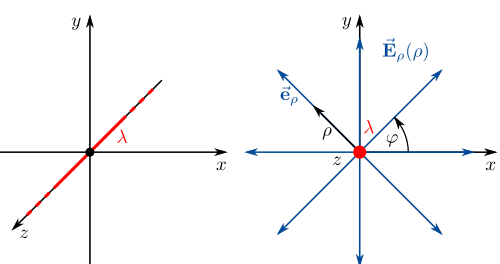
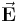 besonders kompakt in Zylinderkoordinaten angegeben werden:
besonders kompakt in Zylinderkoordinaten angegeben werden: