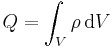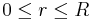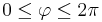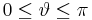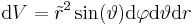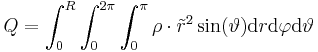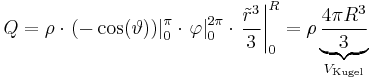Volumenelemente: Unterschied zwischen den Versionen
| Zeile 20: | Zeile 20: | ||
[[Datei:Volumenelement_Kugel.svg|600px|Volumenelement einer Kugel]] | [[Datei:Volumenelement_Kugel.svg|600px|Volumenelement einer Kugel]] | ||
| − | |||
Eine Übersicht dieser und weiterer Elemente in verschiedenen Koordinatensystemen findet sich in der [[Formelsammlung Koordinatensysteme]]. | Eine Übersicht dieser und weiterer Elemente in verschiedenen Koordinatensystemen findet sich in der [[Formelsammlung Koordinatensysteme]]. | ||
| Zeile 68: | Zeile 67: | ||
|Inhalt= | |Inhalt= | ||
[[Datei:Raumladung_einer_Kugel.svg|250px|thumb|right|Raumladung einer Kugel]] | [[Datei:Raumladung_einer_Kugel.svg|250px|thumb|right|Raumladung einer Kugel]] | ||
| − | Im zweiten Beispiel wird eine eine kugelförmige | + | Im zweiten Beispiel wird eine eine kugelförmige und konstante Raumladungsdichte <math>\rho</math> mit dem Radius <math>R</math> betrachtet. Um in diesem Fall die Gesamtladung <math>Q</math> bestimmen zu können, muss über das Volumen der Kugel integriert werden. In diesem Fall bietet sich aufgrund der Symmetrie die Berechnung in [[Kugelkoordinaten]] an: |
| − | + | :<math> | |
| − | :<math>Q=\int_V\rho\mathrm{d}V</math> | + | Q=\int_V\rho\,\mathrm{d}V |
| − | Um über | + | </math> |
| + | Um über das gesamte Kugelvolumen zu integrieren, müssen die Integrationsgrenzen wie folgt gewählt werden (vgl. [[Kugelkoordinaten]]). | ||
| + | :<math>0\leq r \leq R</math> | ||
:<math>0\leq\varphi\leq 2\pi</math> | :<math>0\leq\varphi\leq 2\pi</math> | ||
:<math>0\leq\vartheta\leq\pi</math> | :<math>0\leq\vartheta\leq\pi</math> | ||
| − | Außerdem muss das | + | Außerdem muss das Differntial in Kugelkoordinaten angegeben werden: |
| + | :<math> | ||
| + | \mathrm{d}V=\tilde r^2\sin(\vartheta)\mathrm{d}\varphi\mathrm{d}\vartheta\mathrm{d}r | ||
| + | </math> | ||
| − | :<math>\ | + | Durch Einsetzen folgt: |
| + | :<math> | ||
| + | Q=\int_0^R\int_0^{2\pi}\int_0^\pi\rho\cdot \tilde r^2\sin(\vartheta)\mathrm{d}r\mathrm{d}\varphi\mathrm{d}\vartheta | ||
| + | </math> | ||
| − | + | Da es sich bei <math>\rho</math> um eine konstante handelt, kann man diese Größe vor das Integral geschrieben werden und es folgt: | |
| − | + | :<math> | |
| − | + | Q=\rho\cdot \left.(-\cos(\vartheta))\right|_0^\pi\cdot\left.\varphi\right|_0^{2\pi}\cdot\left.\frac{\tilde r^3}{3}\right|_0^R=\rho\underbrace{\frac{4\pi R^3}{3}}_{V_{\text{Kugel}}} | |
| − | + | </math> | |
| − | Da <math>\rho</math> | + | Somit wird die Raumladungsdichte einfach mit dem Volumen einer Kugel mit dem Radius <math>R</math> multipliziert. Weitere Hinweise zur Lösung solcher Integrale finden sich im Artikel zur [[Lösung vektorieller Mehrfachintegrale|Lösung von Mehrfachintegralen]]. |
| − | |||
| − | :<math>Q=\rho\cdot \left.(-\cos(\vartheta))\right|_0^\pi\cdot\left.\varphi\right|_0^{2\pi}\cdot\left.\frac{\tilde r^3}{3}\right|_0^R=\rho\frac{4\pi R^3}{3}</math> | ||
| − | |||
| − | |||
}} | }} | ||
Version vom 29. August 2012, 22:51 Uhr
Infinitesimale Volumenelemente sind beliebig kleine Teilelemente eines Volumens, das meist mit 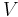 bezeichnet wird. Volumenelemente werden zum Beispiel im Zusammenhang mit Volumenintegralen benötigt. Prinzipiell handelt es sich um eine konsequente Fortsetzung der Beschreibung infinitesimaler Weg- und Flächenelemente. Infinitesimale Volumenelemente werden meist mit
bezeichnet wird. Volumenelemente werden zum Beispiel im Zusammenhang mit Volumenintegralen benötigt. Prinzipiell handelt es sich um eine konsequente Fortsetzung der Beschreibung infinitesimaler Weg- und Flächenelemente. Infinitesimale Volumenelemente werden meist mit 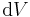 bezeichnet.
bezeichnet.
Da einem Volumen keine Richtung zugeordnet werden kann, tritt dieses Element immer nur als Betrag auf.
Ein infinitesimales Volumenelement ergibt sich gemäß der bekannten Regel „Grundfläche multipliziert mit der Höhe“, wobei die Grundfläche nun ein infinitesimales Flächenelement und die Höhe ein infinitesimales Wegelement darstellt. Somit ergibt sich ein infinitesimales Volumenelement in kartesischen Koordinaten wie folgt:
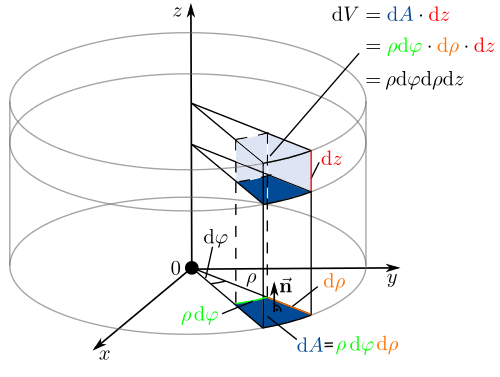
In der nachfolgenden Abbildung wird die Bestimmung eines infinitesimalen Volumenelements in Zylinderkoordinaten verdeutlicht:
Im Artikel Flächenelemente wurde bereits die Bestimmung einer infinitesimalen Kreisringfläche beschrieben. Die Fläche muss nun noch mit dem infinitesimalen Wegstück 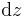 (entspricht der „Höhe“) multipliziert werden, so dass hier folgt:
(entspricht der „Höhe“) multipliziert werden, so dass hier folgt:
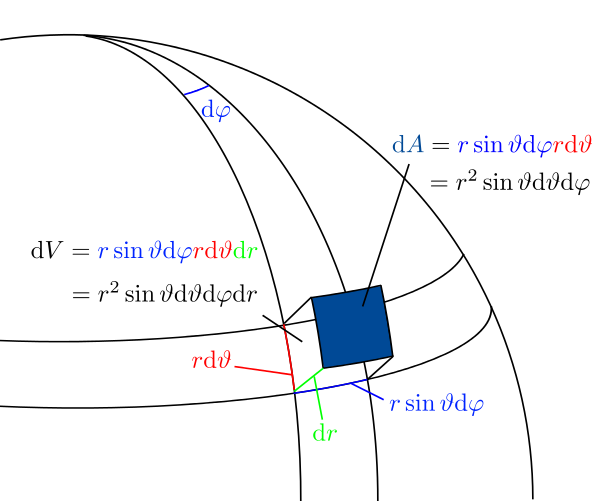
Ein Volumenelement in Kugelkoordinaten ergibt sich durch eine analoge Vorgehensweise, wobei hier nun mehrere gekrümmte Konturelemente zu berücksichtigen sind. Die nachfolgende Grafik verdeutlicht die Vorgehensweise:
Eine Übersicht dieser und weiterer Elemente in verschiedenen Koordinatensystemen findet sich in der Formelsammlung Koordinatensysteme.
In diesem Beispiel ist eine konstante Raumladungsdichte Ein Volumenelement in kartesischen Koordinaten wird wie folgt beschrieben: Es kann direkt in die Gleichung eingesetzt und das Integral gelöst werden. Da die Raumladungsdichte Damit folgt für die Gesamtladung: |
Im zweiten Beispiel wird eine eine kugelförmige und konstante Raumladungsdichte Um über das gesamte Kugelvolumen zu integrieren, müssen die Integrationsgrenzen wie folgt gewählt werden (vgl. Kugelkoordinaten). Außerdem muss das Differntial in Kugelkoordinaten angegeben werden: Durch Einsetzen folgt: Da es sich bei Somit wird die Raumladungsdichte einfach mit dem Volumen einer Kugel mit dem Radius |
Multimediale Lehrmaterialien
|
http://highered.mcgraw-hill.com/sites/0073451342/student_view0/chapter13/section6/cylindrical_coordinates__app_.html Darstellung von infinitesimalen Volumenelementen in Zylinderkoordinaten (engl.) |
Hilfreiche Links
|
http://web.mit.edu/8.02t/www/materials/modules/ReviewB.pdf Bebilderte Erklärung zu Kartesischen-, Kugel-, und Zylinderkoordinatensystemen und deren infinitesimalen Elementen (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Klaus Jänich Mathematik 1 Geschrieben für Physiker,2. Auflage (Springer Berlin Heidelberg, 2005)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Hempel, "Mathematische Grundlagen", Linienintegral, Universität Magdeburg
| ← Zurück: Flächenelemente | Übersicht: Infinitesimale Weg-, Flächen-, und Volumenelemente | Vorwärts: Infinitesimale Weg-, Flächen-, und Volumenelemente → |
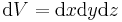
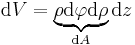
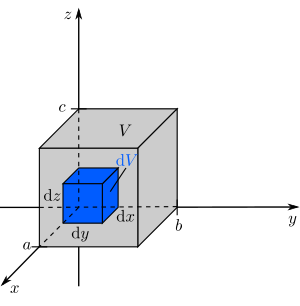
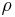 in einem Quader mit den Kantenlängen
in einem Quader mit den Kantenlängen 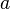 ,
, 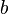 und
und 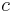 gegeben. Die Raumladungsdichte beschreibt die Ladungsmenge pro Volumen. Daher muss, um die Gesamtladung
gegeben. Die Raumladungsdichte beschreibt die Ladungsmenge pro Volumen. Daher muss, um die Gesamtladung 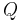 zu bestimmen, über das Volumen des Quaders integriert werden:
zu bestimmen, über das Volumen des Quaders integriert werden:
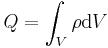
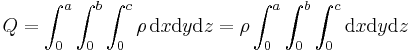
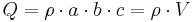
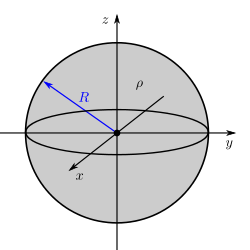
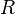 betrachtet. Um in diesem Fall die Gesamtladung
betrachtet. Um in diesem Fall die Gesamtladung