Difference between revisions of "Transformations"
| Line 36: | Line 36: | ||
This also holds for two, four and more dimensions. | This also holds for two, four and more dimensions. | ||
| − | By modifying the components of the transformation matrix different types of transformations can be achieved. In n-dimensional space rotation, scaling and shearing can basically be described by an n-by-n transformation matrix. Translation however is actually a [[ | + | By modifying the components of the transformation matrix different types of transformations can be achieved. In n-dimensional space rotation, scaling and shearing can basically be described by an n-by-n transformation matrix. Translation however is actually a [[Simple arithmetic operations|vector addition]] of an n-by-1 vector. These different in the following subarticles: |
# [[Translation]] | # [[Translation]] | ||
Revision as of 15:09, 26 May 2014
| ← Back: Adjugate Formula | Overview: Transformations | Next: Translation → |
In this article general transformations used in the context of robotics and the underlying mathematics are described.
Transformations are applied to vectors or coordinates in vector notation, respectively. All types of transformations can be achieved by matrix multiplication. To transform a vector 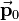 to
to 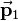 ,
, 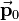 has to be multilplied by the transformation matrix
has to be multilplied by the transformation matrix 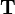 :
:
The basic transformation matrix is an identity matrix, which corresponds to an empty transformation. So an identity matrix as transformation matrix results in the original vector no matter how many dimensions the vector has. The following equation shows this for three dimensions:
This also holds for two, four and more dimensions.
By modifying the components of the transformation matrix different types of transformations can be achieved. In n-dimensional space rotation, scaling and shearing can basically be described by an n-by-n transformation matrix. Translation however is actually a vector addition of an n-by-1 vector. These different in the following subarticles:
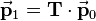
![\vec{\mathbf{p}}_1=\mathbf{I}_3\cdot\vec{\mathbf{p}}_0=
\left[\begin{array}{ccc}
1&0&0\\
0&1&0\\
0&0&1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0\\
y_0\\
z_0
\end{array}\right]=
\left[\begin{array}{c}
1\cdot x_0+0\cdot y_0+0\cdot z_0\\
0\cdot y_0+1\cdot y_0+0\cdot z_0\\
0\cdot y_0+0\cdot y_0+1\cdot z_0
\end{array}\right]=
\left[\begin{array}{c}
x_0\\
y_0\\
z_0
\end{array}\right]=
\vec{\mathbf{p}}_0](/wiki/robotics/images/math/0/4/0/040ad40d28470082eec49678f929423f.png)