Scaling

← Back: Translation

Overview: Transformations

Next: Rotation →

Scaling shifts coordinates similar to translation. The difference is, that translation is independent of the current coordinates. Scaling however shifts the coordinates depending on the current values. So the same transformation matrix has various effects on different vectors.

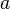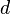For the sake of simplicity scaling is explained in two-dimensional space. But the behavior of the parameters is the same for an additional third dimension. Scaling is achieved by modifying the components $a$ and $d$ on the first diagonal of the transformation matrix 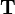$\mathbf{T}$, while the other components are zero:

$\mathbf{T}_s= \left[\begin{array}{cc} a & 0\\ 0 & d \end{array}\right]$

The computation of scaling looks as follows in coordinate notation:

$\vec{\mathbf{q}}_1=\mathbf{T}_s\cdot\vec{\mathbf{q}}_0= \left[\begin{array}{cc} a & 0\\ 0 & d \end{array}\right]\cdot \left[\begin{array}{c} x_0\\ y_0 \end{array}\right]= \left[\begin{array}{c} a\cdot x_0\\ d\cdot y_0 \end{array}\right]$

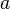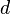So the values $a$ and $d$ act as factors for the x- and the y-component of the scaled vector.

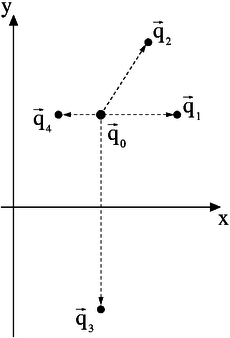
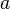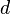Several different cases for $a$ and $d$ can be considered. The following transformation matrices show some of the possible cases, that achieve different scaling results (see figure):

$\mathbf{T}_0= \left[\begin{array}{cc} a=1 & 0\\ 0 & d=1 \end{array}\right]$

$\vec{\mathbf{q}}_0=\left[\begin{array}{c}x_1=x_0\\y_1=y_0\end{array}\right]$

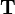$\mathbf{T}$ is the identity matrix → no effect

$\mathbf{T}_1= \left[\begin{array}{cc} a>1 & 0\\ 0 & d=1 \end{array}\right]$

$\vec{\mathbf{q}}_1=\left[\begin{array}{c}x_1>x_0\\y_1=y_0\end{array}\right]$

x-component is scaled up → vector is shifted to positive x-direction

$\mathbf{T}_2= \left[\begin{array}{cc} a>1 & 0\\ 0 & d>1 \end{array}\right]$

$\vec{\mathbf{q}}_2=\left[\begin{array}{c}x_2>x_0\\y_2>y_0\end{array}\right]$

x- and y-component are scaled up → vector is shifted diagonally to positive x- and y-direction

$\mathbf{T}_3= \left[\begin{array}{cc} a=1 & 0\\ 0 & d=-1 \end{array}\right]$

$\vec{\mathbf{q}}_3=\left[\begin{array}{c}x_3=x_0\\y_3=-y_0\end{array}\right]$

y-component is inverted → vector is reflected on x-axis to negative y-direction

$\mathbf{T}_4= \left[\begin{array}{cc} 0<a<1 & 0\\ 0 & d=1 \end{array}\right]$

$\vec{\mathbf{q}}_4=\left[\begin{array}{c}0<x_4<x_0\\y_4=y_0\end{array}\right]$

x-component is scaled down → vector is shifted closer to y-axis

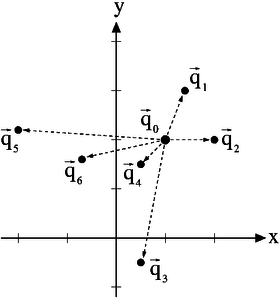
Example: Various scaling examples $\vec{\mathbf{q}}_0=\left[\begin{array}{c}1\\2\end{array}\right]$ $\mathbf{T}_1= \left[\begin{array}{cc} 1.4 & 0\\ 0 & 1.5 \end{array}\right]$ $\vec{\mathbf{q}}_1=\mathbf{T}_1\cdot \vec{\mathbf{q}}_0= \left[\begin{array}{cc} 1.4 & 0\\ 0 & 3 \end{array}\right] \cdot \left[\begin{array}{c}1\\2\end{array}\right]= \left[\begin{array}{c}1.4\\3\end{array}\right]$ $\mathbf{T}_2= \left[\begin{array}{cc} 2 & 0\\ 0 & 1 \end{array}\right]$ $\vec{\mathbf{q}}_2=\mathbf{T}_2\cdot \vec{\mathbf{q}}_0= \left[\begin{array}{cc} 2 & 0\\ 0 & 1 \end{array}\right] \cdot \left[\begin{array}{c}1\\2\end{array}\right]= \left[\begin{array}{c}2\\2\end{array}\right]$ $\mathbf{T}_3= \left[\begin{array}{cc} 0.5 & 0\\ 0 & -0.25 \end{array}\right]$ $\vec{\mathbf{q}}_3=\mathbf{T}_3\cdot \vec{\mathbf{q}}_0= \left[\begin{array}{cc} 0.5 & 0\\ 0 & -0.25 \end{array}\right] \cdot \left[\begin{array}{c}1\\2\end{array}\right]= \left[\begin{array}{c}0.5\\-0.5\end{array}\right]$ $\mathbf{T}_4= \left[\begin{array}{cc} 0.5 & 0\\ 0 & 0.75 \end{array}\right]$ $\vec{\mathbf{q}}_4=\mathbf{T}_4\cdot \vec{\mathbf{q}}_0= \left[\begin{array}{cc} 0.5 & 0\\ 0 & 0.75 \end{array}\right] \cdot \left[\begin{array}{c}1\\2\end{array}\right]= \left[\begin{array}{c}0.5\\1.5\end{array}\right]$ $\mathbf{T}_5= \left[\begin{array}{cc} -2 & 0\\ 0 & 1.1 \end{array}\right]$ $\vec{\mathbf{q}}_5=\mathbf{T}_5\cdot \vec{\mathbf{q}}_0= \left[\begin{array}{cc} -2 & 0\\ 0 & 1.1 \end{array}\right] \cdot \left[\begin{array}{c}1\\2\end{array}\right]= \left[\begin{array}{c}-2\\2.2\end{array}\right]$ $\mathbf{T}_6= \left[\begin{array}{cc} -0.7 & 0\\ 0 & 0.8 \end{array}\right]$ $\vec{\mathbf{q}}_6=\mathbf{T}_6\cdot \vec{\mathbf{q}}_0= \left[\begin{array}{cc} -0.7 & 0\\ 0 & 0.8 \end{array}\right] \cdot \left[\begin{array}{c}1\\2\end{array}\right]= \left[\begin{array}{c}-0.7\\1.6\end{array}\right]$