Difference between revisions of "Transformations"
| Line 8: | Line 8: | ||
</math> | </math> | ||
| − | + | The basic transformation matrix is an identity matrix, which corresponds to an empty transformation. So an identity matrix as transformation matrix results in the original vector no matter how many dimensions the vector has. The following equations show this for two and three dimensions:<br/> | |
:<math>\begin{align} | :<math>\begin{align} | ||
\vec{\mathbf{p}}_1&=&\mathbf{I}_2\cdot\vec{\mathbf{p}}_0&=& | \vec{\mathbf{p}}_1&=&\mathbf{I}_2\cdot\vec{\mathbf{p}}_0&=& | ||
Revision as of 14:33, 26 May 2014
| ← Back: Adjugate Formula | Overview: Transformations | Next: Translation → |
In this article general transformations used in the context of robotics and the underlying mathematics are described.
Transformations are applied to vectors or coordinates in vector notation, respectively. All types of transformations can be achieved by matrix multiplication. To transform a vector 
to 
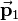, has to be multilplied by the transformation matrix 
:
The basic transformation matrix is an identity matrix, which corresponds to an empty transformation. So an identity matrix as transformation matrix results in the original vector no matter how many dimensions the vector has. The following equations show this for two and three dimensions:
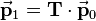
![\begin{align}
\vec{\mathbf{p}}_1&=&\mathbf{I}_2\cdot\vec{\mathbf{p}}_0&=&
\left[\begin{array}{cc}
1&0\\
0&1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0\\
y_0
\end{array}\right]&=&
\left[\begin{array}{c}
1\cdot x_0+0\cdot y_0\\
0\cdot y_0+1\cdot y_0
\end{array}\right]&=&
\left[\begin{array}{c}
x_0\\
y_0
\end{array}\right]&=&
\vec{\mathbf{p}}_0 \\
\vec{\mathbf{p}}_1&=&\mathbf{I}_3\cdot\vec{\mathbf{p}}_0&=&
\left[\begin{array}{ccc}
1&0&0\\
0&1&0\\
0&0&1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0\\
y_0\\
z_0
\end{array}\right]&=&
\left[\begin{array}{c}
1\cdot x_0+0\cdot y_0+0\cdot z_0\\
0\cdot y_0+1\cdot y_0+0\cdot z_0\\
0\cdot y_0+0\cdot y_0+1\cdot z_0
\end{array}\right]&=&
\left[\begin{array}{c}
x_0\\
y_0\\
z_0
\end{array}\right]&=&
\vec{\mathbf{p}}_0
\end{align}](/wiki/robotics/images/math/f/b/f/fbfe5b03c247d0fc135c0473666f4e42.png)
By modifying the components of the The different types of transformations are presented in the following subarticles:
