Matrix inversion

← Back: Minors and cofactors

Overview: Matrix inversion

Next: Gauß-Jordan-Algorithm →

The inverse of an n-by-n square matrix 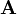$\mathbf{A}$ is denoted as 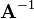$\mathbf{A}^{-1}$ and defined such that

$\mathbf{A}\mathbf{A}^{-1}=\mathbf{A}^{-1}\mathbf{A}=\mathbf{I}_n$

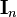where $\mathbf{I}_n$ is the n-by-n identity matrix.

Prerequesite for the inversion is, that 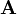$\mathbf{A}$ is an n-by-n square matrix and that 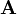$\mathbf{A}$ is regular. Regular means that the row and column vectors are linearly independent and so the determinant is nonzero:

$det(\mathbf{A})\ne0$

Otherwise the matrix is called singular.

Before determining the inverse of a matrix it is always useful to compute the determinant and check whether the matrix is regular or singular. If it is singular it is not possible to determine the inverse because there is no inverse. The following two subarticles describe two of the common procedures to determine the inverse of a matrix.

1. Gauß-Jordan-Algorithm
2. Adjugate Formula

Transformation matrices have a special structure, that is described in the transformations chapter. For this special matrix structure an easier method to invert the matrix exists. This method is presented in

      3. Inverse transformation.

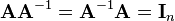
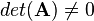
Example: inverse of a 2-by-2 matrix This is a simple example for the inverse of a 2-by-2 matrix: $\mathbf{A}_2 = \left[\begin{array}{cc} 2 & 3\\ 1 & 2 \end{array}\right] ,\quad {\mathbf{A}_2}^{-1} = \left[\begin{array}{cc} 2 & -3\\ -1 & 2 \end{array}\right]$ $\begin{align} {\mathbf{A}_2}{\mathbf{A}_2}^{-1} &= \left[\begin{array}{cc} 2 & 3\\ 1 & 2 \end{array}\right]\cdot \left[\begin{array}{cc} 2 & -3\\ -1 & 2 \end{array}\right]\\&= \left[\begin{array}{cc} 2\cdot2+3\cdot(-1) & 2\cdot(-3)+3\cdot2\\ 1\cdot2+2\cdot(-1) & 1\cdot(-3)+2\cdot2 \end{array}\right]\\&= \left[\begin{array}{cc} 4-3 & -6+6\\ 2-2 & -3+4 \end{array}\right]\\&= \left[\begin{array}{cc} {\color{Green}\mathbf{1}} & 0\\ 0 & {\color{Green}\mathbf{1}} \end{array}\right]= \mathbf{I}_2 \end{align}$

Example: inverse of a 3-by-3 matrix This is an example for the inverse of a 3-by-3 matrix: $\mathbf{A}_3 = \left[\begin{array}{ccc} 1&0&1\\ 3&1&0\\ 1&0&2 \end{array}\right] ,\quad {\mathbf{A}_3}^{-1} = \left[\begin{array}{ccc} 2&0&-1\\ -6&1&3\\ -1&0&1 \end{array}\right]$ $\begin{align} {\mathbf{A}_3}{\mathbf{A}_3}^{-1} &= \left[\begin{array}{ccc} 1&0&1\\ 3&1&0\\ 1&0&2 \end{array}\right]\cdot \left[\begin{array}{ccc} 2&0&-1\\ -6&1&3\\ -1&0&1 \end{array}\right]\\&= \left[\begin{array}{ccc} 1\cdot2+0\cdot(-6)+1\cdot(-1) & 1\cdot0+0\cdot1+1\cdot0 & 1\cdot(-1)+0\cdot3+1\cdot1\\ 3\cdot2+1\cdot(-6)+0\cdot(-1) & 3\cdot0+1\cdot1+0\cdot0 & 3\cdot(-1)+1\cdot3+0\cdot1\\ 1\cdot2+0\cdot(-6)+2\cdot(-1) & 1\cdot0+0\cdot1+2\cdot0 & 1\cdot(-1)+0\cdot3+2\cdot1 \end{array}\right]\\&= \left[\begin{array}{ccc} 2+0-1 & 0+0+0 & -1+0+1\\ 6-6+0 & 0+1+0 & -3+3+0\\ 2+0-2 & 0+0+0 & -1+0+2 \end{array}\right]\\&= \left[\begin{array}{ccc} {\color{Green}\mathbf{1}} & 0 & 0\\ 0 & {\color{Green}\mathbf{1}} & 0\\ 0 & 0 & {\color{Green}\mathbf{1}} \end{array}\right]= \mathbf{I}_3 \end{align}$

Example: inverse of a 4-by-4 matrix This example is a proof of equation 3.40 in the robotics script (see page 3-61): $^R\mathbf{T}_N = \left[\begin{array}{cccc} 0 & 1 & 0 & 2a\\ 0 & 0 & -1 & 0\\ -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right] ,\quad {^R\mathbf{T}_N}^{-1} = \left[\begin{array}{cccc} 0 & 0 & -1 & 0\\ 1 & 0 & 0 & -2a\\ 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]$ $\begin{align} {^R\mathbf{T}_N}{^R\mathbf{T}_N}^{-1} &= \left[\begin{array}{cccc} 0 & 1 & 0 & 2a\\ 0 & 0 & -1 & 0\\ -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]\cdot \left[\begin{array}{cccc} 0 & 0 & -1 & 0\\ 1 & 0 & 0 & -2a\\ 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]\\&= \left[\begin{array}{cccc} 0\cdot0+1\cdot1+0\cdot0+2a\cdot0 & 0\cdot0+1\cdot0+0\cdot(-1)+2a\cdot0 & 0\cdot(-1)+1\cdot0+0\cdot0+2a\cdot0 & 0\cdot0+1\cdot(-2a)+0\cdot0+2a\cdot1\\ 0\cdot0+0\cdot1+(-1)\cdot0+0\cdot0 & 0\cdot0+0\cdot0+(-1)\cdot(-1)+0\cdot0 & 0\cdot(-1)+0\cdot0+(-1)\cdot0+0\cdot0 & 0\cdot0+0\cdot(-2a)+(-1)\cdot0+0\cdot1\\ (-1)\cdot0+0\cdot1+0\cdot0+0\cdot0 & (-1)\cdot0+0\cdot0+0\cdot(-1)+0\cdot0 & (-1)\cdot(-1)+0\cdot0+0\cdot0+0\cdot0 & (-1)\cdot0+0\cdot(-2a)+0\cdot0+0\cdot1\\ 0\cdot0+0\cdot1+0\cdot0+1\cdot0 & 0\cdot0+0\cdot0+0\cdot(-1)+1\cdot0 & 0\cdot(-1)+0\cdot0+0\cdot0+1\cdot0 & 0\cdot0+0\cdot(-2a)+0\cdot0+1\cdot1\\ \end{array}\right]\\&= \left[\begin{array}{cccc} {\color{Green}\mathbf{1}} & 0 & 0 & 0\\ 0 & {\color{Green}\mathbf{1}} & 0 & 0\\ 0 & 0 & {\color{Green}\mathbf{1}} & 0\\ 0 & 0 & 0 & {\color{Green}\mathbf{1}} \end{array}\right]= \mathbf{I}_4 \end{align}$