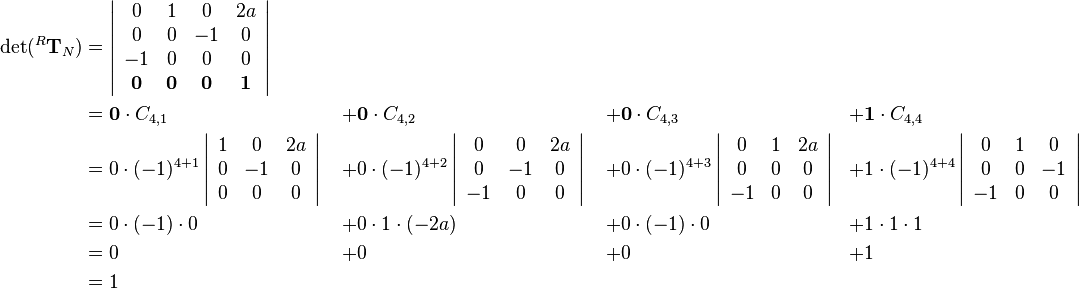Determinant of a matrix
| ← Back: Multiplication of matrices | Overview: Matrices | Next: Minors and cofactors → |
|
There are exercises as selftest for this article. |
The determinant can be computed for an n-by-n square matrix. In the context of matrices the determinant of a matrix is a special function that assigns a scalar value to the matrix. It is denoted with 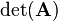 or in matrix structure with vertical lines:
or in matrix structure with vertical lines:
Considering a matrix as a linear system the determinant provides information about its solvability. If the determinant is nonzero the linear system is clearly solvable. This feature is also important for matrix inversion.
Properties
The determinant is a multiplicative mapping, such that
for all n-by-n square matrices 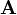 and
and 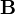 .
.
It holds for all n-by-n square matrices 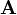 and all scalar values
and all scalar values  :
:
A matrix 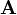 and its transposed have the same determinant:
and its transposed have the same determinant:
The determinant of an identity matrix is always 1:
2-by-2 matrices
For a 2-by-2 matrix the determinant can easily computed as follows:
|
3-by-3 matrices
For 3-by-3 matrices there is a formula called Rule of Sarrus to compute the determinant. The first two columns of the matrix are noted anew on the right of matrix. Then six diagonals are formed that describe the arithmetic operations to be performed:
The sum of the diagonal elements then forms the determinant:
The Khan Academy[1] provides a good video [2] where this formula is explained. Please watch the video for further information about the computation of the determinant of a 3-by-3 matrix.
|
4-by-4 matrices
One possibility to compute the determinant of a 4-by-4 matrix is a formula that uses the minors and cofactors of a matrix. Please read the article about minors and cofactors before you continue with this article. First one row or column has to be choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant. If a column 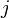 is choosen, it holds:
is choosen, it holds:
And if a row 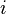 is choosen:
is choosen:
This example describes the computation of the determinant of the transformation matrix It is always useful to choose a row or column with many zero values so that the corresponding products are omitted and the cofactors have not to be computed. For the matrix |
References
- ↑ https://www.khanacademy.org/ Khan Academy
- ↑ https://www.khanacademy.org/.../finding-the-determinant-of-a-3x3-matrix-method-1 Determinant of a 3-by-3 matrix
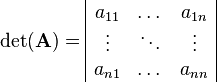
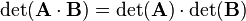
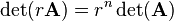
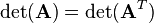

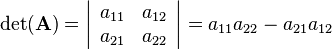
![\det(\mathbf{A}_2)=
\det
\left[\begin{array}{cc}
2&3\\
1&2
\end{array}\right] =
\left|\begin{array}{cc}
2&3\\
1&2
\end{array}\right|=
2\cdot 2-3\cdot 1=
4-3=1](/wiki/robotics/images/math/f/5/f/f5fabf30e45506e0a9bfa83a74dabb24.png)

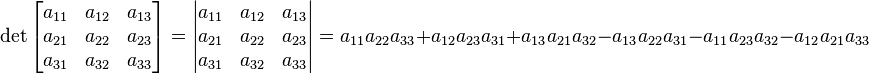
![\det(\mathbf{A}_3)=
\det
\left[\begin{array}{ccc}
1&0&1\\
3&1&0\\
1&0&2
\end{array}\right] =
\left|\begin{array}{ccc}
1&0&1\\
3&1&0\\
1&0&2
\end{array}\right|=
1\cdot1\cdot2+0\cdot0\cdot1+1\cdot3\cdot0-1\cdot1\cdot1-1\cdot0\cdot0-0\cdot2\cdot3)=2+0+0-1-0-0=1](/wiki/robotics/images/math/d/f/9/df97ca317b69108f5870c9e6b487d31d.png)

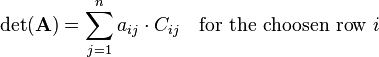
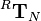 that is introduced in the robotics script in chapter 3 on page 3-37 and used on the following pages.
that is introduced in the robotics script in chapter 3 on page 3-37 and used on the following pages.
![^R\mathbf{T}_N =
\left[\begin{array}{cccc}
0 & 1 & 0 & 2a\\
0 & 0 & -1 & 0\\
-1 & 0 & 0 & 0\\
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/8/5/e/85e5abe5247392c6a2634922b8382d3d.png)