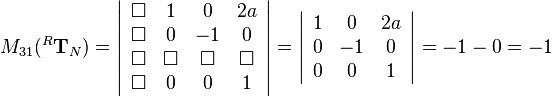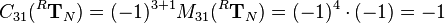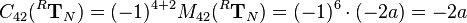Minors and cofactors
From Robotics
| ← Back: Determinant of a matrix | Overview: Matrices | Next: Matrix inversion → |
The minor 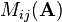 of an n-by-n square matrix
of an n-by-n square matrix 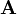 is the determinant of a smaller square matrix obtained by removing the row
is the determinant of a smaller square matrix obtained by removing the row 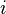 and the column
and the column 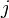 from
from 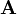 .
.
Multiplying the minor with 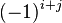 results in the cofactor
results in the cofactor 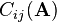 :
:
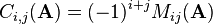
The minors The corresponding cofactors in that case are |
This example uses the transformation matrix The minors
|
![\mathbf{A}_3 =
\left[\begin{array}{ccc}
1&0&1\\
3&1&0\\
1&0&2
\end{array}\right]](/wiki/robotics/images/math/4/7/f/47ff3b29442735c862d2f12e20505fa0.png)
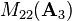 and
and 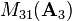 for example are defined as
for example are defined as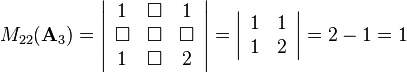
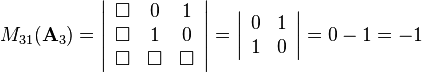
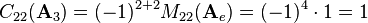
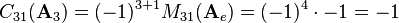
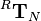 that is introduced in the robotics script in chapter 3 on page 3-37 and used on the following pages.
that is introduced in the robotics script in chapter 3 on page 3-37 and used on the following pages.
![^R\mathbf{T}_N =
\left[\begin{array}{cccc}
0 & 1 & 0 & 2a\\
0 & 0 & -1 & 0\\
-1 & 0 & 0 & 0\\
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/8/5/e/85e5abe5247392c6a2634922b8382d3d.png)
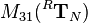 and
and 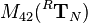 for example are defined as
for example are defined as