Gauß-Jordan-Algorithm

← Back: Matrix inversion

Overview: Matrix inversion

Next: Adjugate Formula →

The Gauß-Jordan-Algorithm was developed to solve systems of linear equations. But it can also be used to determine the inverse of an n-by-n square matrix.

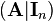The algorithm is based on the formula $\mathbf{A}\mathbf{A}^{-1}=\mathbf{I}_n$. First the block matrix $(\mathbf{A}|\mathbf{I}_n)$ is build. On this matrix the Gauß-Jordan-Algorithm is applied. By using various conversion steps like interchanging of rows and addtition of factorized rows to other rows the block matrix is converted so that the left block equals the identity matrix $\mathbf{I}_n$. The right block then corresponds to the inverse of $\mathbf{A}$.

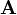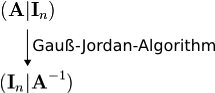
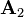Example: Gauß-Jordan-Algorithm for a 2-by-2 matrix This example describes the application of the Gauß-Jordan-Algorithm to compute the inverse of $\mathbf{A}_2$, which is already used for the example in the main article of matrix inversion. $\begin{align} \mathbf{A}_2 = &\left[\begin{array}{cc} 2 & 3\\ 1 & 2 \end{array}\right]\\ \\ (\mathbf{A}_2|\mathbf{I}_2) = &\left[\begin{array}{cc|cc} 2 & 3 & 1 & 0\\ 1 & 2 & 0 & 1 \end{array}\right] \begin{array}{c} \text{substract row II}\\ \\ \end{array}\\ &\qquad\quad\Downarrow\\ &\left[\begin{array}{cc|cc} 1 & 1 & 1 & -1\\ 1 & 2 & 0 & 1 \end{array}\right] \begin{array}{c} \\ \text{substract row I} \end{array}\\ &\qquad\quad\Downarrow\\ &\left[\begin{array}{cc|cc} 1 & 1 & 1 & -1\\ 0 & 1 & -1 & 2 \end{array}\right] \begin{array}{c} \text{substract row II}\\ \\ \end{array}\\ &\qquad\quad\Downarrow\\ &\left[\begin{array}{cc|cc} {\color{Green}\mathbf{1}} & 0 & 2 & -3\\ 0 & {\color{Green}\mathbf{1}} & -1 & 2 \end{array}\right] \\ &\qquad\mathbf{I}_2\qquad\mathbf{A}_2^{-1}\\ \\ \mathbf{A}_2^{-1} = &\left[\begin{array}{cc} 2 & -3\\ -1 & 2 \end{array}\right] \end{align}$ For a proof please have a look at the example in the main article of matrix inversion.

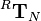Example: Gauß-Jordan-Algorithm for a 4-by-4 matrix This example describes the computation of the inverse of the transform matrix $^R\mathbf{T}_N$ that is introduced in the script on page 3-37 and used on the following pages. $\begin{align} ^R\mathbf{T}_N = &\left[\begin{array}{cccc} 0 & 1 & 0 & 2a\\ 0 & 0 & -1 & 0\\ -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]\\ \\ (\mathbf{A}_e|\mathbf{I}_4) = &\left[\begin{array}{cccc|cccc} 0 & 1 & 0 & 2a & 1 & 0 & 0 & 0\\ 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \end{array}\right] \begin{array}{c} \\ \updownarrow\text{interchange row II and row III}\\ \\ \end{array}\\ &\qquad\qquad\quad\quad\Downarrow\\ &\left[\begin{array}{cccc|cccc} 0 & 1 & 0 & 2a & 1 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & -1 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \end{array}\right] \begin{array}{c} \\ \\ \text{multiply by (-1)}\\ \\ \end{array}\\ &\qquad\qquad\quad\quad\Downarrow\\ &\left[\begin{array}{cccc|cccc} 0 & 1 & 0 & 2a & 1 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \end{array}\right] \begin{array}{c} \updownarrow\text{interchange row I and row II}\\ \\ \\ \end{array}\\ &\qquad\qquad\quad\quad\Downarrow\\ &\left[\begin{array}{cccc|cccc} -1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 2a & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \end{array}\right] \begin{array}{c} \text{multiply by (-1)}\\ \\ \\ \\ \end{array}\\ &\qquad\qquad\quad\quad\Downarrow\\ &\left[\begin{array}{cccc|cccc} 1 & 0 & 0 & 0 & 0 & 0 & -1 & 0\\ 0 & 1 & 0 & 2a & 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \end{array}\right] \begin{array}{c} \\ \text{substract (-2a) times row IV}\\ \\ \\ \end{array}\\ &\qquad\qquad\quad\quad\Downarrow\\ &\left[\begin{array}{cccc|cccc} {\color{Green}\mathbf{1}} & 0 & 0 & 0 & 0 & 0 & -1 & 0\\ 0 & {\color{Green}\mathbf{1}} & 0 & 0 & 1 & 0 & 0 & -2a\\ 0 & 0 & {\color{Green}\mathbf{1}} & 0 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & {\color{Green}\mathbf{1}} & 0 & 0 & 0 & 1 \end{array}\right]\\ &\qquad\quad\mathbf{I}_4\qquad\qquad\qquad{^R\mathbf{T}_N}^{-1}\\ \\ {^R\mathbf{T}_N}^{-1} = &\left[\begin{array}{cccc} 0 & 0 & -1 & 0\\ 1 & 0 & 0 & -2a\\ 0 & -1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right] \end{align}$ For a proof please have a look at the example in the main article of matrix inversion.