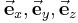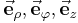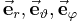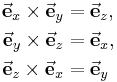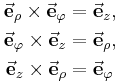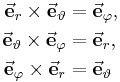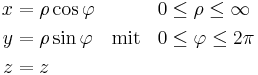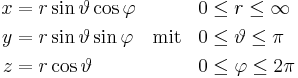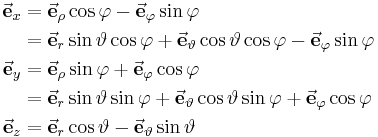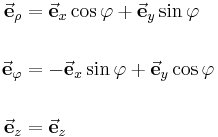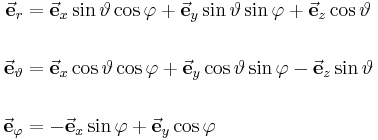Formelsammlung Koordinatensysteme: Unterschied zwischen den Versionen

Aus GET A
Wechseln zu: Navigation, Suche
Zeile 60: Zeile 60:
 
<math>\begin{align}
 
<math>\begin{align}
 
\vec{\mathbf{e}}_x &= \vec{\mathbf{e}}_{\rho}\cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\
 
\vec{\mathbf{e}}_x &= \vec{\mathbf{e}}_{\rho}\cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\
−
                   &= \vec{\mathbf{e}}_r\sin{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_{\vartheta}  \cos{vartheta}  \cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\
+
                   &= \vec{\mathbf{e}}_r\sin{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_{\vartheta}  \cos{\vartheta}  \cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\
 
\vec{\mathbf{e}}_y &= \vec{\mathbf{e}}_{\rho}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\
 
\vec{\mathbf{e}}_y &= \vec{\mathbf{e}}_{\rho}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\
−
                   &= \vec{\mathbf{e}}_r\sin{\vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\vartheta}\cos{vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\
+
                   &= \vec{\mathbf{e}}_r\sin{\vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\vartheta}\cos{\vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\
  
 
\vec{\mathbf{e}}_z &= \vec{\mathbf{e}}_r\cos{\vartheta}-\vec{\mathbf{e}}_{\vartheta}\sin{\vartheta}\\
 
\vec{\mathbf{e}}_z &= \vec{\mathbf{e}}_r\cos{\vartheta}-\vec{\mathbf{e}}_{\vartheta}\sin{\vartheta}\\
 
\end{align}</math>
 
\end{align}</math>
−
 
 
|style="background-color:#dde6f3;text-align:center;"|
 
|style="background-color:#dde6f3;text-align:center;"|
 +
<math>\begin{align}\vec{\mathbf{e}}_{\rho} &= \vec{\mathbf{e}}_x\cos{\varphi}+\vec{\mathbf{e}}_y\sin{\varphi}\\
 +
\\
 +
\vec{\mathbf{e}}_{\varphi} &= -\vec{\mathbf{e}}_x\sin{\varphi}+\vec{\mathbf{e}}_y\cos{\varphi}\\
 +
\\               
 +
\vec{\mathbf{e}}_z &= \vec{\mathbf{e}}_z
 +
\end{align}</math>
 
|style="background-color:#c9d7ec;text-align:center;"|
 
|style="background-color:#c9d7ec;text-align:center;"|
−
 
+
<math>\begin{align}\vec{\mathbf{e}}_r &=  \vec{\mathbf{e}}_x\sin{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_y\sin{\vartheta}  \sin{\varphi}+\vec{\mathbf{e}}_z\cos{\vartheta}\\
−
 
+
\\
 +
\vec{\mathbf{e}}_{\vartheta} &= \vec{\mathbf{e}}_x\cos{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_y\cos{\vartheta}\sin{\varphi}-\vec{\mathbf{e}}_z\sin{\vartheta}\\
 +
\\
 +
\vec{\mathbf{e}}_{\varphi} &= -\vec{\mathbf{e}}_x\sin{\varphi}+\vec{\mathbf{e}}_y\cos{\varphi}
 +
\end{align}</math>
 
|-
 
|-
 
|style="background-color:#dde6f3"|Ortsvektor
 
|style="background-color:#dde6f3"|Ortsvektor

Version vom 28. August 2012, 10:55 Uhr

Kartesische Koordinaten

Zylinderkoordinaten

Kugelkoordinaten

Einheitsvektoren

\vec{\mathbf{e}}_x,\vec{\mathbf{e}}_y,\vec{\mathbf{e}}_z

\vec{\mathbf{e}}_{\rho},\vec{\mathbf{e}}_{\varphi},\vec{\mathbf{e}}_z

\vec{\mathbf{e}}_r, \vec{\mathbf{e}}_{\vartheta},\vec{\mathbf{e}}_{\varphi}

Kreuzprodukt

\begin{align} \vec{\mathbf{e}}_x\times\vec{\mathbf{e}}_y &=\vec{\mathbf{e}}_z,\\ \vec{\mathbf{e}}_y\times\vec{\mathbf{e}}_z &=\vec{\mathbf{e}}_x,\\ \vec{\mathbf{e}}_z\times\vec{\mathbf{e}}_x &=\vec{\mathbf{e}}_y \end{align}

\quad

\begin{align} \vec{\mathbf{e}}_{\rho}\times\vec{\mathbf{e}}_{\varphi} &=\vec{\mathbf{e}}_z,\\ \vec{\mathbf{e}}_{\varphi}\times\vec{\mathbf{e}}_z &=\vec{\mathbf{e}}_{\rho},\\ \vec{\mathbf{e}}_z \times\vec{\mathbf{e}}_{\rho} &=\vec{\mathbf{e}}_{\varphi} \end{align}

\begin{align} \vec{\mathbf{e}}_r\times\vec{\mathbf{e}}_{\vartheta} &= \vec{\mathbf{e}}_{\varphi},\\ \vec{\mathbf{e}}_{\vartheta}\times\vec{\mathbf{e}}_{\varphi} &= \vec{\mathbf{e}}_r,\\ \vec{\mathbf{e}}_{\varphi}\times\vec{\mathbf{e}}_r &= \vec{\mathbf{e}}_{\vartheta} \end{align}

Zusammenhang mit den kartesischen Koordinaten

\begin{align} x &=\rho\cos{\varphi} && && 0\leq\rho\leq\infty\\ y &=\rho\sin{\varphi} &&\text{mit}&& 0\leq\varphi\leq2\pi\\ z &=z \end{align}

\begin{align}x &=r\sin{\vartheta}\cos{\varphi} && && 0\leq r \leq\infty\\ y &=r\sin{\vartheta}\sin{\varphi} &&\text{mit}&& 0\leq\vartheta\leq \pi\\ z &=r\cos{\vartheta} && && 0\leq\varphi\leq 2\pi \end{align}

Umrechnungen

\begin{align} \vec{\mathbf{e}}_x &= \vec{\mathbf{e}}_{\rho}\cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\ &= \vec{\mathbf{e}}_r\sin{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_{\vartheta} \cos{\vartheta} \cos{\varphi}-\vec{\mathbf{e}}_{\varphi}\sin{\varphi}\\ \vec{\mathbf{e}}_y &= \vec{\mathbf{e}}_{\rho}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\ &= \vec{\mathbf{e}}_r\sin{\vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\vartheta}\cos{\vartheta}\sin{\varphi}+\vec{\mathbf{e}}_{\varphi}\cos{\varphi}\\ \vec{\mathbf{e}}_z &= \vec{\mathbf{e}}_r\cos{\vartheta}-\vec{\mathbf{e}}_{\vartheta}\sin{\vartheta}\\ \end{align}

\begin{align}\vec{\mathbf{e}}_{\rho} &= \vec{\mathbf{e}}_x\cos{\varphi}+\vec{\mathbf{e}}_y\sin{\varphi}\\ \\ \vec{\mathbf{e}}_{\varphi} &= -\vec{\mathbf{e}}_x\sin{\varphi}+\vec{\mathbf{e}}_y\cos{\varphi}\\ \\ \vec{\mathbf{e}}_z &= \vec{\mathbf{e}}_z \end{align}

\begin{align}\vec{\mathbf{e}}_r &= \vec{\mathbf{e}}_x\sin{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_y\sin{\vartheta} \sin{\varphi}+\vec{\mathbf{e}}_z\cos{\vartheta}\\ \\ \vec{\mathbf{e}}_{\vartheta} &= \vec{\mathbf{e}}_x\cos{\vartheta}\cos{\varphi}+\vec{\mathbf{e}}_y\cos{\vartheta}\sin{\varphi}-\vec{\mathbf{e}}_z\sin{\vartheta}\\ \\ \vec{\mathbf{e}}_{\varphi} &= -\vec{\mathbf{e}}_x\sin{\varphi}+\vec{\mathbf{e}}_y\cos{\varphi} \end{align}

Ortsvektor
Betrag des Ortsvektors
vektorielles Wegelement
Volumenelement
vektorielles Flächenelement
Abgerufen von „https://getwww.uni-paderborn.de/wiki/geta/index.php?title=Formelsammlung_Koordinatensysteme&oldid=4353“