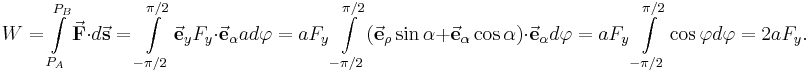Das Linienintegral
To-do:
- Einleitung etwas plausibler (es gibt doch genügend Beispiele)
- Formulierungen überarbeiten (insbes. fett)
In der Elektrotechnik hat man häufig das Problem, dass die zu integrierende Größe einer Anordnung nicht geradlinig verläuft (Formulierung). Ein Beispiel hierfür ist die Berechnung des Potentials zwischen zwei Punkten mit Hilfe des elektrischen Feldes (welches auch inhomogen sein kann, sodass der Weg zwischen den Punkten nicht mehr beliebig wählbar ist (unklar!)). Ist der Weg nun gebogen, oder anders verformt braucht man das Linienintegral, um solche Anordnungen berechnen zu können. Ein anderes Anwendungsbeispiel ist die Ermittlung der elektrischen Energie über die Integralform.
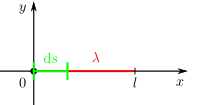
Um solch ein Linienintegral zu bestimmen, ist die Betrachtung über die infinitesimalen Wegelemente hilfreich:
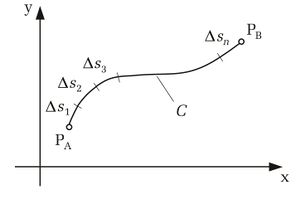
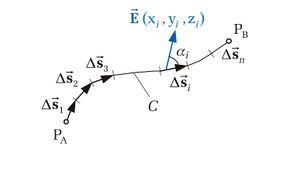
Hier wählt man eine Funktion von z. B. zwei Veränderlichen f(x,y) entlang eines zwischen den Endpunkten  und
und  liegenden Kurvenbogens der Kontur C. Integrale können von einer Variablen, aber genauso gut von zwei oder mehr Veränderlichen abhängen. Solche Dinge ergeben sich meistens aus den konkreten Aufgabenstellungen. Für diese Betrachtung wird der Kurvenbogen C in n Teilstücke
liegenden Kurvenbogens der Kontur C. Integrale können von einer Variablen, aber genauso gut von zwei oder mehr Veränderlichen abhängen. Solche Dinge ergeben sich meistens aus den konkreten Aufgabenstellungen. Für diese Betrachtung wird der Kurvenbogen C in n Teilstücke  mit i = 1 ... n zerlegt und auf jedem Teilstück wird ein Punkt
mit i = 1 ... n zerlegt und auf jedem Teilstück wird ein Punkt 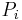 mit den Koordinaten
mit den Koordinaten 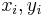 bestimmt.
bestimmt.
Damit man einen Näherungswert für das Linienintegral bekommt, bildet man zunächst das Produkt aus den Bogenlängen 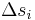 und den Funktionswerten
und den Funktionswerten 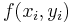 an den Punkten
an den Punkten 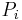 . Danach werden diese Produkte aufsummiert und man erhält so die Näherung:
. Danach werden diese Produkte aufsummiert und man erhält so die Näherung:
Da nicht nur nach einer ungefähren Approximation gefragt ist, sondern nach einer möglichst genauen Darstellung, bildet man den Grenzwert dieser Summe und lässt die Anzahl der Teilstücke n gegen Unendlich gehen, während die Ausdehnung der Bogenlängen gegen Null geht. Auf diese Weise erhält man eine sehr feine Unterteilung der Kontur C und die Summe geht gegen ihren Grenzwert (sofern er existiert und von der Wahl der Bogenlängen 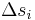 und den Punkten
und den Punkten 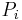 unabhängig ist). So ergibt sich das Linienintegral der Kontur C zwischen den Punkten
unabhängig ist). So ergibt sich das Linienintegral der Kontur C zwischen den Punkten 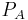 und
und 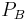 :
:
In diesem Beispiel wird eine Linienladung Linienladungen sind Ladungen entlang einer Kontur, deren Wert pro Streckenabschnitt schwanken kann. Um die gesamte Ladung zu berechnen, verwendet man das Linienintegral:
Im einfachsten Fall ist die Linienladung Dadurch wird das Integral einfach, da 2.Fall Etwas schwieriger wird es, wenn Dadurch muss die Funktion über die Länge der Linienladung integriert werden, um den Wert der Gesamtladung zu ermitteln. Formal wird dabei einfach die Funktion 3.Fall
Nun betrachtet man eine Linienladung in der Form eines Viertelkreisbogens. Es sei nun wieder anzunehmen, dass die Linienladung Man hat nun zwei Möglichkeiten, um durch Integration die Gesamtladung zu ermitteln, da so, wie die Funktion in der Abbildung dargestellt ist, sie sowohl von x als auch von y abhängt. Zunächst kann man das Parametrisieren verwenden. Dabei beschreibt man x und y durch eine einzelne neue Variable. Dies ist allerdings etwas kompliziert, daher verwenden wir hier die Zylinderkoordinaten bzw. die Polarkoordinaten, um das System zu beschreiben, weil die Linienladung dann entlang der Koordinaten verläuft, und der Viertelkreisbogen nur noch von einer Koordinate Als ersten Schritt stellt man also den Viertelkreisbogen in Polarkoordinaten dar. Wir integrieren also, wie in der Abbildung zu sehen ist, von der positiven x-Achse, also Diese Umformung ist ebenso für die Einheit wichtig. Die Ladung hat die Einheit Mit diesen Vorbetrachten lässt sich folgendes Integral aufstellen: |
Das Linienintegral einer vektoriellen Größe
Im vorherigen ging es um die Integration skalarer Größen. Hat man aber beispielsweise ein elektrisches Feld  angelegt, betrachtet man nicht nur die Stärke, sondern auch die Richtung des Feldes im Raum. Um das berücksichtigen zu können, muss die Form des Linienintegrals angepasst werden. Deswegen hat man sowohl bei der Funktion
angelegt, betrachtet man nicht nur die Stärke, sondern auch die Richtung des Feldes im Raum. Um das berücksichtigen zu können, muss die Form des Linienintegrals angepasst werden. Deswegen hat man sowohl bei der Funktion 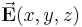 als auch bei dem Wegelement
als auch bei dem Wegelement 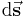 eine vektorielle Größe, da es in diesem Beispiel den Unterschied zwischen einer positiven, negativen oder gar keiner Spannung machen kann.
eine vektorielle Größe, da es in diesem Beispiel den Unterschied zwischen einer positiven, negativen oder gar keiner Spannung machen kann.
Zur Bestimmung des Linienintegrals einer vektoriellen Größe kann ebenso wie bei skalaren Größen das Integral über die infinitesimalen Wegelemente berechnet werden. Man verwendet nun wieder eine Kontur C, die zwischen den Punkten 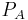 und
und 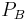 verläuft. Allerdings sind diesmal, die Wegelemente
verläuft. Allerdings sind diesmal, die Wegelemente 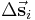 gerichtete Größen. Auch hier wird die Kontur in n Teilstücke
gerichtete Größen. Auch hier wird die Kontur in n Teilstücke 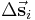 mit i = 1 ... n unterteilt und ein Punkt
mit i = 1 ... n unterteilt und ein Punkt 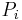 mit den Koordinaten
mit den Koordinaten 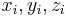 einer vektoriellen Größe
einer vektoriellen Größe 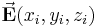 zugeordnet.
Um nun das Linienintegral berechnen zu können, muss das Skalarprodukt zwischen jedem Wegelement, dem dazugehörigen Funktionswert und dem eingeschlossenem Winkel
zugeordnet.
Um nun das Linienintegral berechnen zu können, muss das Skalarprodukt zwischen jedem Wegelement, dem dazugehörigen Funktionswert und dem eingeschlossenem Winkel 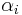 gebildet werden.
gebildet werden.
Summiert man nun ebenfalls alle Skalarprodukte auf und bildet gemäß der Gleichung des Linienintegrals der skalaren Größen den Grenzwert, erhält man für das Linienintegral einer vektoriellen Größe folgende Form:
Ein häufiger Anwendungsfall des Linienintegrals ergibt sich bei der Bestimmung der Spannung im elektrischen Feld.
Bildet man beispielsweise eine Kontur gemäß der Abbildung in einem homogenen, gleichgerichtetem elektrischen Feld erhält man folgendes Ringintegral:
Um dieses Integral zu lösen, können wir vier Fälle unterscheiden: Nun unterteilt man das Integral in diese vier Bereiche und bildet jeweils das Skalarprodukt: Daraus folgt: Durch die eingeschlossenen Rechten Winkel in den letzen beiden Fällen ergibt das Skalarprodukt Null und es bleibt nur noch übrig: Da hier die Strecken zwischen Dies ist eine wichtige Erkenntnis im elektrostatischen Feld: Das Ringintegral über ein homogenes, elektrisches Feld ergibt immer Null. |
Gesucht ist die Arbeit
die an einer Kugel verichtet wird, welche infolge einer Kraft Der Bewegungsvorgang wird im zylindrischen Koordinatensystem mit dem Ursprung im Mittelpunkt des Kreises beschrieben, dadurch bewegt sich die Kugel in Richtung wachsender Um die geleistete Arbeit W zu bestimmen, muss die Kraft in Komponenten zerlegt werden, da nur die in Richtung der Bewegung wirkende Kraftkomponente einen Beitrag zur Arbeit leistet. Eine Komponente wirkt in Richtung |
Multimediale Lehrmaterialien
|
http://www.dangries.com/Flash/IntegralSketch/IntegralSketch.html Applet zum Verständnis von Integralen http://www.uni-due.de/~matj00/bauws10/VorlBau100518.html Applet zum Verständnis von Integralen http://mathdl.maa.org/images/upload_library/4/vol4/kaskosz/antapp.html Applet: verschiedener Kurvenbeispiele und ihre Integrale (engl.) |
Hilfreiche Links
|
http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/lwolf/integralfkt/integralfkt1.html Interaktives Arbeitsblatt zur Integration http://web.mit.edu/8.02t/www/materials/modules/ReviewB.pdf Bebilderte Erklärung zu Kartesischen-, Kugel-, und Zylinderkoordinatensystemen und deren infinitesimalen Elementen (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Hempel, "Mathematische Grundlagen", Linienintegral, Universität Magdeburg
- TU Freiberg, "Parameter- und Kurvenintegrale", Script, 2010
| ← Zurück: Erweiterung der Integralrechnung:Übersicht | Übersicht: Erweiterung der Integralrechnung | Vorwärts: Das Flächenintegral → |
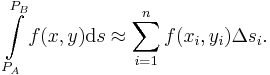
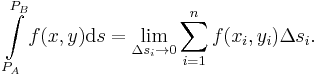
 betrachtet, die im folgenden mehrere Verläufe annimmt.
betrachtet, die im folgenden mehrere Verläufe annimmt.
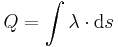
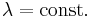

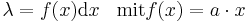
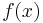 für
für 
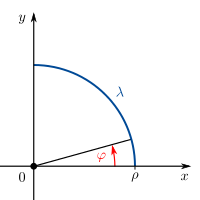
 abhängig ist. So wird die Rechnung durch Verwenden des neuen Koordinatensystems stark vereinfacht:
abhängig ist. So wird die Rechnung durch Verwenden des neuen Koordinatensystems stark vereinfacht:
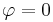 bis zur positiven y-Achse, also
bis zur positiven y-Achse, also 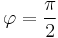 . Anschließend muss das
. Anschließend muss das 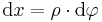
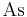 . Weil die Linienladung
. Weil die Linienladung  hat, muss die integrierte Größe die Einheit
hat, muss die integrierte Größe die Einheit 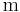 besitzen, damit die Gleichung stimmt. An vielen Stellen werden Winkel wie
besitzen, damit die Gleichung stimmt. An vielen Stellen werden Winkel wie 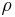 :
:
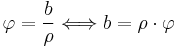
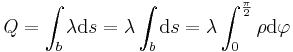
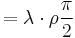
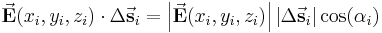
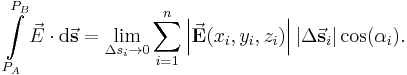
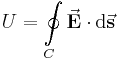

 bis
bis  , die mit dem Elektrischen Feld verläuft.
, die mit dem Elektrischen Feld verläuft. bis
bis  , die entgegen dem Elektrischen Feld verläuft.
, die entgegen dem Elektrischen Feld verläuft.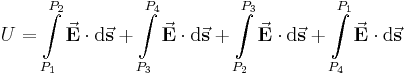
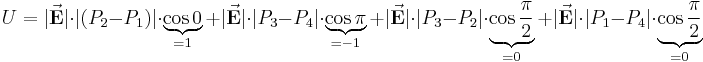
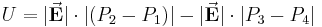
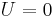
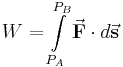 ,
,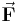 eine Laufrinne hinunterrollt. Die Laufrinne ist halbkreisförmig und spannt sich vom Anfangspunkt
eine Laufrinne hinunterrollt. Die Laufrinne ist halbkreisförmig und spannt sich vom Anfangspunkt 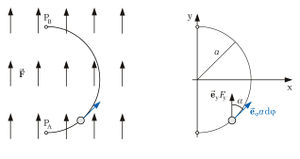
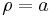 . So ist auf dem Halbkreis der Winkel
. So ist auf dem Halbkreis der Winkel 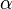 zwischen der Bewegungsrichtung
zwischen der Bewegungsrichtung 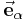 und der Kraftrichtung
und der Kraftrichtung 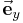 bekannt, da die vorgegebene Kraft sich am einfachsten mit einer kartesischen Komponente
bekannt, da die vorgegebene Kraft sich am einfachsten mit einer kartesischen Komponente 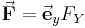 beschreiben lässt.
beschreiben lässt.
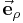 .
Nun benötigt man das Skalarprodukt aus der vektoriellen Kraft und dem gerichteten Wegelement, dessen Integration vom Anfangspunkt
.
Nun benötigt man das Skalarprodukt aus der vektoriellen Kraft und dem gerichteten Wegelement, dessen Integration vom Anfangspunkt