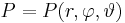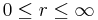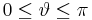Orthogonale Koordinatensysteme:Übersicht
To-do:
- Einleitung etwas plausibler (es gibt doch genügend Beispiele)
- Formulierungen überarbeiten (insbes. fett)
Einführung
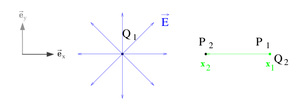
Da unterschiedliche Problemstellungen unterschiedlich komplexe Darstellungen erfordern, ist es sinnvoll verschiedene Koordinatensysteme zu verwenden. Möchte man beispielsweise die Kraftwirkungen unterschiedlicher Punktladungen aufeinander berechnen, verwendet man ein Koordinatensystem, um die Punktladungen in relativer Position zueinander angeben zu können. Dafür muss, egal welches Koordinatensystem verwendet wird, immer ein Bezugspunkt fest gewählt werden. An welcher Stelle sich der Bezugspunkt befindet ist willkürlich. Wählt man diesen Bezugspunkt geschickt, vereinfacht sich dadurch jedoch die anschließende Berechnung.
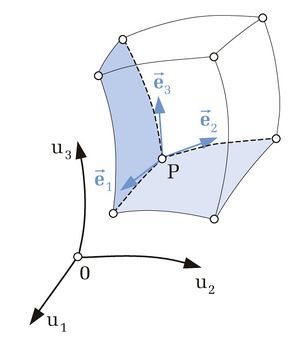
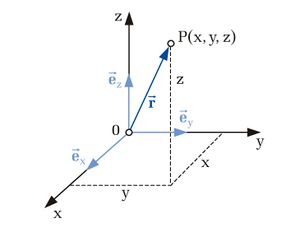
Mithilfe von Koordinatensystemen, kann ein Punkt P durch einen Vektor beschrieben werden, der von dem Bezugspunkt zu dem Punkt P zeigt. Der Vektor wird dann entweder mit Hilfe der Koordinatendarstellung oder der Komponentendarstellung beschrieben. Die Komponenten werden dabei in der Regel so gewählt, dass sie zueinander orthogonal sind, also senkrecht aufeinander stehen.
Bei den drei in den folgenden Abschnitten betrachteten Fällen, nämlich den kartesischen Koordinaten, den Zylinderkoordinaten und den Kugelkoordinaten, handelt es sich um orthogonale Koordinatensysteme. Dabei stehen die Einheitsvektoren 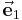 ,
, 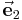 ,
, 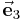 senkrecht aufeinander und weisen immer in die Richtung wachsender Koordinatenwerte. Setzt man die Einheitsvektoren in das Skalarprodukt ein, ergibt sich durch die Orthogonalität automatisch:
senkrecht aufeinander und weisen immer in die Richtung wachsender Koordinatenwerte. Setzt man die Einheitsvektoren in das Skalarprodukt ein, ergibt sich durch die Orthogonalität automatisch:
Außerdem sind die hier behandelten Koordinatensysteme so genannte Rechtssysteme, das heißt, dass das Vektorprodukt zweier aufeinander folgender Einheitsvektoren den jeweils nächsten Einheitsvektor ergeben muss, dies kann auch durch die [Rechte Hand Regel1] veranschaulicht werden:
Übersicht
| Das kartesische Koordinatensystem
Bei dem kartesischen Koordinatensystem sind die Koordinatenachsen geradlinig und orthogonal angeordnet, so dass die Achsen ein Rechtssystem bilden, welches durch die Rechte Handregel 1 beschrieben werden kann. Der Schnittpunkt der Achsen wird Koordinatenursprung genannt. Die Einheitsvektoren sind parallel zu den Achsen angeordnet und zeigen immer in Richtung wachsender Koordinatenwerte, daher sind die Einheitsvektoren auch unabhängig von der Position des Punktes im Raum und zeigen immer dieselbe Richtung an. |
|
|
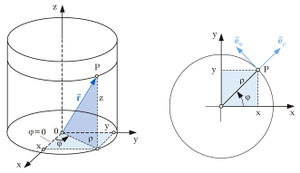
| Zylinderkoordinaten
Bei den Zylinderkoordinaten bleibt die z-Koordinate im Vergleich zu den kartesischen Koordinaten unverändert (hä?). In der x-y-Ebene werden allerdings die Koordinaten |
|
|
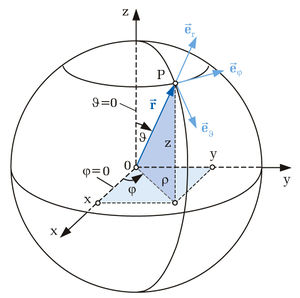
| Kugelkoordinaten
Bei dem Kugelkoordinatensystem bestimmt r den Abstand zum Ursprung. |
|
|
| Krummlinige orthogonale Koordinatensysteme |
|
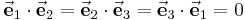
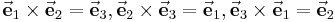
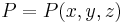
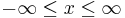

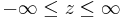
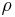 und
und  verwendet.
verwendet. 
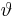 , er wird zwischen der positiven z-Achse und dem Punkt P gemessen. Auch hier gilt, alle Punkte mit dem selben Winkel
, er wird zwischen der positiven z-Achse und dem Punkt P gemessen. Auch hier gilt, alle Punkte mit dem selben Winkel