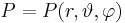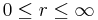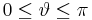Orthogonale Koordinatensysteme:Übersicht: Unterschied zwischen den Versionen
(→Einführung) |
(→Übersicht) |
||
| (257 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == Einführung == | + | {{Navigation|before=[[Formelsammlung zur Vektorrechnung]]|overview=[[Orthogonale Koordinatensysteme:Übersicht|Orthogonale Koordinatensysteme]]|next=[[Kartesische Koordinaten]]}} |
| − | + | ==Einführung== | |
| + | Koordinatensysteme werden zur eindeutigen Positionsbeschreibung von Punkten und Anordnungen (z. B. Ladungen oder stromführende Leiter) im Raum verwendet und ermöglichen erst die eindeutige Formulierung von [[Vektorrechnung:Übersicht|Vektoren]]. Weiterhin lassen sich ortsabhängige Größen wie beispielsweise elektrische und magnetische Felder beschreiben. In der Lehrverstaltung sind neben den bekannten [[Kartesische Koordinaten|kartesischen Koordinaten]] besonders [[Zylinderkoordinaten|Zylinder-]] und [[Kugelkoordinaten]] von Bedeutung. Auch bei diesen beiden Koordinatensystemen dient das kartesische Koordinatensystem jedoch immer als Referenz. In der Regel ist es vorteilhaft, ein auf die jeweilige Problemstellung „zugeschnittenes“ Koordinatensystem zu verwenden. Das elektrische Feld einer Punktladung <math>Q</math> ist beispielsweise radialsymmetrisch und der Betrag hängt ausschließlich vom Abstand <math>r</math> zur Punktladung ab, so dass sich die Verwendung von [[Kugelkoordinaten]] anbietet. Mit Hilfe eines entsprechenden [[Einheitsvektor|Einheitsvektors]] lässt sich die elektrische Feldstärke wie folgt angeben: | ||
| + | :<math> | ||
| + | \vec{\textbf{E}} = \dfrac{Q}{4\pi\varepsilon_0 r^2}\, \vec{\textbf{e}}_r | ||
| + | </math> | ||
| + | Die äquivalente Beschreibung in kartesischen Koordinaten ist weniger kompakt und lautet wie folgt (vgl. [[Formelsammlung Koordinatensysteme]]): | ||
| + | :<math> | ||
| + | \vec{\textbf{E}} = \dfrac{Q}{4\pi\varepsilon_0 (x^2+y^2+z^2)}\, (\vec{\textbf{e}}_x \sin\vartheta\cos\varphi +\vec{\textbf{e}}_y \sin\vartheta\sin\varphi +\vec{\textbf{e}}_z\cos\vartheta) | ||
| + | </math> | ||
| + | Mit Hilfe von [[trigonometrische Funktionen|trigonometrischen Funktionen]] können auch die aus dem Kugelkoordinatensystem stammenden Winkel <math>\varphi</math> und <math>\vartheta</math> ersetzt werden, so dass die Gleichung nur noch von <math>x</math>, <math>y</math> und <math>z</math> abhängt. Dadurch wird der Ausdruck noch umfangreicher. Eine „geschickte“ Wahl des Koordinatensystems kann außerdem zu erheblichen Vereinfachungen führen, beispielsweise bei der Bestimmung von Feldgrößen auf Basis von [[Erweiterung der Integralrechnung:Übersicht|Mehrfachintegralen]]. Diesbezüglich ist es oft vorteilhaft, wenn der Koordinatenursprung – sofern frei wählbar – passend zu den Symmetrieeigenschaften einer Anordnung positioniert wird. | ||
| + | |||
| + | Bei den vorgestellten Koordinatensystemen handelt es sich um '''orthogonale Koordinatensysteme'''. Dabei stehen die in Richtung wachsender Koordinatenwerte zeigenden Einheitsvektoren senkrecht aufeinander. Werden diese allgemein mit <math>\vec{\textbf{e}}_1</math>, <math>\vec{\textbf{e}}_2</math> und <math>\vec{\textbf{e}}_3</math> bezeichnet, so folgt mit dem [[Skalarprodukt]]: | ||
| + | :<math> | ||
| + | \vec{\textbf{e}}_1 \cdot \vec{\textbf{e}}_2 = | ||
| + | \vec{\textbf{e}}_2 \cdot \vec{\textbf{e}}_3 = | ||
| + | \vec{\textbf{e}}_3 \cdot \vec{\textbf{e}}_1 = 0 | ||
| + | </math> | ||
| + | Da die [[Koordinatenlinien]] bei den [[Zylinderkoordinaten|Zylinder-]] und [[Kugelkoordinaten]] nicht geradlinig verlaufen, werden diese als '''krummlinige orthogonale Koordinatensysteme''' bezeichnet. Bei dem kartesischen Koordinatensystem handelt es sich also um ein geradliniges orthogonales Koordinatensystem. Darüber hinaus handelt es sich um [[Rechtssystem|Rechtssysteme]] (prinzipiell sind auch andere Konventionen möglich), so dass das [[Vektorprodukt]] von zwei aufeinander folgenden Einheitsvektoren den jeweils nächsten Einheitsvektor liefert: | ||
| + | :<math> | ||
| + | \vec{\textbf{e}}_1 \times \vec{\textbf{e}}_2 = \vec{\textbf{e}}_3,\quad | ||
| + | \vec{\textbf{e}}_2 \times \vec{\textbf{e}}_3 = \vec{\textbf{e}}_1,\quad | ||
| + | \vec{\textbf{e}}_3 \times \vec{\textbf{e}}_1 = \vec{\textbf{e}}_2 | ||
| + | </math> | ||
| + | Die nachfolgende Tabelle zeigt eine Übersicht der verschiedenen Koordinatensysteme. | ||
| + | <!-- | ||
| + | ==Einführung [alt]== | ||
| + | |||
| + | [[Datei:Punktladungen.svg|300px|right|thumb|Koordinatensysteme dienen zur eindeutigen Beschreibung von Positionen (z. B. von Punktladungen) im Raum.]] | ||
| + | Da unterschiedliche Problemstellungen unterschiedlich komplexe Darstellungen erfordern, ist es sinnvoll verschiedene Koordinatensysteme zu verwenden ('''Argumentation unschlüssig'''). Möchte man beispielsweise die Kraftwirkung mehrerer Punktladungen aufeinander berechnen, verwendet man ein Koordinatensystem, um die Punktladungen in relativer Position zueinander angeben zu können ('''besser: die Positionen werden relativ zueinander angegeben, nicht die Punktladungen selbst'''). Dafür wird, egal ('''besser: unabhängig davon''') welches Koordinatensystem verwendet wird, immer ein fester Bezugspunkt gewählt. An welcher Stelle sich der Bezugspunkt befindet ist willkürlich. Wählt man diesen Bezugspunkt geschickt, vereinfacht sich dadurch jedoch die anschließende Berechnung ('''und wann liegt eine geschickte Wahl vor? z. B. wenn im Ursprung'''). | ||
| − | + | Mithilfe von Koordinatensystemen kann die Position von einem Punkt ''P'' durch einen [[Einführung in die Vektorrechnung|Vektor]] beschrieben werden, der ausgehend von einem gewählten Bezugspunkt zu diesem Punkt ''P'' zeigt. Der Vektor wird dann entweder mit Hilfe der [[Komponentendarstellung von Vektoren#Koordinatendarstellung von Vektoren|Koordinatendarstellung]] oder der [[Komponentendarstellung von Vektoren| Komponentendarstellung]] beschrieben. Die Komponenten werden dabei in der Regel so gewählt, dass sie zueinander orthogonal sind, also senkrecht aufeinander stehen ('''richtig?'''). | |
| − | + | Bei den drei in den folgenden Abschnitten betrachteten Fällen, nämlich den kartesischen Koordinaten, den Zylinderkoordinaten und den Kugelkoordinaten, handelt es sich um orthogonale Koordinatensysteme. Dabei stehen die [[Einheitsvektoren]] <math>\vec{\textbf{e}}_\mathrm{1}</math>, <math>\vec{\textbf{e}}_\mathrm{2}</math>, <math>\vec{\textbf{e}}_\mathrm{3}</math> senkrecht aufeinander und weisen immer in die Richtung wachsender Koordinatenwerte. Setzt man die [[Einheitsvektoren]] in das [[Skalarprodukt]] ein, ergibt sich durch die '''Orthogonalität''' automatisch ('''Formulierung'''): | |
| − | : | + | :<math> |
| − | <math> | ||
\vec{\textbf{e}}_\mathrm{1} \cdot \vec{\textbf{e}}_\mathrm{2} = | \vec{\textbf{e}}_\mathrm{1} \cdot \vec{\textbf{e}}_\mathrm{2} = | ||
\vec{\textbf{e}}_\mathrm{2} \cdot \vec{\textbf{e}}_\mathrm{3} = | \vec{\textbf{e}}_\mathrm{2} \cdot \vec{\textbf{e}}_\mathrm{3} = | ||
\vec{\textbf{e}}_\mathrm{3} \cdot \vec{\textbf{e}}_\mathrm{1} = 0 | \vec{\textbf{e}}_\mathrm{3} \cdot \vec{\textbf{e}}_\mathrm{1} = 0 | ||
</math> | </math> | ||
| − | |||
| − | |||
| − | + | Außerdem sind die hier ('''wo ist hier?''') behandelten Koordinatensysteme so genannte [[Rechtssystem|Rechtssysteme]], das heißt, dass das [[Vektorprodukt]] zweier aufeinander folgender Einheitsvektoren den jeweils nächsten Einheitsvektor ergeben muss, dies kann auch durch die [[Rechte Hand Regel1]] veranschaulicht werden: | |
| − | : | + | :<math> |
| − | <math> | ||
\vec{\textbf{e}}_\mathrm{1} \times \vec{\textbf{e}}_\mathrm{2} = \vec{\textbf{e}}_\mathrm{3}, | \vec{\textbf{e}}_\mathrm{1} \times \vec{\textbf{e}}_\mathrm{2} = \vec{\textbf{e}}_\mathrm{3}, | ||
\vec{\textbf{e}}_\mathrm{2} \times \vec{\textbf{e}}_\mathrm{3} = \vec{\textbf{e}}_\mathrm{1}, | \vec{\textbf{e}}_\mathrm{2} \times \vec{\textbf{e}}_\mathrm{3} = \vec{\textbf{e}}_\mathrm{1}, | ||
\vec{\textbf{e}}_\mathrm{3} \times \vec{\textbf{e}}_\mathrm{1} = \vec{\textbf{e}}_\mathrm{2} | \vec{\textbf{e}}_\mathrm{3} \times \vec{\textbf{e}}_\mathrm{1} = \vec{\textbf{e}}_\mathrm{2} | ||
</math> | </math> | ||
| − | + | --> | |
| − | |||
| − | == Übersicht == | + | ==Übersicht== |
| − | {| cellpadding="10" | + | {|cellpadding="10" |
| + | |- | ||
| + | |style="background-color:#dde6f3;"|[[Kartesische Koordinaten]] | ||
| + | Bei dem kartesischen Koordinatensystem wird ein Punkt <math>P</math> im Raum durch die drei Koordinaten <math>x</math>, <math>y</math> und <math>z</math> beschrieben. Die Koordinatenachsen sind geradlinig und orthogonal zueinander angeordnet, so dass diese ein [[Rechtssystem]] bilden. Der Schnittpunkt der Achsen, an dem alle Koordinaten den Wert Null haben, wird Koordinatenursprung genannt. Die Einheitsvektoren zeigen immer in die Richtung der jeweils zugehörigen Achse und in Richtung wachsender Koordinatenwerte, so dass diese an jedem Punkt im Raum identisch sind. | ||
| + | |style="background-color:#c9d7ec;text-align:center;"| | ||
| + | <math>P=P(x,y,z)</math><br> | ||
| + | <math>-\infty\leq x\leq\infty</math><br> | ||
| + | <math>-\infty\leq y\leq\infty</math><br> | ||
| + | <math>-\infty\leq z\leq\infty</math> | ||
| + | |style="background-color:#dde6f3"|[[Image:Kartesische Koordinaten.png|center|miniatur|Kartesische Koordinaten]] | ||
|- | |- | ||
| − | |style="background-color:#dde6f3 | + | |style="background-color:#dde6f3"|[[Zylinderkoordinaten]] |
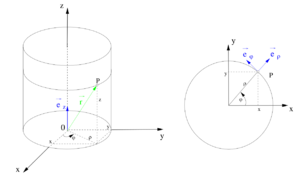
| − | Bei | + | Bei den Zylinderkoordinaten wird ein Punkt <math>P</math> im Raum durch die drei Koordinaten <math>\rho</math>, <math>\varphi</math> und <math>z</math> beschrieben. Dabei bleibt die <math>z</math>-Achse des kartesischen Koordinatensystems erhalten. <math>\rho</math> (je nach Quelle auch als <math>r</math> bezeichnet) gibt den Abstand zur <math>z</math>-Achse an und <math>\varphi</math> bezeichnet den Winkel zum betrachteten Punkt. Dabei wird <math>\varphi</math> ausgehend von der positiven <math>x</math>-Achse in Richtung der positiven <math>y</math>-Achse gezählt. Die Richtung der Einheitsvektoren <math>\vec{\textbf{e}}_\rho</math> und <math>\vec{\textbf{e}}_\varphi</math> hängt von der Position des betrachteten Punktes ab. Betrachtet man ausschließlich die <math>x</math>-<math>y</math>-Ebene ohne die <math>z</math>-Achse, so handelt es sich um Polarkoordinaten. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |style="background-color:#c9d7ec;text-align:center;"| | ||
| + | <math>P=P(\rho,\varphi,z)</math><br> | ||
| + | <math>0 \leq \rho \leq\infty</math><br> | ||
| + | <math>0 \leq \varphi < 2\pi</math><br> | ||
| + | <math>-\infty \leq z \leq\infty</math> | ||
| + | |style="background-color:#dde6f3"|[[Image:Zylinderkoordinaten.png|center|miniatur|Zylinderkoordinaten]] | ||
|- | |- | ||
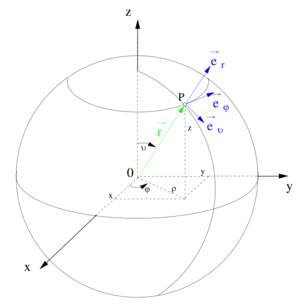
| − | |style="background-color:#dde6f3"|[[ | + | |style="background-color:#dde6f3"|[[Kugelkoordinaten]] |
| + | Bei dem Kugelkoordinatensystem wird ein Punkt <math>P</math> im Raum durch die drei Koordinaten <math>r</math>, <math>\vartheta</math> und <math>\varphi</math> beschrieben. Dabei bezeichnet <math>r</math> den Abstand des betrachteten Punktes vom Koordinatenursprung. <math>\vartheta</math> gibt den Winkel zwischen der positiven <math>z</math>-Achse und dem vom Ursprung zum betrachteten Punkt zeigenden Ortsvektor an. Der Winkel <math>\varphi</math> wird wie bei den Zylinderkoordinaten gezählt, also ausgehend von der positiven <math>x</math>-Achse in Richtung der positiven <math>y</math>-Achse. Die Richtung der Einheitsvektoren <math>\vec{\textbf{e}}_r</math>, <math>\vec{\textbf{e}}_\vartheta</math> und <math>\vec{\textbf{e}}_\varphi</math> hängt stets von der Position des betrachteten Punktes ab. Alle Punkte mit identischem <math>\vartheta</math> liegen auf einem „Breitengrad” und Punkte mit identischem <math>\varphi</math> liegen auf einem „Längengrad“. | ||
| + | |style="background-color:#c9d7ec;text-align:center;"| | ||
| + | <math>P=P(r,\vartheta,\varphi)</math> | ||
| + | <math>0\leq r\leq\infty</math><br> | ||
| + | <math>0\leq \vartheta\leq\pi</math> | ||
| + | <math>0\leq \varphi < 2\pi</math><br> | ||
| + | |style="background-color:#dde6f3"|[[Image:Kugelkoordinaten.png|center|miniatur|Kugelkoordinaten]] | ||
| + | |} | ||
| + | |||
| + | <!-- | ||
| + | Namen der vorherigen Bilder aus dem Albach: | ||
| + | [[Image:Koordinatensysteme Das Kartesische Koordinatensystem.jpg|center|miniatur|Kartesische Koordinaten]] | ||
| − | + | [[Image:Koordinatensysteme Krummlinige Koordinaten3.jpg|center|miniatur|Zylinderkoordinaten]] | |
| − | |||
| − | |||
| − | + | [[Image:Koordinatensysteme Krummlinige Koordinaten4.jpg|center|miniatur|Kugelkoordinaten]] | |
| − | + | --> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Kategorie:Feedback]] | |
| + | [[Kategorie:Artikel]] | ||
Aktuelle Version vom 24. Oktober 2013, 16:28 Uhr
| ← Zurück: Formelsammlung zur Vektorrechnung | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Kartesische Koordinaten → |
Einführung
Koordinatensysteme werden zur eindeutigen Positionsbeschreibung von Punkten und Anordnungen (z. B. Ladungen oder stromführende Leiter) im Raum verwendet und ermöglichen erst die eindeutige Formulierung von Vektoren. Weiterhin lassen sich ortsabhängige Größen wie beispielsweise elektrische und magnetische Felder beschreiben. In der Lehrverstaltung sind neben den bekannten kartesischen Koordinaten besonders Zylinder- und Kugelkoordinaten von Bedeutung. Auch bei diesen beiden Koordinatensystemen dient das kartesische Koordinatensystem jedoch immer als Referenz. In der Regel ist es vorteilhaft, ein auf die jeweilige Problemstellung „zugeschnittenes“ Koordinatensystem zu verwenden. Das elektrische Feld einer Punktladung 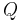 ist beispielsweise radialsymmetrisch und der Betrag hängt ausschließlich vom Abstand
ist beispielsweise radialsymmetrisch und der Betrag hängt ausschließlich vom Abstand 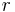 zur Punktladung ab, so dass sich die Verwendung von Kugelkoordinaten anbietet. Mit Hilfe eines entsprechenden Einheitsvektors lässt sich die elektrische Feldstärke wie folgt angeben:
zur Punktladung ab, so dass sich die Verwendung von Kugelkoordinaten anbietet. Mit Hilfe eines entsprechenden Einheitsvektors lässt sich die elektrische Feldstärke wie folgt angeben:
Die äquivalente Beschreibung in kartesischen Koordinaten ist weniger kompakt und lautet wie folgt (vgl. Formelsammlung Koordinatensysteme):
Mit Hilfe von trigonometrischen Funktionen können auch die aus dem Kugelkoordinatensystem stammenden Winkel  und
und 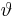 ersetzt werden, so dass die Gleichung nur noch von
ersetzt werden, so dass die Gleichung nur noch von  ,
, 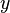 und
und 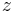 abhängt. Dadurch wird der Ausdruck noch umfangreicher. Eine „geschickte“ Wahl des Koordinatensystems kann außerdem zu erheblichen Vereinfachungen führen, beispielsweise bei der Bestimmung von Feldgrößen auf Basis von Mehrfachintegralen. Diesbezüglich ist es oft vorteilhaft, wenn der Koordinatenursprung – sofern frei wählbar – passend zu den Symmetrieeigenschaften einer Anordnung positioniert wird.
abhängt. Dadurch wird der Ausdruck noch umfangreicher. Eine „geschickte“ Wahl des Koordinatensystems kann außerdem zu erheblichen Vereinfachungen führen, beispielsweise bei der Bestimmung von Feldgrößen auf Basis von Mehrfachintegralen. Diesbezüglich ist es oft vorteilhaft, wenn der Koordinatenursprung – sofern frei wählbar – passend zu den Symmetrieeigenschaften einer Anordnung positioniert wird.
Bei den vorgestellten Koordinatensystemen handelt es sich um orthogonale Koordinatensysteme. Dabei stehen die in Richtung wachsender Koordinatenwerte zeigenden Einheitsvektoren senkrecht aufeinander. Werden diese allgemein mit 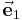 ,
, 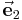 und
und 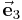 bezeichnet, so folgt mit dem Skalarprodukt:
bezeichnet, so folgt mit dem Skalarprodukt:
Da die Koordinatenlinien bei den Zylinder- und Kugelkoordinaten nicht geradlinig verlaufen, werden diese als krummlinige orthogonale Koordinatensysteme bezeichnet. Bei dem kartesischen Koordinatensystem handelt es sich also um ein geradliniges orthogonales Koordinatensystem. Darüber hinaus handelt es sich um Rechtssysteme (prinzipiell sind auch andere Konventionen möglich), so dass das Vektorprodukt von zwei aufeinander folgenden Einheitsvektoren den jeweils nächsten Einheitsvektor liefert:
Die nachfolgende Tabelle zeigt eine Übersicht der verschiedenen Koordinatensysteme.
Übersicht
| Kartesische Koordinaten
Bei dem kartesischen Koordinatensystem wird ein Punkt |
|
|
| Zylinderkoordinaten
Bei den Zylinderkoordinaten wird ein Punkt |
|
|
| Kugelkoordinaten
Bei dem Kugelkoordinatensystem wird ein Punkt |
|
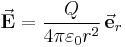
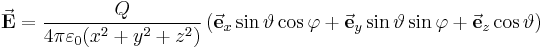
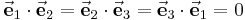
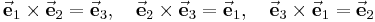
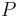 im Raum durch die drei Koordinaten
im Raum durch die drei Koordinaten 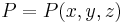
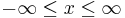

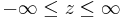
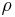 ,
, 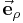 und
und 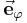 hängt von der Position des betrachteten Punktes ab. Betrachtet man ausschließlich die
hängt von der Position des betrachteten Punktes ab. Betrachtet man ausschließlich die 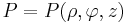
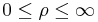
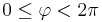
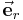 ,
, 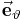 und
und