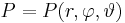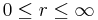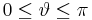Orthogonale Koordinatensysteme:Übersicht: Unterschied zwischen den Versionen
| Zeile 46: | Zeile 46: | ||
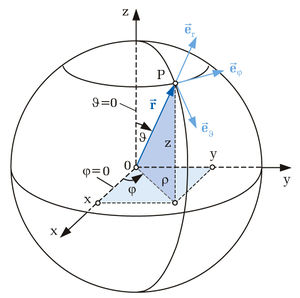
Bei dem Kugelkoordinatensystem bestimmt ''r'' den Abstand zum Ursprung. <math>\varphi</math> wird wie bei den Zylinderkoordinaten zwischen der positiven x-Achse und dem Punkt P angegeben und verläuft dabei entgegen des Uhrzeigersinns. Dabei entsprechen Punkte mit dem selben <math>\varphi</math>-Wert Punkten mit dem selben "Längengrad". Die dritte Koordinate ist der Winkel <math>\vartheta</math>, er wird zwischen der positiven z-Achse und dem Punkt P gemessen. Auch hier gilt, alle Punkte mit dem selben Winkel <math>\vartheta</math> liegen auf dem selben "Breitengrad". | Bei dem Kugelkoordinatensystem bestimmt ''r'' den Abstand zum Ursprung. <math>\varphi</math> wird wie bei den Zylinderkoordinaten zwischen der positiven x-Achse und dem Punkt P angegeben und verläuft dabei entgegen des Uhrzeigersinns. Dabei entsprechen Punkte mit dem selben <math>\varphi</math>-Wert Punkten mit dem selben "Längengrad". Die dritte Koordinate ist der Winkel <math>\vartheta</math>, er wird zwischen der positiven z-Achse und dem Punkt P gemessen. Auch hier gilt, alle Punkte mit dem selben Winkel <math>\vartheta</math> liegen auf dem selben "Breitengrad". | ||
|style="background-color:#c9d7ec"| | |style="background-color:#c9d7ec"| | ||
| − | :<math>P(r,\varphi,\vartheta) | + | :<math>P=P(r,\varphi,\vartheta)</math> |
:<math>0\leq r\leq\infty</math> | :<math>0\leq r\leq\infty</math> | ||
:<math>0\leq \varphi\leq 2\pi</math> | :<math>0\leq \varphi\leq 2\pi</math> | ||
Version vom 29. Mai 2012, 10:28 Uhr
Einführung
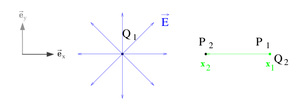
Bei vielen verschiedenen Anwendungen ist es nötig, die Position im Raum relativ zueinander zu kennen von was?. In der Elektrotechnik ist es beispielsweise sinnvoll, Koordinatensysteme zu wählen, um verschiedene Punktladungen im Raum darstellen zu können Formulierung. Ein Beispiel hierfür ist die Kraftwirkung der Punktladungen, die durch ihre relative Position zueinander im Raum berechnet wird Formulierung. Außerdem lassen sich durch die Koordinatensysteme viele Effekte am Modell veranschaulichen Verwirrend. Die Betrachtung von Äquipotentialflächen ist eine davon.
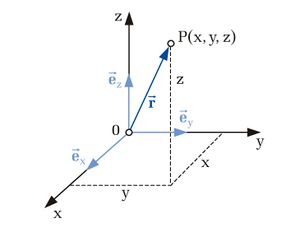
Die Positionen im Raum bestimmt man unter der Verwendung eines willkürlichen aber fest gewählten Bezugspunktes. So kann ein Punkt P durch einen Vektor beschrieben werden, der von einem Bezugspunkt (wird willkürlich zu 0 gesetzt doppelt) zu dem Punkt P zeigt. Der Vektor wird dann entweder mit Hilfe der Koordinatendarstellung oder der Komponentendarstellung beschrieben 2x Komponentendarstellung. Die Komponenten werden dabei in der Regel so gewählt, dass sie zueinander orthogonal sind, also senkrecht aufeinander stehen. Um den Punkten und Vektoren bestimmte Werte zuzuordnen, wählt man Koordinatensysteme, die den Raum vollständig beschreiben können unklar bzw. verwirrend.
Da unterschiedliche Problemstellungen unterschiedlich komplexe Darstellungen erfordern, gibt es auch verschiedene Koordinatensysteme. Vergleicht man beispielsweise die Strecke, die ein Auto auf einer Ebene zurücklegt mit der eines Flugzeugs, so zeigt sich, dass bei dem Auto eine zweidimensionale Betrachtung ausreicht, während das Flugzeug nicht vollständig dadurch beschrieben werden kann.
An dieser Stelle werden nur orthogonale Koordinatensysteme behandelt, da sie leicht nachvollziehbar und vorstellbar sind und für die in der Vorlesung gezeigten Probleme ausreichen. Bei den drei in den folgenden Abschnitten betrachteten Fällen, nämlich den kartesischen Koordinaten, den Zylinderkoordinaten und den Kugelkoordinaten, handelt es sich um solche orthogonale Koordinatensysteme. Außerdem sind es so genannte Rechtssysteme, deshalb weisen die Einheitsvektoren 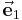 ,
, 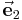 ,
, 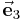 immer in die Richtung wachsender Koordinatenwerte und stehen dabei senkrecht aufeinander. Setzt man die Einheitsvektoren in das Skalarprodukt ein, ergibt sich durch die Orthogonalität automatisch:
immer in die Richtung wachsender Koordinatenwerte und stehen dabei senkrecht aufeinander. Setzt man die Einheitsvektoren in das Skalarprodukt ein, ergibt sich durch die Orthogonalität automatisch:
Ebenso gilt bei einem Rechtssystem, dass das Vektorprodukt zweier aufeinander folgender Einheitsvektoren den jeweils nächsten Einheitsvektor ergeben muss, dies kann auch durch die [Rechte Hand Regel1] veranschaulicht werden:
Übersicht
| Das kartesische Koordinatensystem
Bei dem kartesischen Koordinatensystem sind die Koordinatenachsen geradlinig und orthogonal angeordnet, so dass die Achsen ein Rechtssystem bilden, welches durch die Rechte Handregel1 beschrieben werden kann. Der Schnittpunkt der Achsen wird Koordinatenursprung genannt. Die Einheitsvektoren sind parallel zu den Achsen angeordnet und zeigen immer in Richtung wachsender Koordinatenwerte, daher sind die Einheitsvektoren auch unabhängig von der Position des Punktes im Raum und zeigen immer dieselbe Richtung an. |
|
|
| Zylinderkoordinaten
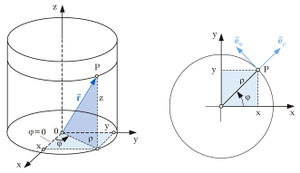
Bei den Zylinderkoordinaten bleibt die z-Koordinate im Vergleich zu den kartesischen Koordinaten unverändert. In der xy-Ebene werden allerdings die Koordinaten |
|
|
| Kugelkoordinaten
Bei dem Kugelkoordinatensystem bestimmt r den Abstand zum Ursprung. |
|
|
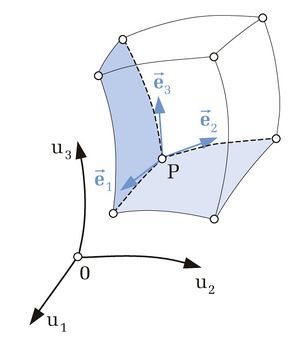
| Krummlinige orthogonale Koordinatensysteme |
|
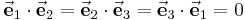
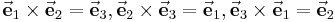
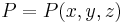
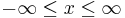

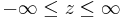
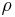 und
und  verwendet.
verwendet. 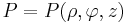
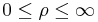
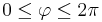
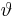 , er wird zwischen der positiven z-Achse und dem Punkt P gemessen. Auch hier gilt, alle Punkte mit dem selben Winkel
, er wird zwischen der positiven z-Achse und dem Punkt P gemessen. Auch hier gilt, alle Punkte mit dem selben Winkel