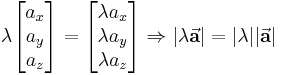Einfache Rechenoperationen mit Vektoren
| ← Zurück: Einheitsvektoren | Übersicht: Vektorrechnung | Vorwärts: Skalarprodukt → |
|
Zu diesem Thema stehen Aufgaben zur Selbstkontrolle zur Verfügung. |
Addition und Subtraktion von Vektoren
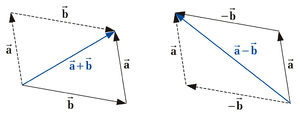
Vektoren lassen sich sowohl graphisch als auch rechnerisch addieren. Bei der grafischen Addition wird einer der Vektoren parallel verschoben, so dass sein Anfang an der Spitze des zweiten Pfeils liegt (die Vektoren werden also sozusagen aneinandergereiht). Der resultierende Vektor wird als Summenvektor bezeichnet und zeigt vom Anfangspunkt des einen Vektors zur Spitze des parallel verschobenen Vektors (siehe Abbildung). Zur mathematischen Bestimmung des Summenvektors werden die einzelnen Komponenten addiert:
Sowohl anhand der grafischen Addition — es spielt offensichtlich keine Rolle welcher der beiden Vektoren an die Spitze des anderen verschoben wird — als auch anhand der rechnerischen Bestimmung des Summenvektors wird deutlich, dass die Vektoraddition dem Kommutativgesetz genügt. Folglich gilt:
Bei der Subtraktion zweier Vektoren wird der resultierende Vektor als Differenzvektor bezeichnet. Zur graphischen Bestimmung des Differenzvektors 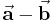 lässt sich ausnutzen, dass
lässt sich ausnutzen, dass 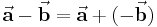 gilt. Dies bedeutet nämlich, dass die beiden Vektoren einfach addiert werden können, sofern man zuvor die Richtung des Vektors
gilt. Dies bedeutet nämlich, dass die beiden Vektoren einfach addiert werden können, sofern man zuvor die Richtung des Vektors  umkehrt. Zur mathematischen Bestimmung des Differenzvektors werden die einzelnen Komponenten subtrahiert:
umkehrt. Zur mathematischen Bestimmung des Differenzvektors werden die einzelnen Komponenten subtrahiert:
Zur Addition und Subtraktion von mehr als zwei Vektoren gelten die beschriebenen Beziehungen in analoger Weise, bei der graphischen Addition werden also beispielsweise sämtliche Vektoren aneinandergereiht.
Ein häufiger Anwendungsfall der Vektoraddition ergibt sich bei der Bestimmung von resultierenden Feldgrößen im Raum, da diese meist durch Überlagerung mehrerer einzelner Felder bestimmt werden können. Betrachtet man beispielsweise zwei Punktladungen Die Vektoren der elektrischen Feldstärke, die von der positiven Ladung Fasst man die Summenvektoren als gerichtete Tangenten auf, so beschreiben die zugehörigen Kurven die korrespondierenden Feldlinien. |
Multiplikation von Vektoren mit einem Skalar
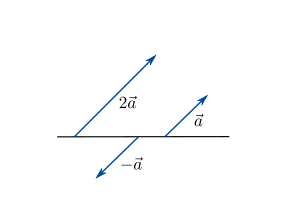
Bei der Multiplikation eines Vektors  mit einem positiven reellen Skalar
mit einem positiven reellen Skalar 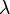 erhält man einen neuen Vektor, dessen Richtung mit derjenigen des ursprünglichen Vektors übereinstimmt. Bei der Multiplikation eines Vektors
erhält man einen neuen Vektor, dessen Richtung mit derjenigen des ursprünglichen Vektors übereinstimmt. Bei der Multiplikation eines Vektors  mit einem negativen reellen Skalar
mit einem negativen reellen Skalar 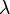 erhält man einen Vektor mit entgegengesetzter Richtung. Die Länge des neuen Vektors ändert sich in beiden Fällen um den Faktor
erhält man einen Vektor mit entgegengesetzter Richtung. Die Länge des neuen Vektors ändert sich in beiden Fällen um den Faktor 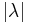 . Dies wird sofort anhand der mathematischen Bestimmung des neuen Vektors ersichtlich, bei der jede Komponente des Vektors mit dem Skalar multipliziert wird:
. Dies wird sofort anhand der mathematischen Bestimmung des neuen Vektors ersichtlich, bei der jede Komponente des Vektors mit dem Skalar multipliziert wird:
Bei der Multiplikation mit einem Skalar 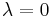 erhält man als Sonderfall den Nullvektor
erhält man als Sonderfall den Nullvektor 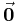 mit dem Betrag
mit dem Betrag 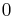 und unbestimmter Richtung. Ein praktisches Beispiel für die Multiplikation eines Vektors mit einem Skalar findet sich in der Einführung in die Vektorrechnung.
und unbestimmter Richtung. Ein praktisches Beispiel für die Multiplikation eines Vektors mit einem Skalar findet sich in der Einführung in die Vektorrechnung.
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/VectorsIn3D/ Applet: Vektoraddition im dreidimensionalem Raum (engl.) http://demonstrations.wolfram.com/3DVectorDecomposition/ Applet: Vektoraddition im dreidimensionalem Raum mit 3 Vektoren (engl.) http://demonstrations.wolfram.com/SumOfTwoVectors/ Applet: Vektoraddition in kartesischen Koordinaten (engl.) |
Hilfreiche Links
|
http://hyperphysics.phy-astr.gsu.edu/hbase/vect.html Allgemeine Einführung in Vektoroperationen (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Anthony Croft und Robert Davison, Mathematics for Engineers: a modern interactive approach, 3. Auflage (Pearson-Prentice Hall, 2008)
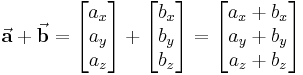
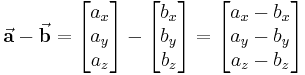
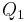 und
und 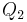 , so rufen beide Ladungen unabhängig voneinander die elektrischen Feldstärken
, so rufen beide Ladungen unabhängig voneinander die elektrischen Feldstärken 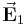 und
und 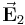 hervor (siehe Abbildung).
hervor (siehe Abbildung).
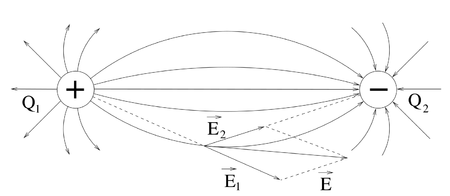
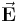 in jedem Punkt im Raum lässt sich nun dadurch bestimmen, dass die dort vorliegenden Einzelfeldstärken vektoriell addiert werden:
in jedem Punkt im Raum lässt sich nun dadurch bestimmen, dass die dort vorliegenden Einzelfeldstärken vektoriell addiert werden:
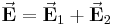
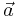 mit einem Skalar
mit einem Skalar