Adjugate Formula
| ← Back: Gauß-Jordan-Algorithm | Overview: Matrix inversion | Next: Vector algebra → |
The adjugate formula defines the inverse of an n-by-n square matrix 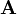 as
as
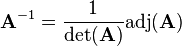
where 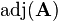 is the so called adjugate matrix of
is the so called adjugate matrix of 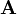 . The adjugate matrix is the transposed of the cofactor matrix:
. The adjugate matrix is the transposed of the cofactor matrix:
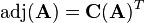
And the cofactor matrix 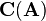 is just a matrix where each cell corresponds to the related cofactor:
is just a matrix where each cell corresponds to the related cofactor:
![\mathbf{C}(\mathbf{A})=\left[\begin{array}{cccc}
C_{1,1}(\mathbf{A}) & C_{1,2}(\mathbf{A}) & \cdots & C_{1,n}(\mathbf{A})\\
C_{2,1}(\mathbf{A}) & C_{2,2}(\mathbf{A}) & & C_{2,n}(\mathbf{A})\\
\vdots & & \ddots & \vdots\\
C_{n,1}(\mathbf{A}) & C_{n,2}(\mathbf{A}) & \cdots & C_{n,n}(\mathbf{A})
\end{array}\right]](/wiki/robotics/images/math/c/b/7/cb7505ec4a107c95fd31601fac888472.png)
So to determine the inverse of an n-by-n square matrix you have to compute the n square cofactors, then transpose the resulting cofactor matrix and divide all the values by the determinant.
|
![\mathbf{A}_e =
\left[\begin{array}{cccc}
1 & 2 & 0 & 0\\
3 & 0 & 1 & 1\\
0 & 1 & 0 & 0\\
0 & 0 & 2 & 1
\end{array}\right]](/wiki/robotics/images/math/a/3/8/a386cb4eac26aca26ac89fd336061a0e.png)
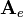 has already been described in the example for
has already been described in the example for ![\mathbf{C}(\mathbf{A}_e)=
\left[\begin{array}{cccc}
1 & 0 & 3 & -6\\
0 & 0 & -1 & 2\\
-2 & 1 & -6 & 12\\
0 & 0 & 1 & -1
\end{array}\right]](/wiki/robotics/images/math/2/c/1/2c171afbf8b3bb79274d1b6d160574ad.png)
![\mathbf{C}(\mathbf{A}_e)^T=
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]=\text{adj}(\mathbf{A}_e)](/wiki/robotics/images/math/4/d/6/4d60f99b73fcd16a1e7f14e381e93148.png)
![\mathbf{A}_e^{-1}=\frac{1}{\det(\mathbf{A}_e)}\text{adj}(\mathbf{A}_e)
=\frac{1}{1}
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]
=
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]](/wiki/robotics/images/math/1/f/3/1f3b7de9ef6df9ca9270bf2b7d321cb6.png)