Homogeneous coordinates
| ← Back: Rotation | Overview: Transformations | Next: Combinations of transformations → |
Rotation of n-dimensional coordinates can be described by an n-by-n matrix. All the components of the matrix are multiplied with one of the 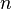 coordinates. So the transformation is dependent on the original coordinates. Translation however is actually a vector addition and so independent of the original coordinates (see subarticle about translation).
coordinates. So the transformation is dependent on the original coordinates. Translation however is actually a vector addition and so independent of the original coordinates (see subarticle about translation).
To be able to also apply a translation by matrix multiplication, an additional dimension is introduced. For three-dimensional space (which is usually regarded in robotics), the homogeneous transformation matrix  is a 4-by-4 matrix.
is a 4-by-4 matrix.  consists of the 3-by-3 rotation matrix
consists of the 3-by-3 rotation matrix  and a 3-by-1 translation vector
and a 3-by-1 translation vector 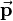 combined with the last row of the identity matrix:
combined with the last row of the identity matrix:
Let the components of the rotation matrix be denoted as follows:
to the standard transformation matrix matrix, where the top left n-by-n submatrix The additional component of vectors is always a 1. So the multiplication for 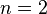 for example results in:
for example results in:
As can be seen in the resulting vector, the components 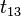 and
and 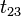 are independent of the original coordinates and just added to the x- or the y-coordinate, respectively.
are independent of the original coordinates and just added to the x- or the y-coordinate, respectively.
![\mathbf{T}=
\left[\begin{array}{ccc|c}
& & & \\
& \mathbf{R} & & \vec{\mathbf{p}}\\
& & & \\ \hline
0 & 0 & 0 & 1
\end{array}\right]=
\left[\begin{array}{ccc|c}
& & & \\
\vec{\mathbf{x}} & \vec{\mathbf{y}} & \vec{\mathbf{z}} & \vec{\mathbf{p}}\\
& & & \\ \hline
0 & 0 & 0 & 1
\end{array}\right]=
\left[\begin{array}{ccc|c}
& & & \mathbf{p}_x\\
\vec{\mathbf{x}} & \vec{\mathbf{y}} & \vec{\mathbf{z}} & \mathbf{p}_y\\
& & & \mathbf{p}_z\\ \hline
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/2/9/c/29cf5f918245624ab6c08a36279410cc.png)
![\left[\begin{array}{c}
x_1\\
y_1\\
1
\end{array}\right]=
\mathbf{T} \cdot
\left[\begin{array}{c}
x_0\\
y_0\\
1
\end{array}\right]=
\left[\begin{array}{ccc}
t_{11} & t_{12} & t_{13}\\
t_{21} & t_{22} & t_{23}\\
0 & 0 & 1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0\\
y_0\\
1
\end{array}\right]=
\left[\begin{array}{c}
t_{11}\cdot x_0+t_{12}\cdot y_0+t_{13}\cdot 1\\
t_{21}\cdot x_0+t_{22}\cdot y_0+t_{23}\cdot 1\\
0\cdot x_0+0\cdot y_0+1\cdot1
\end{array}\right]=
\left[\begin{array}{c}
t_{11}\cdot x_0+t_{12}\cdot y_0+{\color{Green}\mathbf{t_{13}}}\\
t_{21}\cdot x_0+t_{22}\cdot y_0+{\color{Green}\mathbf{t_{23}}}\\
1
\end{array}\right]](/wiki/robotics/images/math/8/0/6/8061998f64ac8d490e4583a8d672fe22.png)