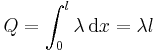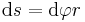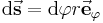Wegelemente: Unterschied zwischen den Versionen
| Zeile 21: | Zeile 21: | ||
\mathrm{d}s = \mathrm{d}\varphi r | \mathrm{d}s = \mathrm{d}\varphi r | ||
</math> | </math> | ||
| − | Mit Hilfe der [[Zylinderkoordinaten|Polarkoordinaten]] ist auch die Angabe gerichteter Elemente möglich, | + | Mit Hilfe der [[Zylinderkoordinaten|Polarkoordinaten]] ist auch die Angabe gerichteter Elemente möglich, bei einer Orientierung entgegen des Uhrzeigersinns ergibt sich hier zum Beispiel das folgende Element: |
:<math> | :<math> | ||
\mathrm{d}\vec{\textbf{s}} = \mathrm{d}\varphi r \vec{\textbf{e}}_\varphi | \mathrm{d}\vec{\textbf{s}} = \mathrm{d}\varphi r \vec{\textbf{e}}_\varphi | ||
Version vom 29. August 2012, 21:04 Uhr
Neu
Infinitesimale Wegelemente sind beliebig kleine Teilelemente einer Kontur, die meist mit 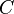 bezeichnet wird. Sie werden zum Beispiel im Zusammenhang mit Linienintegralen benötigt. Die Elemente werden meist mit
bezeichnet wird. Sie werden zum Beispiel im Zusammenhang mit Linienintegralen benötigt. Die Elemente werden meist mit 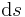 beziehungsweise bei einer gerichteten Kontur mit
beziehungsweise bei einer gerichteten Kontur mit 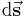 bezeichnet. Da es sich um beliebig kleine Teilelemente einer Kontur handelt, ist eine eventuell vorhandene Krümmung eines einzelnen Teilelements vernachlässigbar. Die Richtung in einem bestimmten Punkt der Kontur entspricht dabei derjenigen einer in diesem Punkt angelegten Tangente.
bezeichnet. Da es sich um beliebig kleine Teilelemente einer Kontur handelt, ist eine eventuell vorhandene Krümmung eines einzelnen Teilelements vernachlässigbar. Die Richtung in einem bestimmten Punkt der Kontur entspricht dabei derjenigen einer in diesem Punkt angelegten Tangente.
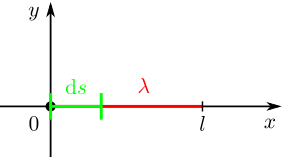
Am häufigsten werden geradlinige oder kreisförmige Konturen (bzw. Teile davon, d. h. Kreisbögen) verwendet. Ist beispielsweise eine auf der  -Achse gelegene und konstante Linienladungsdichte (=Ladungsmenge/Strecke)
-Achse gelegene und konstante Linienladungsdichte (=Ladungsmenge/Strecke) 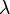 gegeben (siehe Abbildung), so erhält man die Gesamtladung
gegeben (siehe Abbildung), so erhält man die Gesamtladung 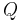 durch Integration über diese Strecke.
durch Integration über diese Strecke.
Ein beliebig kleines Teilstück der  -Achse ist dann durch
-Achse ist dann durch 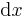 gegeben, so dass das zugehörige Integral folgende Form annimmt:
gegeben, so dass das zugehörige Integral folgende Form annimmt:
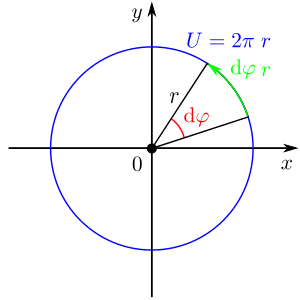
Bei einer kreisförmigen Kontur, wie sie in der nachfolgenden Abbildung dargestellt ist, bietet sich die Verwendung von Polarkoordinaten an.
Ein beliebig kleines Teilstück der Kreiskontur schließt dabei einen ebenfalls beliebig kleinen Winkel 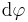 ein. Der Gesamtumfang des Kreises ergibt sich gemäß
ein. Der Gesamtumfang des Kreises ergibt sich gemäß 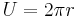 . Hierbei entspricht der Wert
. Hierbei entspricht der Wert 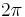 dem vom Kreis erfassen Winkel im Bogenmaß. Hat man nun also nur noch ein beliebig kleines Teilstück des Kreises und damit statt
dem vom Kreis erfassen Winkel im Bogenmaß. Hat man nun also nur noch ein beliebig kleines Teilstück des Kreises und damit statt 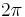 nur noch einen Winkel
nur noch einen Winkel 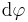 gegeben, so folgt für das entsprechende Wegelement:
gegeben, so folgt für das entsprechende Wegelement:
Mit Hilfe der Polarkoordinaten ist auch die Angabe gerichteter Elemente möglich, bei einer Orientierung entgegen des Uhrzeigersinns ergibt sich hier zum Beispiel das folgende Element:
Alt
Betrachtet man in der Abbildung das Wegelement 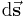 , so fällt auf, dass es in beliebige Richtungen zeigt (hä? woran soll das hier auffallen?), ebenso wie auch die Kontur im Durchflutungssatz eine beliebige (nein, sie muss zumindest geschlossen sein, also isrt sie nicht beliebig) Form annehmen kann. Wichtig ist hierbei, dass das Wegelement
, so fällt auf, dass es in beliebige Richtungen zeigt (hä? woran soll das hier auffallen?), ebenso wie auch die Kontur im Durchflutungssatz eine beliebige (nein, sie muss zumindest geschlossen sein, also isrt sie nicht beliebig) Form annehmen kann. Wichtig ist hierbei, dass das Wegelement 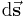 als infinitesimales Wegstück aufgefasst werden soll. Es ist also ein sehr kleines Wegstück, so klein, dass die Krümmung des einzelnen Wegstücks vernachlässigbar wird.
als infinitesimales Wegstück aufgefasst werden soll. Es ist also ein sehr kleines Wegstück, so klein, dass die Krümmung des einzelnen Wegstücks vernachlässigbar wird.
In den nebenstehenden Abbildungen (nebenstehend sind keine Abbildungen) sind zwei beispielhafte Verläufe einer Linienladung dargestellt. Im ersten Fall verläuft die Linienladung nur entlang der x-Achse. Das Wegelement kann hier also mit dem Differential 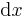 dargestellt (wirklich dargestellt?) werden, da die zu integrierenden Funktion
dargestellt (wirklich dargestellt?) werden, da die zu integrierenden Funktion 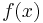 nur von x abhängt.
nur von x abhängt.
Ist jedoch der Kurvenverlauf aus der zweiten Abbildung gegeben, ist die Funktion von x und y abhängig 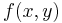 . Nun kann man nicht einfach nach
. Nun kann man nicht einfach nach 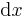 und
und 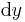 integrieren, weil so eine Fläche aufgespannt wird und man so ein Flächenelement
integrieren, weil so eine Fläche aufgespannt wird und man so ein Flächenelement 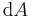 erhält (Argumentation des letzten Satzes unschlüssig). Da hier ein Kreisbogen betrachtet wird, bietet sich die Verwendung von Polarkoordinaten, da so der Kreisbogen nur noch von einer Koordinate
erhält (Argumentation des letzten Satzes unschlüssig). Da hier ein Kreisbogen betrachtet wird, bietet sich die Verwendung von Polarkoordinaten, da so der Kreisbogen nur noch von einer Koordinate  abhängt (1. Du sprechen Deutsch? 2. "Der Kreisbogen" ist doch Quatsch. Ist die LÄNGE DES KREISBOGENS gemeint?).
abhängt (1. Du sprechen Deutsch? 2. "Der Kreisbogen" ist doch Quatsch. Ist die LÄNGE DES KREISBOGENS gemeint?).
Es muss darauf geachtet werden, dass vor allem bei den gekrümmten orthogonalen Koordinaten oft Korrekturfaktoren (Man weiß doch gar nicht, was Korrekturfaktoren sein sollen!) bei infinitesimalen Elementen zu berücksichtigen sind. Hier ist die Koordinate  auch vom Radius r abhängig. Dies entspricht einer Umfangsberechnung des Kreises. Der Kreis hat einen Gesamtumfang von
auch vom Radius r abhängig. Dies entspricht einer Umfangsberechnung des Kreises. Der Kreis hat einen Gesamtumfang von 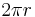 . Betrachtet man ein kleines Teilstück des Kreises folgt:
. Betrachtet man ein kleines Teilstück des Kreises folgt: 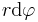 (In Grafik untereinander darstellen).
(In Grafik untereinander darstellen).
In dieser Vorlesung werden nur einfache Verläufe entlang der Koordinatenachsen uns bekannter Koordinatensysteme verwendet (stimmt nicht!!!). Für kompliziertere Verläufe gibt es (besser: existieren) mathematische Hilfsmittel, auf die hier aber nicht näher eingegangen werden soll (wird!). Es werden hauptsächlich für Wegelemente in den kartesischen Koordinaten 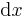 ,
,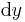 oder
oder 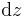 , in den Zylinderkoordinaten
, in den Zylinderkoordinaten 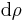 oder
oder 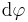 und in den Kugelkoordinaten
und in den Kugelkoordinaten 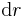 verwendet (Du sprechen Deutsch?).
verwendet (Du sprechen Deutsch?).
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Klaus Jänich Mathematik 1 Geschrieben für Physiker,2. Auflage (Springer Berlin Heidelberg, 2005)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Hempel, "Mathematische Grundlagen", Linienintegral, Universität Magdeburg
| ← Zurück: Infinitesimale Weg-, Flächen-, und Volumenelemente | Übersicht: Infinitesimale Weg-, Flächen-, und Volumenelemente | Vorwärts: Flächenelemente → |