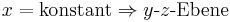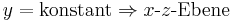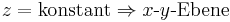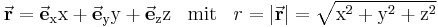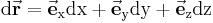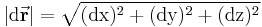Kartesische Koordinaten: Unterschied zwischen den Versionen

Aus GET A
Wechseln zu: Navigation, Suche
Zeile 51: Zeile 51:
 
</math>
 
</math>
  
−
Die Umrechnung der Koordinaten und Einheitsvektoren zwischen den verschiedenen Koordinatensystemen sind in der [[Formelsammlung Koordinatensysteme]] angegeben. Das kartesische Koordinatensystem wird immer auch als Referenz (Bezug) bei der Verwendung von [[Zylinderkoordinaten|Zylinder-]] und [[Kugelkoordinaten]] verwendet. So wird beispielsweise der Winkel <math>\varphi</math> in Zylinderkoordinaten ausgehend von der positiven <math>x</math>-Achse in Richtung der positiven <math>y</math>-Achse gezählt.
+
Die Koordinaten und Einheitsvektoren zwischen der verschiedenen Koordinatensystemen können ineinander umgerechnet werden, siehe hierzu [[Formelsammlung Koordinatensysteme]]. Das kartesische Koordinatensystem wird immer auch als Referenz (Bezug) bei der Verwendung von [[Zylinderkoordinaten|Zylinder-]] und [[Kugelkoordinaten]] verwendet. So wird beispielsweise der Winkel <math>\varphi</math> in Zylinderkoordinaten ausgehend von der positiven <math>x</math>-Achse in Richtung der positiven <math>y</math>-Achse gezählt.
  
  

Version vom 28. August 2012, 21:39 Uhr

To-do:

  • Formulierungen überarbeiten
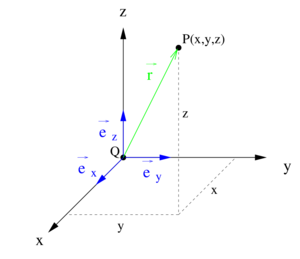
Das Kartesische Koordinatensystem
Vektorielles Wegelement

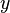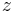Das kartesische Koordinatensystem ist das bekannteste Koordinatensystem. Dabei werden die geradlinig und orthogonal (rechtwinklig) zueinander verlaufenden Koordinatenachsen als x-, y- und z-Achse bezeichnet. Den Schnittpunkt dieser Achsen nennt man Koordinatenursprung oder kurz Ursprung. Die Einheitsvektoren 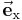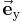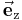\vec{\textbf{e}}_\mathrm{x}, \vec{\textbf{e}}_\mathrm{y}, \vec{\textbf{e}}_\mathrm{z} verlaufen jeweils parallel zu den zugehörigen Achsen und zeigen in Richtung wachsender Koordinatenwerte. Im Gegensatz zu Zylinder- und Kugelkoordinaten (dabei handelt es sich um krummlinige orthogonale Koordinatensysteme) zeigen die Einheitsvektoren unabhängig vom betrachteten Punkt im Raum immer in dieselbe Richtung.

Eine wichtige Eigenschaft des kartesischen Koordinatensystems besteht darin, dass die Einheitsvektoren ein Rechtssystem bilden, also gemäß der Rechten-Hand-Regel-II miteinander verknüpft sind. Dies trifft auch auf Zylinder- und Kugelkoordinaten zu.

Das kartesische Koordinatensystem wird nicht nur zur Beschreibung von Punkten oder Objekten im Raum, sondern auch zur Darstellung von Funktionsverläufen verwendet. So kann zum Beispiel der zeitliche Verlauf einer Spannung dadurch dargestellt werden, dass diese auf der Ordinate (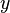y-Achse) und die zugehörige Zeit auf der Abszisse (x-Achse) angegeben wird. Hält man jeweils eine Koordinate konstant und lässt die anderen beiden beliebige Werte annehmen, so erhält man die orthogonal zueinander angeordneten Ebenen der jeweils verbleibenden Koordinatenachsen:

x = \text{konstant} \Rightarrow y\text{-}z\text{-Ebene}
y = \text{konstant} \Rightarrow x\text{-}z\text{-Ebene}
z = \text{konstant} \Rightarrow x\text{-}y\text{-Ebene}

Zur Beschreibung eines Punktes 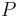P im Raum kann ein Ortsvektor 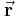\vec{\textbf{r}} verwendeten werden, der die Position des Punktes in Bezug zum Koordinatenursprung angibt (siehe Abbildung). Der Ortsvektor hat die Länge 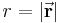r = \left| \vec{\textbf{r}} \right| und wird wie folgt beschrieben:

\begin{align} \vec{\textbf{r}} & = \vec{\textbf{e}}_\mathrm{x} \mathrm{x} + \vec{\textbf{e}}_\mathrm{y} \mathrm{y} + \vec{\textbf{e}}_\mathrm{z} \mathrm{z} && \text{mit} & r = \left| \vec{\textbf{r}} \right| = \sqrt{\mathrm{x}^2 + \mathrm{y}^2 + \mathrm{z}^2} \end{align}

Für die meisten Kurvenintegrale wird das differentielle Wegelement 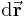\mathrm{d}\vec{\textbf{r}} benötigt. Dabei ist das differentielle Wegelement, die differentielle Änderung des Ortsvektors beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz. Dadurch wird die Richtung der Kurve in einem bestimmten Punkt angegeben.

\mathrm{d} \vec{\textbf{r}} = \vec{\textbf{e}}_\mathrm{x} \mathrm{dx} + \vec{\textbf{e}}_\mathrm{y} \mathrm{dy} + \vec{\textbf{e}}_\mathrm{z} \mathrm{dz}

Die Länge des Wegelements ergibt sich durch die Berechnung des Betrags des differentiellen Wegelements:

\left| \mathrm{d} \vec{\textbf{r}} \right| = \sqrt{(\mathrm{dx})^2 + (\mathrm{dy})^2 + (\mathrm{dz})^2}

Die Koordinaten und Einheitsvektoren zwischen der verschiedenen Koordinatensystemen können ineinander umgerechnet werden, siehe hierzu Formelsammlung Koordinatensysteme. Das kartesische Koordinatensystem wird immer auch als Referenz (Bezug) bei der Verwendung von Zylinder- und Kugelkoordinaten verwendet. 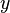So wird beispielsweise der Winkel \varphi in Zylinderkoordinaten ausgehend von der positiven x-Achse in Richtung der positiven y-Achse gezählt.


Multimediale Lehrmaterialien

Multimedia.png

http://www.mathe-online.at/mathint/zeich/applet_b_kartes.html Applet: Kartesische Koordinaten im zweidimensionalem Raum

http://www.mathe-online.at/mathint/zeich/applet_b_schief.html Applet: Schiefwinkliges Koordinatensystem im zweidimensionalem Raum

http://www.kleemannschule.de/de/unterricht/mathematik/punkt3D.html Applet: Ein Punkt im dreidimensionalem Raum mit seinen Ortsvektoren

Hilfreiche Links

Link.png

http://cnx.org/content/m13600/latest/ Übersicht zu verschiedenen Koordinatensystemen


← Zurück: Orthogonale Koordinatensysteme:Übersicht Übersicht: Orthogonale Koordinatensysteme Vorwärts: Zylinderkoordinaten →
Abgerufen von „https://getwww.uni-paderborn.de/wiki/geta/index.php?title=Kartesische_Koordinaten&oldid=4489“