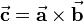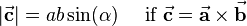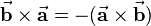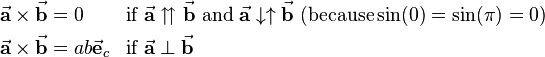Difference between revisions of "Cross product"
| (19 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{Navigation|before=[[Dot product]]|overview=[[Vector algebra]]|next=[[Matrices]]}} | {{Navigation|before=[[Dot product]]|overview=[[Vector algebra]]|next=[[Matrices]]}} | ||
| − | + | <table style="width:100%"><td style="width:50%">{{Exercise|Selftest: Cross product}}</td><td style="width:50%">{{Matlab|MATLAB: Cross product}}</td></table> | |
| − | |||
| − | + | [[File:vectoralgebra_crossproduct.jpg|right|350px]] | |
| + | |||
| + | The cross product of two vectors is denoted with an <math>\times</math>. The cross product of vector <math>\vec{\mathbf{a}}</math> and vector <math>\vec{\mathbf{b}}</math> results in a new vector | ||
| + | :<math>\vec{\mathbf{c}} = \vec{\mathbf{a}} \times \vec{\mathbf{b}}</math> | ||
| + | |||
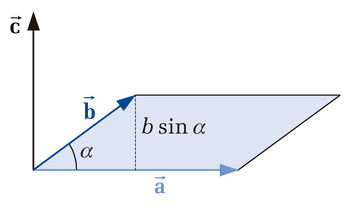
| + | that is perpendicular to the surface spanned by vectors <math>\vec{\mathbf{a}}</math> and <math>\vec{\mathbf{b}}</math> (see figure). Furthermore the three vectors <math>\vec{\mathbf{a}}</math>, <math>\vec{\mathbf{b}}</math> and <math>\vec{\mathbf{c}}</math> build a rectangular coordinate system based on the right-hand rule. The magnitude of vector <math>\vec{\mathbf{c}}</math> equals the area of the parallelogram spanned by <math>\vec{\mathbf{a}}</math> and <math>\vec{\mathbf{b}}</math> and is calculated as follows: | ||
:<math> | :<math> | ||
| − | |\vec{\ | + | |\vec{\mathbf{c}}| = a b \sin(\alpha)\ \quad\text{if}\ \vec{\mathbf{c}} = \vec{\mathbf{a}} \times \vec{\mathbf{b}} |
</math> | </math> | ||
| − | + | ||
| + | In this equation <math>\alpha</math> denotes the angle between the two vectors which ranges from <math>0</math> to <math>\pi</math> (see figure above). Furthermore it should be noted that the cross product is exclusively defined for the three-dimensional euclidian vector space. Therefore the following computational relationship holds: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 14: | Line 19: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | + | ||
| + | Based on the described relationships it can be seen, that the commutative law does not hold for the cross product. Instead, the following holds: | ||
:<math> | :<math> | ||
| − | + | \vec{\mathbf{b}} \times \vec{\mathbf{a}} = -(\vec{\mathbf{a}} \times \vec{\mathbf{b}}) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \vec{\ | ||
</math> | </math> | ||
| − | + | Furthermore there are some special cases that lead to simplifications in technical context: | |
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| − | \vec{\textbf{a}}\times\vec{\ | + | \vec{\textbf{a}}\times\vec{\mathbf{b}} &= 0 &\text{if}&\ \vec{\textbf{a}} \upuparrows \vec{\textbf{b}}\ \text{and}\ \vec{\textbf{a}} \downarrow\uparrow \vec{\textbf{b}}\ (\text{because} \sin(0) = \sin(\pi) = 0)\\ |
| − | \vec{\textbf{a}}\times\vec{\ | + | \vec{\textbf{a}}\times\vec{\mathbf{b}} &= a b \vec{\textbf{e}}_c &\text{if}&\ \vec{\textbf{a}} \perp \vec{\textbf{b}} |
\end{align} | \end{align} | ||
| − | </math><br/ | + | </math><br/><br/> |
{{Multimedia|Links= | {{Multimedia|Links= | ||
| − | |||
| − | |||
http://demonstrations.wolfram.com/CrossProductOfVectorsInTheYZPlane/ '''Applet''': Cross product of two vectors in the yz-plane | http://demonstrations.wolfram.com/CrossProductOfVectorsInTheYZPlane/ '''Applet''': Cross product of two vectors in the yz-plane | ||
}} | }} | ||
| − | <noinclude>== | + | <noinclude>==Literature== |
* Manfred Albach, ''Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen'', 3. Edition (Pearson Studium, 2011) | * Manfred Albach, ''Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen'', 3. Edition (Pearson Studium, 2011) | ||
* Kurt Meyberg und Peter Vachenauer, ''Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung'', 6. Edition (Springer Berlin Heidelberg, 2001) | * Kurt Meyberg und Peter Vachenauer, ''Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung'', 6. Edition (Springer Berlin Heidelberg, 2001) | ||
| Line 48: | Line 43: | ||
[[Category:Article]] | [[Category:Article]] | ||
| + | [[Category:Vectors]] | ||
Latest revision as of 17:37, 24 November 2017
| ← Back: Dot product | Overview: Vector algebra | Next: Matrices → |
|
|
The cross product of two vectors is denoted with an 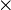 . The cross product of vector
. The cross product of vector 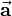 and vector
and vector 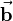 results in a new vector
results in a new vector
that is perpendicular to the surface spanned by vectors 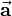 and
and 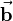 (see figure). Furthermore the three vectors
(see figure). Furthermore the three vectors 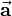 ,
, 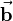 and
and 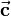 build a rectangular coordinate system based on the right-hand rule. The magnitude of vector
build a rectangular coordinate system based on the right-hand rule. The magnitude of vector 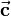 equals the area of the parallelogram spanned by
equals the area of the parallelogram spanned by 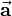 and
and 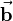 and is calculated as follows:
and is calculated as follows:
In this equation 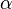 denotes the angle between the two vectors which ranges from
denotes the angle between the two vectors which ranges from 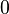 to
to 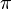 (see figure above). Furthermore it should be noted that the cross product is exclusively defined for the three-dimensional euclidian vector space. Therefore the following computational relationship holds:
(see figure above). Furthermore it should be noted that the cross product is exclusively defined for the three-dimensional euclidian vector space. Therefore the following computational relationship holds:
Based on the described relationships it can be seen, that the commutative law does not hold for the cross product. Instead, the following holds:
Furthermore there are some special cases that lead to simplifications in technical context:
Multimedial educational material
|
http://demonstrations.wolfram.com/CrossProductOfVectorsInTheYZPlane/ Applet: Cross product of two vectors in the yz-plane |
Literature
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Edition (Pearson Studium, 2011)
- Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Edition (Springer Berlin Heidelberg, 2001)
- Wolfgang Pavel und Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Edition (Pearson Studium, 2007)