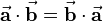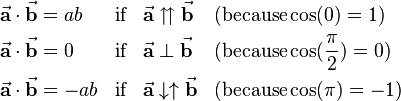Dot product
| ← Back: Simple arithmetic operations | Overview: Vector algebra | Next: Cross product → |
|
|
The dot product of two vectors results in a scalar value and is defined as
where 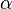 describes the angle between the two vectors which ranges from
describes the angle between the two vectors which ranges from 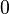 to
to 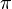 (see figure). The dot product is denoted with a simple point between the vectors or without any sign.
(see figure). The dot product is denoted with a simple point between the vectors or without any sign.
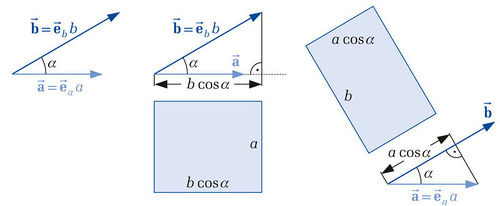
Regarding the right side of the above equation, the following correlation can be noted: If you project the vector 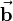 on the vector
on the vector 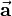 , you get the distance
, you get the distance  . As a consequence the result of the dot product can be seen as the area of a rectangle with the side legths
. As a consequence the result of the dot product can be seen as the area of a rectangle with the side legths 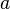 and
and  . The projection can also be done contrariwise (projection of vector
. The projection can also be done contrariwise (projection of vector 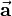 on vector
on vector 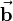 ). So that you get the distance
). So that you get the distance  . The multiplication of this term with
. The multiplication of this term with 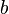 leads to a rectangle with equivalent area but different aspect ratio (see figure).
leads to a rectangle with equivalent area but different aspect ratio (see figure).
Another possibility to compute the dot product is to multiply the corresponding components and sum them up:
In general the dot product of n-dimensional vectors is computed as follows:
which is nothing else than the matrix product of the transpose of the first vector with the second vector denoted in matrix algebra:
On the basis of the described relations it appears, that the commutative law holds:
Furthermore the following special cases can be considered, that often lead to simplifications in technical context:
Multimedial educational material
|
http://demonstrations.wolfram.com/DotProduct/ Applet: Dot product of two vectors (free CDF-Player required) |
Literature
- Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Edition (Springer Berlin Heidelberg, 2001)
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Edition (Pearson Studium, 2011)
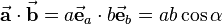
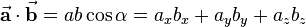
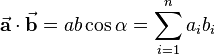
![\vec{\mathbf{a}} \cdot \vec{\mathbf{b}} = \vec{\mathbf{a}}^T \vec{\mathbf{b}} =
\left[\begin{array}{ccc}
a_1 & \dots & a_n
\end{array}\right]
\left[\begin{array}{c}
b_1 \\
\vdots \\
b_n
\end{array}\right] =
\sum_{i=1}^{n} a_i b_i](/wiki/robotics/images/math/3/0/e/30ea414cbbfc92e6f6f8ce984fa32835.png)