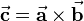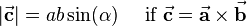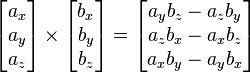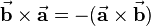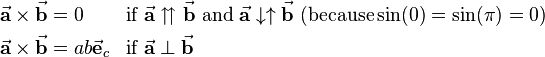Cross product

← Back: Dot product

Overview: Vector algebra

Next: Matrices →

There are exercises as selftest for this article.

You can use MATLAB for the content of this article.

The cross product of two vectors is denoted with an $\times$. The cross product of vector $\vec{\mathbf{a}}$ and vector $\vec{\mathbf{b}}$ results in a new vector

$\vec{\mathbf{c}} = \vec{\mathbf{a}} \times \vec{\mathbf{b}}$

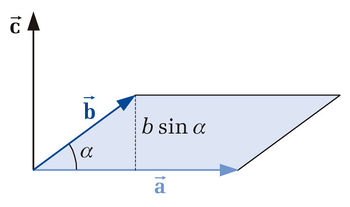
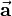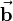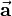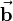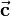that is perpendicular to the surface spanned by vectors $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ (see figure). Furthermore the three vectors $\vec{\mathbf{a}}$, $\vec{\mathbf{b}}$ and $\vec{\mathbf{c}}$ build a rectangular coordinate system based on the right-hand rule. 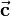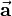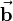The magnitude of vector $\vec{\mathbf{c}}$ equals the area of the parallelogram spanned by $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ and is calculated as follows:

$|\vec{\mathbf{c}}| = a b \sin(\alpha)\ \quad\text{if}\ \vec{\mathbf{c}} = \vec{\mathbf{a}} \times \vec{\mathbf{b}}$

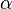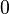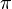In this equation $\alpha$ denotes the angle between the two vectors which ranges from $0$ to $\pi$ (see figure above). Furthermore it should be noted that the cross product is exclusively defined for the three-dimensional euclidian vector space. Therefore the following computational relationship holds:

$\begin{align} \begin{bmatrix} a_x\\ a_y\\ a_z\end{bmatrix} \times \begin{bmatrix} b_x\\ b_y\\ b_z\end{bmatrix} = \begin{bmatrix} a_y b_z - a_z b_y\\ a_z b_x - a_x b_z\\ a_x b_y - a_y b_x\end{bmatrix} \end{align}$

Based on the described relationships it can be seen, that the commutative law does not hold for the cross product. Instead, the following holds:

$\vec{\mathbf{b}} \times \vec{\mathbf{a}} = -(\vec{\mathbf{a}} \times \vec{\mathbf{b}})$

Furthermore there are some special cases that lead to simplifications in technical context:

$\begin{align} \vec{\textbf{a}}\times\vec{\mathbf{b}} &= 0 &\text{if}&\ \vec{\textbf{a}} \upuparrows \vec{\textbf{b}}\ \text{and}\ \vec{\textbf{a}} \downarrow\uparrow \vec{\textbf{b}}\ (\text{because} \sin(0) = \sin(\pi) = 0)\\ \vec{\textbf{a}}\times\vec{\mathbf{b}} &= a b \vec{\textbf{e}}_c &\text{if}&\ \vec{\textbf{a}} \perp \vec{\textbf{b}} \end{align}$

Multimedial educational material

http://demonstrations.wolfram.com/CrossProductOfVectorsInTheYZPlane/ Applet: Cross product of two vectors in the yz-plane

Literature

• Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Edition (Pearson Studium, 2011)
• Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Edition (Springer Berlin Heidelberg, 2001)
• Wolfgang Pavel und Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Edition (Pearson Studium, 2007)