Scaling
From Robotics
| ← Back: Translation | Overview: Transformations | Next: Rotation → |
Scaling shifts coordinates similar to translation. The difference is, that translation is independent of the current coordinates. Scaling however shifts the coordinates depending on the current values. So the same trnasformation matrix has various effects on different vectors.
For the sake of simplicity scaling is explained for two-dimensional space. But the behavior of the parameters is the same for an additional third dimension. Scaling is achieved by modifying the components 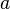 and
and 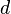 on the first diagonal of the transformation matrix
on the first diagonal of the transformation matrix  , while the other components are zero:
, while the other components are zero:
Several different cases can be considered:
▪ ![\mathbf{T}_0=
\left[\begin{array}{cc}
a=1 & 0\\
0 & d=1
\end{array}\right]](/wiki/robotics/images/math/8/4/7/847276cf390a18f00c26b04325566014.png)
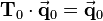
 is the identity matrix → no effect
is the identity matrix → no effect
▪ ![\mathbf{T}_1=
\left[\begin{array}{cc}
a>1 & 0\\
0 & d=1
\end{array}\right]](/wiki/robotics/images/math/5/5/3/5536aa5654711046d3d31d8eba7a6f60.png)
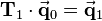
x-component is scaled up → vector shifted to positive x-direction
![\mathbf{T}=
\left[\begin{array}{cc}
a & 0\\
0 & d
\end{array}\right]](/wiki/robotics/images/math/e/4/8/e48fa13a934da9e087066c4d33c43310.png)