Difference between revisions of "Scaling"
From Robotics
| Line 13: | Line 13: | ||
Several different cases can be considered:<br/> | Several different cases can be considered:<br/> | ||
| − | :<table border- | + | :<table style="border-bottom: solid 1px #999999"> |
<tr border: none;> | <tr border: none;> | ||
<td valign="center">▪ </td> | <td valign="center">▪ </td> | ||
| − | <td width="250px" valign="center" align="center | + | <td width="250px" valign="center" align="center"> |
<math> | <math> | ||
| − | \mathbf{T} | + | \mathbf{T}_0= |
\left[\begin{array}{cc} | \left[\begin{array}{cc} | ||
a=1 & 0\\ | a=1 & 0\\ | ||
| Line 25: | Line 25: | ||
</math> | </math> | ||
</td> | </td> | ||
| − | <td valign="center" width="150px" align="center | + | <td valign="center" width="150px" align="center"> |
<math> | <math> | ||
| − | \mathbf{T} | + | \mathbf{T}_0\cdot \vec{\mathbf{q}}_0 = \vec{\mathbf{q}}_0 |
</math> | </math> | ||
</td> | </td> | ||
| Line 33: | Line 33: | ||
<td valign="center"> | <td valign="center"> | ||
<math>\mathbf{T}</math> is the identity matrix → no effect | <math>\mathbf{T}</math> is the identity matrix → no effect | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | <table style="border-bottom: solid 1px #999999"> | ||
| + | <tr border: none;> | ||
| + | <td valign="center">▪ </td> | ||
| + | <td width="250px" valign="center" align="center"> | ||
| + | <math> | ||
| + | \mathbf{T}_1= | ||
| + | \left[\begin{array}{cc} | ||
| + | a>1 & 0\\ | ||
| + | 0 & d=1 | ||
| + | \end{array}\right] | ||
| + | </math> | ||
| + | </td> | ||
| + | <td valign="center" width="150px" align="center"> | ||
| + | <math> | ||
| + | \mathbf{T}_1\cdot \vec{\mathbf{q}}_0 = \vec{\mathbf{q}}_1 | ||
| + | </math> | ||
| + | </td> | ||
| + | <td width="25px"/> | ||
| + | <td valign="center"> | ||
| + | x-component is scaled up → vector shifted to positive x-direction | ||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 16:06, 27 May 2014
| ← Back: Translation | Overview: Transformations | Next: Rotation → |
Scaling shifts coordinates similar to translation. The difference is, that translation is independent of the current coordinates. Scaling however shifts the coordinates depending on the current values. So the same trnasformation matrix has various effects on different vectors.
For the sake of simplicity scaling is explained for two-dimensional space. But the behavior of the parameters is the same for an additional third dimension. Scaling is achieved by modifying the components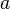 
and 
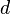on the first diagonal of the transformation matrix 
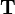, while the other components are zero:
![\mathbf{T}=
\left[\begin{array}{cc}
a & 0\\
0 & d
\end{array}\right]](/wiki/robotics/images/math/e/4/8/e48fa13a934da9e087066c4d33c43310.png)
Several different cases can be considered:
▪ ![\mathbf{T}_0=
\left[\begin{array}{cc}
a=1 & 0\\
0 & d=1
\end{array}\right]](/wiki/robotics/images/math/8/4/7/847276cf390a18f00c26b04325566014.png)
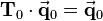
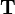is the identity matrix → no effect
▪ ![\mathbf{T}_1=
\left[\begin{array}{cc}
a>1 & 0\\
0 & d=1
\end{array}\right]](/wiki/robotics/images/math/5/5/3/5536aa5654711046d3d31d8eba7a6f60.png)
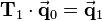
x-component is scaled up → vector shifted to positive x-direction
