Zylinderkoordinaten: Unterschied zwischen den Versionen
| Zeile 50: | Zeile 50: | ||
</math> | </math> | ||
|} | |} | ||
| + | |||
Umgekehrt lassen sich auch Zylinderkoordinaten aus gegebenen kartesischen Koordinaten berechnen: | Umgekehrt lassen sich auch Zylinderkoordinaten aus gegebenen kartesischen Koordinaten berechnen: | ||
Version vom 29. August 2012, 13:28 Uhr
To-do:
- Formulierungen überarbeiten
- Verallgemeinerung zu krOrthKoor ggf. entfernen
Neu
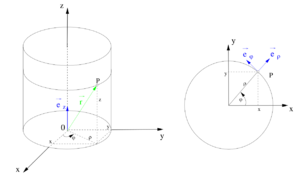
Das Zylinderkoordinatensystem ermöglicht insbesondere dann eine kompakte Beschreibung von Positionen und gerichteten Größen im Raum, wenn man es mit zylinderförmigen Anordnungen zu tun hat. Das elektrische Feld einer Linienladung, die näherungsweise als zylinderförmig angenommen werden kann, lässt sich zum Beispiel wesentlich einfacher in Zylinder- als in kartesischen Koordinaten beschreiben (vgl. Beispiel unten). Es gibt zahlreiche weitere Beispiele wie die Beschreibung des elektrischen Feldes einer zylinderförmigen Raumladung oder die Beschreibung des magnetischen Feldes eines stromdurchflossenen Leiters.
Bei den Zylinderkoordinaten wird ein Punkt 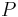 im Raum durch die drei Koordinaten
im Raum durch die drei Koordinaten 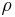 ,
,  und
und 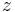 beschrieben. Dabei bleibt die
beschrieben. Dabei bleibt die 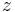 -Achse des kartesischen Koordinatensystems unverändert erhalten.
-Achse des kartesischen Koordinatensystems unverändert erhalten. 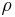 (je nach Quelle auch als
(je nach Quelle auch als  bezeichnet) gibt den Abstand zur
bezeichnet) gibt den Abstand zur 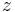 -Achse an und
-Achse an und  bezeichnet den Winkel zum betrachteten Punkt. Dabei wird
bezeichnet den Winkel zum betrachteten Punkt. Dabei wird  ausgehend von der positiven
ausgehend von der positiven 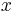 -Achse in Richtung der positiven
-Achse in Richtung der positiven 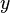 -Achse gezählt. Somit ist der positiven
-Achse gezählt. Somit ist der positiven 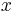 -Achse der Winkel
-Achse der Winkel 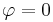 und der negativen
und der negativen 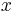 -Achse der Winkel
-Achse der Winkel  zugeordnet.
zugeordnet.
Die Richtung der Einheitsvektoren 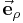 und
und 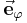 hängt von der Position des betrachteten Punktes ab. Die nebenstehende Abbildung verdeutlicht, dass
hängt von der Position des betrachteten Punktes ab. Die nebenstehende Abbildung verdeutlicht, dass 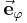 immer tangential zu dem Kreisbogen (
immer tangential zu dem Kreisbogen ( -Koordinatenlinie) im Punkt
-Koordinatenlinie) im Punkt 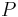 verläuft und
verläuft und  immer orthogonal auf diesem Kreisbogen steht. Der Einheitsvektor
immer orthogonal auf diesem Kreisbogen steht. Der Einheitsvektor 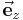 (vgl. kartesische Koordinaten) zeigt unabhängig vom betrachteten Punkt im Raum immer in dieselbe Richtung.
(vgl. kartesische Koordinaten) zeigt unabhängig vom betrachteten Punkt im Raum immer in dieselbe Richtung.
Betrachtet man ausschließlich die 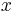 -
-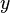 -Ebene ohne die
-Ebene ohne die 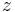 -Achse, so handelt es sich um Polarkoordinaten.
-Achse, so handelt es sich um Polarkoordinaten.
Die Koordinaten und Einheitsvektoren der verschiedenen Koordinatensysteme können mit Hilfe von Transformationsgleichungen ineinander umgerechnet werden (siehe hierzu Formelsammlung Koordinatensysteme). Möchte man beispielsweise den Wert 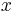 in kartesischen Koordinaten eines in Zylinderkoordinaten gegebenen Punktes
in kartesischen Koordinaten eines in Zylinderkoordinaten gegebenen Punktes 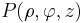 ermitteln, so bietet sich die Verwendung trigonometrischer Funktionen an. Aus der Abbildung wird ersichtlich, dass
ermitteln, so bietet sich die Verwendung trigonometrischer Funktionen an. Aus der Abbildung wird ersichtlich, dass 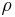 der Hypotenuse und
der Hypotenuse und 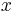 der Ankathete in Bezug auf das durch
der Ankathete in Bezug auf das durch  gegebene rechtwinklige Dreieck entspricht. Damit gilt:
gegebene rechtwinklige Dreieck entspricht. Damit gilt:
Für die 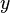 -Koordinate kann analog verfahren werden und die
-Koordinate kann analog verfahren werden und die 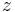 -Koordinate bleibt erhalten, so dass sich folgende Transformationsgleichungen ergeben:
-Koordinate bleibt erhalten, so dass sich folgende Transformationsgleichungen ergeben:
| Umrechnung von Zylinder- in kartesische Koordinaten |
|
|
| |
|
|
Umgekehrt lassen sich auch Zylinderkoordinaten aus gegebenen kartesischen Koordinaten berechnen:
| Umrechnung von kartesischen- in Zylinderkoordinaten |
|
|
| |
|
|
Alt
Betrachtet man das Modell eines Kabels, ist es häufig problematisch, Effekte mathematisch im gewohnten kartesischen Koordinatensystem zu beschreiben. Durch die Wölbung der Oberfläche muss im kartesischen System immer ein sich verändernder Winkel mitbetrachtet werden, selbst wenn die Effekte, die man beschreiben will, senkrecht oder parallel zu dem Kabel verlaufen. Um sich die Rechnung zu vereinfachen, wählt man insbesondere für Probleme mit konzentrischen oder radialen Anordnungen einen Sonderfall der krummlinigen orthogonalen Koordinatensysteme, die Zylinderkoordinaten:
Um die Zylinderkoordinaten zu verstehen, hilft es, sich einen Zylinder vorzustellen und ihn in seine Bestandteile, also Deckel und Mantelflächen zu unterteilen. Die Deckelfläche lässt sich dabei am einfachsten mit ihrem Radius 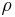 und dem Winkel
und dem Winkel  beschreiben (siehe Abbildung). Eben diese Koordinaten werden bei den ebenen Zylinderkoordinaten (auch: Polarkoordinaten) verwendet. Dabei wird der Winkel
beschreiben (siehe Abbildung). Eben diese Koordinaten werden bei den ebenen Zylinderkoordinaten (auch: Polarkoordinaten) verwendet. Dabei wird der Winkel  definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt.
Um die Höhe berücksichtigen zu können, wählt man die z-Koordinate, die schon aus den kartesischen Koordinaten bekannt ist. Diese entspricht der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen.
definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt.
Um die Höhe berücksichtigen zu können, wählt man die z-Koordinate, die schon aus den kartesischen Koordinaten bekannt ist. Diese entspricht der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen.
Aufgepasst:Im Gegensatz zu den Einheitsvektoren der kartesischen Koordinaten verändern die Einheitsvektoren der Zylinderkoordinaten ( und
und 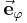 ) ihre Richtung mit wachsenden Koordinatenwerten. Aus der Abbildung wird klar, dass
) ihre Richtung mit wachsenden Koordinatenwerten. Aus der Abbildung wird klar, dass 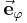 immer tangential zu dem Kreisbogen im Punkt P verläuft und
immer tangential zu dem Kreisbogen im Punkt P verläuft und  immer orthogonal auf dem Kreisbogen steht.
immer orthogonal auf dem Kreisbogen steht.
Um zwischen Koordinatensystemen wechseln zu können, braucht man die Transformationsgleichungen. Zur Berechnung verwendet man die Trigonometrischen Funktionen. Als Beispiel soll die Koordinate x durch die Zylinderkoordinaten dargestellt werden. Dazu benötigt man die Parameter 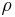 und
und  , da die z-Koordinate in beiden Systemen äquivalent ist. Betrachtet man nun die Abbildung, erkennt man, dass
, da die z-Koordinate in beiden Systemen äquivalent ist. Betrachtet man nun die Abbildung, erkennt man, dass 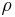 der Hypotenuse und x der Ankathete entspricht:
der Hypotenuse und x der Ankathete entspricht:
Stellt man diese Gleichung nach x um, erhält man die erste Transformationsgleichung. Die zweite Transformationsgleichung ergibt sich aus der selben Überlegung, nur entspricht die y-Achse der Gegenkathete, daher erhält man den Sinus in der zweiten Gleichung:
| Transformationsgleichung |
|
|
| |
|
|
Möchte man aus dem Zylinderkoordinatensystem wieder in das kartesische Koordinatensystem zurücktransformieren, muss man die oberen Tranformationsgleichungen umstellen und man erhält entsprechend:
| Transformationsgleichung |
|
|
| |
|
|
Nur die Transformationsgleichungen reichen nicht, um die kartesischen Koordinaten durch Zylinderkoordinaten auszudrücken, da die Einheitsvektoren nach wie vor kartesisch dargestellt werden. Um auch sie umzuwandeln, kann man folgende Form verwenden:
Hier wird also der Ortsvektor (Ein Vektor, der vom Ursprung bis zu den Punkten im Raum verläuft. Die Berechnung des Ortsvektors wird im unteren Beispiel veranschaulicht. Hier genügt es zu wissen, dass der Ortsvektor in kartesischen Koordinaten folgende Funktion besitzt: 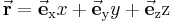 ) nach der jeweiligen Koordinate abgeleitet und durch den Metrikkoeffizienten
) nach der jeweiligen Koordinate abgeleitet und durch den Metrikkoeffizienten 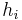 geteilt.
geteilt.
Anschaulich bedeutet das, dass die partielle Ableitung des Ortsvektors nach der jeweiligen Koordinate gesucht ist. Diese ist nichts weiter als die Änderungsgeschwindigkeit des Ortsvektors, also wie schnell sich dieser bei dem Verändern der Koordinate "bewegt" oder wie stark die Änderung des Einheitsvektors von Punkt zu Punkt ist.
Da Einheitsvektoren so definiert sind, dass sie immer die Länge 1 haben müssen, wird der Einheitsvektor noch normiert. Dazu verwendet man den Metrikkoeffizienten, da dieser den Betrag der Änderung des Ortsvektors bestimmt. Übrig bleibt ein Vektor in Richtung der Änderung mit dem Betrag eins.
Zur Veranschalichung der Rechnung wird sie hier anhand eines Beispiels der Koordinate  aufgeschlüsselt.
aufgeschlüsselt.
Zunächst wird der Metrikkoeffizient berechnet, dazu müssen für die Variablen x,y,z die Transformationsgleichungen eingesetzt und nach der Koordinate  differenziert werden. Anschließend wird der Betrag gebildet:
differenziert werden. Anschließend wird der Betrag gebildet:
Die beiden anderen metrischen Koeffizienten ergeben sich zu:
Hat man nun die Metrikkoeffizienten oder metrischen Faktoren, kann man die Einheitsvektoren des Zylinderkoordinatensystems bestimmen. Dazu leitet man wie schon bei dem Metrikkoeffizienten den Ortsvektor nach der gesuchten Koordinate ab und man erhält:
| Einheitsvektoren |
|
|
| |
|
|
Zwei weitere wichtige Parameter im Zylinderkoordinatensystem sind das vektorielle Wegelement:
und das Volumenelement:
Warum es sich lohnt eine Koordinatentransformation durchzuführen, soll anhand dieses Beispiels verdeutlicht werden. Hier soll der Ortsvektor, eine Funktion, bei der der Vektor vom Koordinatenursprung auf einen Punkt abgebildet wird, in zylindrischen Koordinaten ausgedrückt werden, da diese Darstellung in Zylinderkoordinaten viel übersichtlicher ist, als die Darstellung in den kartesischen Koordinaten. Dafür sei der Ortsvektor Als erstes drückt man diesen Vektor in zylindrischen Koordinaten mithilfe der Transformationsgleichungen aus und fasst die ersten beiden Terme zusammen: Vergleicht man die Beziehungen mit den Einheitsvektoren des Zylinderkoordinatensystems, sieht man sofort, dass die kartesischen Einheitsvektoren Durch einsetzen des Einheitsvektors |
Multimediale Lehrmaterialien
|
http://www.pha.jhu.edu/~javalab/cylindrical/cylindrical.html Applet: Punkt in Zylinderkoordinaten (engl.) http://demonstrations.wolfram.com/ExploringCylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://demonstrations.wolfram.com/CylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) |
Hilfreiche Links
|
http://www.math.wpi.edu/Course_Materials/MA2251C99/images/cylndrcl.gif Bild zu infinitesimalen Volumenelement in Zylinderkoordinatensystem http://lh5.ggpht.com/_XvrTyMj5b-k/SaH0PTc-qWI/AAAAAAAAFnM/YYo0W-gT_5I/controlvolumecylindricalcontinuity5.png Bild zu einem infinitesimalen Volumenelement in Zylinderkoordinaten http://scientificsentence.net/Electromagnetics/index.php?key=yes&Integer=Cylindrical Bild und Erläuterung zu den Einheitsvektoren im Zylinderkoordinatensystem (engl.) |
| ← Zurück: Das kartesische Koordinatensystem | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Kugelkoordinaten → |
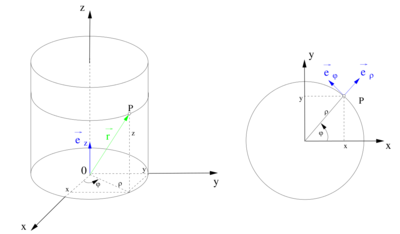
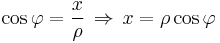
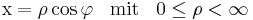
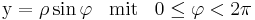
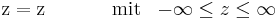
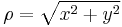
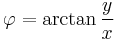

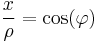
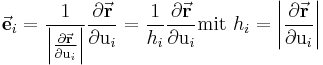
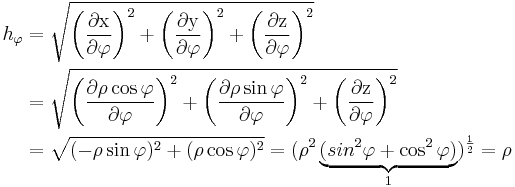
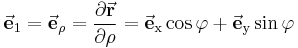
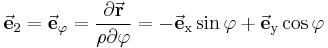

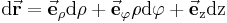
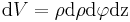
 in kartesischen Koordinaten gegeben:
in kartesischen Koordinaten gegeben:

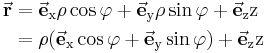
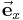 und
und 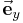 sich im zylindrischen System in dem Einheitsvektor
sich im zylindrischen System in dem Einheitsvektor