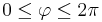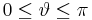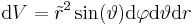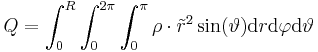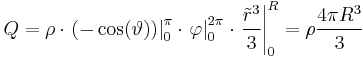Infinitesimale Weg-, Flächen-, und Volumenelemente: Unterschied zwischen den Versionen
(→Flächenelemente) |
(→Flächenelemente) |
||
| Zeile 40: | Zeile 40: | ||
Es muss bei der [[Vektorrechnung:Übersicht| vektoriellen]] Integration auch auf die Orientierung der Fläche geachtet werden. Dazu '''definiert''' man eine Flächennormale ('''man weiß nicht, was das ist'''), die orthogonal auf dem Flächenstück steht. | Es muss bei der [[Vektorrechnung:Übersicht| vektoriellen]] Integration auch auf die Orientierung der Fläche geachtet werden. Dazu '''definiert''' man eine Flächennormale ('''man weiß nicht, was das ist'''), die orthogonal auf dem Flächenstück steht. | ||
| − | Wenn die Flächenelemente gekrümmt sind, dann müssen zur Berechnung der Flächenelemente so genannte ''Korrekturfaktoren'' eingeführt werden. Als Beispiel betrachtet man eine Kreisringfläche in der x-y Ebene. Möchte man dort ein infinitesimales Flächenelement bestimmen, so reicht es nicht aus einfach <math>\mathrm{d}x\mathrm{d}y</math> zu verwenden. Durch die Krümmung der Fläche würde der Fehler sehr groß werden. Es bietet sich eine Koordinatentransformation in [[Zylinderkoordinaten|Polarkoordinaten]] an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden. | + | Wenn die Flächenelemente gekrümmt sind, dann müssen zur Berechnung der Flächenelemente ('''des Flächeninhalts?''') so genannte ''Korrekturfaktoren'' eingeführt werden. Als Beispiel betrachtet man eine Kreisringfläche in der x-y Ebene. Möchte man dort ein infinitesimales Flächenelement bestimmen, so reicht es nicht aus einfach <math>\mathrm{d}x\mathrm{d}y</math> zu verwenden. Durch die Krümmung der Fläche würde der Fehler sehr groß werden. Es bietet sich eine Koordinatentransformation in [[Zylinderkoordinaten|Polarkoordinaten]] an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden. |
'''dA = ??? Der Grafik hinzufügen!''' | '''dA = ??? Der Grafik hinzufügen!''' | ||
Version vom 24. Juli 2012, 16:55 Uhr
To-do:
- Formulierungen überarbeiten (insbes. fett)
- Hinweise zur Integrationsrichtung einfügen
- x-Achse im Bild "Raumladung einer Kugel" verlängern (sieht sonst perspektivisch falsch aus) und Farbton ändern
- Integration über Stromdichte mit zum Durchflutungsgesetz schreiben und darauf eingehen, da dann sowohl ein Kontur und ein Flächenintergral abgedeckt wird.
Viele wichtige Zusammenhänge in der Elektrotechnik sind mit Integralsätzen formuliert, wie zum Beispiel der Satz von Gauß, das Durchflutungsgesetz oder das Induktionsgesetz. Dabei wird immer über eine Kontur oder eine Fläche integriert. Um diese Konturen oder Flächen richtig zu beschreiben benötigt man infinitesimale (Herkunft des Wortes) Elemente.
Betrachtet man das Durchflutungsgesetz, welches das Linienintegral der magnetischen Feldstärke um eine geschlossene Kurve C in Beziehung zum Strom setzt, der durch die von dieser Kurve eingeschlossene Fläche fließt (Satz endet nicht richtig):
An dieser Stelle soll es aber unter anderem um das Wegelement 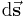 gehen.
Man erkennt in den jeweiligen Integralen, ob man über einen Weg, eine Fläche oder ein Volumen integriert, indem man das Differential am Ende des Integrals betrachtet. Es kann die Fom
gehen.
Man erkennt in den jeweiligen Integralen, ob man über einen Weg, eine Fläche oder ein Volumen integriert, indem man das Differential am Ende des Integrals betrachtet. Es kann die Fom 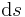 ,
,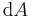 oder
oder 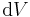 annehmen.
annehmen.
Inhaltsverzeichnis
Wegelemente
Betrachtet man in der Abbildung das Wegelement 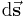 , so fällt auf, dass es in beliebige Richtungen zeigt (hä? woran soll das hier auffallen?), ebenso wie auch die Kontur im Durchflutungssatz eine beliebige (nein, sie muss zumindest geschlossen sein, also isrt sie nicht beliebig) Form annehmen kann. Wichtig ist hierbei, dass das Wegelement
, so fällt auf, dass es in beliebige Richtungen zeigt (hä? woran soll das hier auffallen?), ebenso wie auch die Kontur im Durchflutungssatz eine beliebige (nein, sie muss zumindest geschlossen sein, also isrt sie nicht beliebig) Form annehmen kann. Wichtig ist hierbei, dass das Wegelement 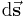 als infinitesimales Wegstück aufgefasst werden soll. Es ist also ein sehr kleines Wegstück, so klein, dass die Krümmung des einzelnen Wegstücks vernachlässigbar wird.
als infinitesimales Wegstück aufgefasst werden soll. Es ist also ein sehr kleines Wegstück, so klein, dass die Krümmung des einzelnen Wegstücks vernachlässigbar wird.
In den nebenstehenden Abbildungen (nebenstehend sind keine Abbildungen) sind zwei beispielhafte Verläufe einer Linienladung dargestellt. Im ersten Fall verläuft die Linienladung nur entlang der x-Achse. Das Wegelement kann hier also mit dem Differential 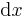 dargestellt (wirklich dargestellt?) werden, da die zu integrierenden Funktion
dargestellt (wirklich dargestellt?) werden, da die zu integrierenden Funktion 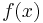 nur von x abhängt.
nur von x abhängt.
Ist jedoch der Kurvenverlauf aus der zweiten Abbildung gegeben, ist die Funktion von x und y abhängig 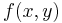 . Nun kann man nicht einfach nach
. Nun kann man nicht einfach nach 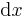 und
und 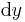 integrieren, weil so eine Fläche aufgespannt wird und man so ein Flächenelement
integrieren, weil so eine Fläche aufgespannt wird und man so ein Flächenelement 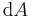 erhält (Argumentation des letzten Satzes unschlüssig). Da hier ein Kreisbogen betrachtet wird, bietet sich die Verwendung von Polarkoordinaten, da so der Kreisbogen nur noch von einner Koordinaten
erhält (Argumentation des letzten Satzes unschlüssig). Da hier ein Kreisbogen betrachtet wird, bietet sich die Verwendung von Polarkoordinaten, da so der Kreisbogen nur noch von einner Koordinaten  abhängt (1. Du sprechen Deutsch? 2. "Der Kreisbogen" ist doch Quatsch. Ist die LÄNGE DES KREISBOGENS gemeint?).
abhängt (1. Du sprechen Deutsch? 2. "Der Kreisbogen" ist doch Quatsch. Ist die LÄNGE DES KREISBOGENS gemeint?).
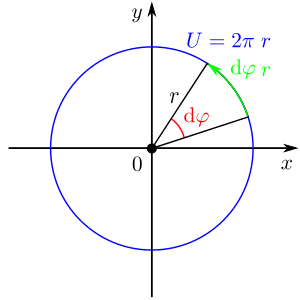
Es muss darauf geachtet werden, dass vor allem bei den gekrümmten orthogonalen Koordinaten oft Korrekturfaktoren (Man weiß doch gar nicht, was Korrekturfaktoren sein sollen!) bei infinitesimalen Elementen zu berücksichtigen sind. Hier ist die Koordinate  auch vom Radius r abhängig. Dies entspricht einer Umfangsberechnung des Kreises. Der Kreis hat einen Gesamtumfang von
auch vom Radius r abhängig. Dies entspricht einer Umfangsberechnung des Kreises. Der Kreis hat einen Gesamtumfang von 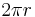 . Betrachtet man ein kleines Teilstück des Kreises folgt:
. Betrachtet man ein kleines Teilstück des Kreises folgt: 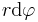 (In Grafik untereinander darstellen).
(In Grafik untereinander darstellen).
In dieser Vorlesung werden nur einfache Verläufe entlang der Koordinatenachsen uns bekannter Koordinatensysteme verwendet (stimmt nicht!!!). Für kompliziertere Verläufe gibt es (besser: existieren) mathematische Hilfsmittel, auf die hier aber nicht näher eingegangen werden soll (wird!). Es werden hauptsächlich für Wegelemente in den kartesischen Koordinaten 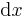 ,
,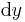 oder
oder 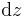 , in den Zylinderkoordinaten
, in den Zylinderkoordinaten 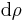 oder
oder 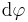 und in den Kugelkoordinaten
und in den Kugelkoordinaten 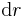 verwendet (Du sprechen Deutsch?).
verwendet (Du sprechen Deutsch?).
Flächenelemente
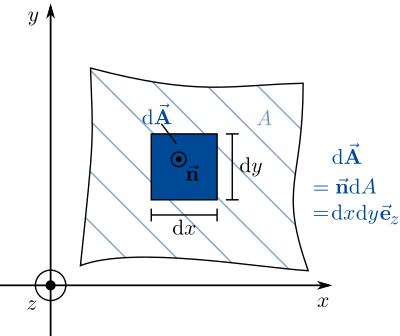
Im einfachsten Fall sind die zu bestimmenden Flächenelemente in kartesischen Koordinaten gegeben (wenn sie gegeben sind, müssen sie wohl nicht mehr bestimmt werden). Zunächst ist hier eine Integrationsfläche (was soll denn eine Integrationsfläche sein?) zu sehen, die sich in x-und y-Richtung ausbreitet. Ein infinitesimales Teilstück dieser Fläche muss dem zufolge auch in beide Richtungen ausgedehnt sein, um die gesamte Fläche beschreiben zu können (Argumentation unschlüssig). Eine Integration über 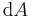 , kann dann auch als Integration über beide Wegelemente
, kann dann auch als Integration über beide Wegelemente 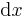 und
und 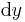 beschrieben werden, wie auch bei nicht infinitesimal kleinen Objekten sich die Fläche aus dem Produkt der Seiten x und y bestimmt.
beschrieben werden, wie auch bei nicht infinitesimal kleinen Objekten sich die Fläche aus dem Produkt der Seiten x und y bestimmt.
Es muss bei der vektoriellen Integration auch auf die Orientierung der Fläche geachtet werden. Dazu definiert man eine Flächennormale (man weiß nicht, was das ist), die orthogonal auf dem Flächenstück steht.
Wenn die Flächenelemente gekrümmt sind, dann müssen zur Berechnung der Flächenelemente (des Flächeninhalts?) so genannte Korrekturfaktoren eingeführt werden. Als Beispiel betrachtet man eine Kreisringfläche in der x-y Ebene. Möchte man dort ein infinitesimales Flächenelement bestimmen, so reicht es nicht aus einfach 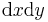 zu verwenden. Durch die Krümmung der Fläche würde der Fehler sehr groß werden. Es bietet sich eine Koordinatentransformation in Polarkoordinaten an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden.
dA = ??? Der Grafik hinzufügen!
zu verwenden. Durch die Krümmung der Fläche würde der Fehler sehr groß werden. Es bietet sich eine Koordinatentransformation in Polarkoordinaten an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden.
dA = ??? Der Grafik hinzufügen!
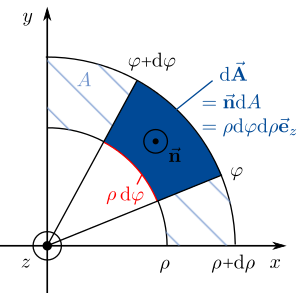
Zur Bestimmung des Korrekturfaktors oder auch Metrikkoeffizienten betrachtet man nun ein Flächenelement des Kurvenstücks (vgl. Abbildung). Die Seitenlänge des Flächenelements entlang der r-Koordinate ist nicht gekrümmt und kann daher als 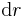 angenommen werden. Die
angenommen werden. Die  -Koordinate hängt auch von dem Radius r ab. Deshalb ist das infinitesimale Flächenelement einer Kreisfläche
-Koordinate hängt auch von dem Radius r ab. Deshalb ist das infinitesimale Flächenelement einer Kreisfläche 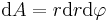 .
.
Volumenelemente
Betrachtet man das Volumenelement in kartesischen Koordinaten ändert sich nicht viel im vergleich zu dem Flächenelement in kartesischen Koordinaten (GEHT GAR NICHT!!!). Es muss nur auch noch die Ausdehnung in z-Richtung berücksichtigt werden. Also ergibt sich ein infitesimales Volumenelement in kartesischen Koordinaten zu:
Aus ähnlichen Betrachtungen ergeben sich die Volumenelemente, die in den Abbildungen zu sehen sind:
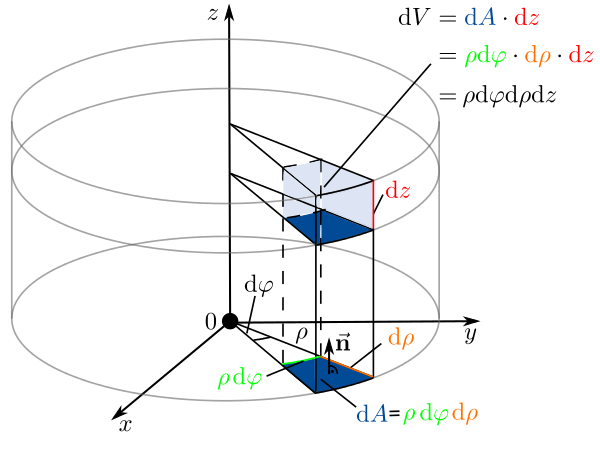
Das Flächenelement einer Kreisfläche wurde schon besprochen. Bei dem Volumenelement in Zylinderkoordinaten wird zu diesem Flächenelement, wie in der Abbildung zu sehen, noch eine Höhenkomponente in z-Richtung multipliziert. Daher lautet das Volumenelement:
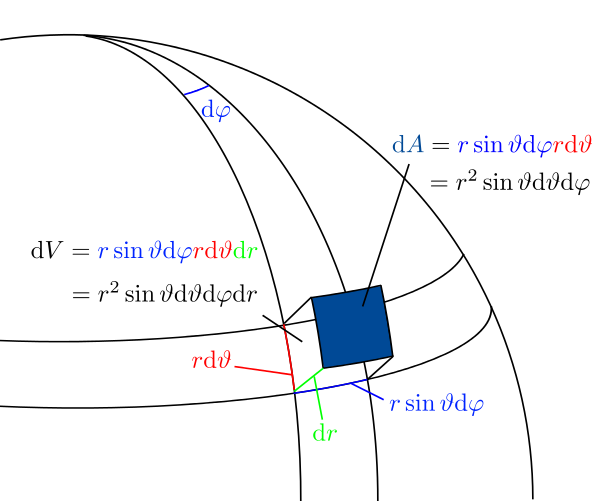
Das Volumenelement der Kugelkoordinaten ergibt sich aus der Symmetrie einer Kugel. Wie in der Abbildung zu sehen kann man die verschiedenen Kanten des Volumenelementes mit den Koordinatenabhängigkeiten beschreiben. So ergibt beisielsweise die Höhen Seite 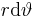 aus den Zusammenhängen, die schon bei den kreisförmigen Wegelementen beschreiben wurden. Multipliziert man alle Abhängigkeiten auf ergibt sich das Volumenelement zu:
aus den Zusammenhängen, die schon bei den kreisförmigen Wegelementen beschreiben wurden. Multipliziert man alle Abhängigkeiten auf ergibt sich das Volumenelement zu:
In diesem Beispiel ist eine homogene Raumladungsdichte Das Volumenelement der kartesischen Koordinaten lautet: Es kann direkt in die Gleichung eingesetzt und das Integral gelöst werden. Da die Raumladungsdichte |
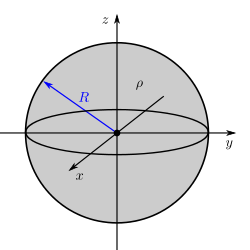
Im zweiten Beispiel wird eine eine kugelförmige, konstante Raumladungsdichte Um über die gesamte Kugel zu integrieren, muss man die Integrationsgrenzen korrekt wählen. Da die gesamte Kugel betrachtet wird, muss die maximalen Ausdehnungen der Kugelkoordinaten für die Winkel Außerdem muss das Volumenelement in Kugelkoordinaten verwendet werden. Dies ergibt sich aus der Symmetrie, zu:
Da Dies enspricht abgesehen von der Konstante |
Multimediale Lehrmaterialien
|
http://highered.mcgraw-hill.com/sites/0073451342/student_view0/chapter13/section6/cylindrical_coordinates__app_.html Darstellung von infinitesimalen Volumenelementen in Zylinderkoordinaten (engl.) |
Hilfreiche Links
|
http://web.mit.edu/8.02t/www/materials/modules/ReviewB.pdf Bebilderte Erklärung zu Kartesischen-, Kugel-, und Zylinderkoordinatensystemen und deren infinitesimalen Elementen (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Klaus Jänich Mathematik 1 Geschrieben für Physiker,2. Auflage (Springer Berlin Heidelberg, 2005)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Hempel, "Mathematische Grundlagen", Linienintegral, Universität Magdeburg
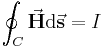

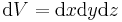
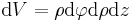
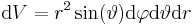
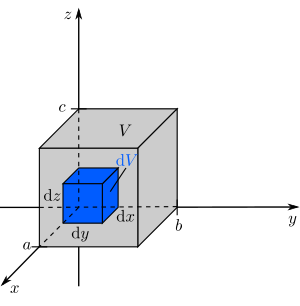
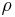 in einem Quader mit den Kantenlängen a, b und c gegeben. Die Raumladungsdichte ist bestimmt als Ladung pro Volumen, daher muss, um die Gesamtladung zu bestimmen, über das Volumen des Quaders integriert werden:
in einem Quader mit den Kantenlängen a, b und c gegeben. Die Raumladungsdichte ist bestimmt als Ladung pro Volumen, daher muss, um die Gesamtladung zu bestimmen, über das Volumen des Quaders integriert werden:
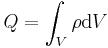
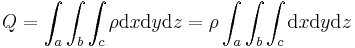
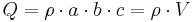
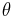 und
und 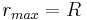 :
: