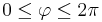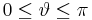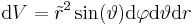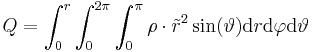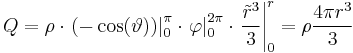Infinitesimale Weg-, Flächen-, und Volumenelemente: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
Ebenso muss der Weg richtig ausgedrückt werden. In den nebenstehenden Abbildungen sind zwei beispielhafte Verläufe einer Linienladung dargestellt. Im ersten Fall verläuft die Linienladung nur entlang der x-Achse. Das Wegelement kann hier also sehr simpel mit dem Differential <math>\mathrm{d}x</math> dargestellt werden, da die zu integrierenden Funktion <math>f(x)</math> nur von ''x'' abhängt. Ist jedoch der Kurvenverlauf aus der zweiten Abbildung gegeben, ist die Funktion von x und y abhängig <math>f(x,y)</math>. Nun kann man aber nicht einfach nach <math>\mathrm{d}x</math> und <math>\mathrm{d}y</math> integrieren, weil man so eine Fläche aufspannen würde und so ein Flächenelement <math>\mathrm{d}A</math> erhält. Deshalb wird in solchen Fällen das Wegelement <math>\mathrm{d}s</math> verwendet, weil es unabhängig von den jeweiligen Koordinaten ist. Das Wegelement <math>\mathrm{d}s</math> kann man sich als kleines Stück genau entlang des Weges vorstellen losgelöst von den jeweiligen Koordinatensystemen. Um solch einen komplizerten Weg konkret auszudrücken, gibt es mehrer Möglichkeiten. In dieser Vorlesung werden aber nur einfache Verläufe entlang der Koordinatenachsen uns bekannter [[Orthogonale Koordinatensysteme:Übersicht|Koordinatensysteme]] verwendet. Für kompliziertere Verläufe gibt es mathematische Hilfsmittel auf die hier aber nicht näher eingegangen werden soll. Es werden hauptsächlich für Wegelemente in den kartesischen Koordinaten <math>\mathrm{d}x</math>,<math>\mathrm{d}y</math> oder <math>\mathrm{d}z</math>, in den Zylinderkoordinaten <math>\mathrm{d}\rho</math> oder <math>\mathrm{d}\varphi</math> und in den Kugelkoordinaten <math>\mathrm{d}r</math> verwendet. | Ebenso muss der Weg richtig ausgedrückt werden. In den nebenstehenden Abbildungen sind zwei beispielhafte Verläufe einer Linienladung dargestellt. Im ersten Fall verläuft die Linienladung nur entlang der x-Achse. Das Wegelement kann hier also sehr simpel mit dem Differential <math>\mathrm{d}x</math> dargestellt werden, da die zu integrierenden Funktion <math>f(x)</math> nur von ''x'' abhängt. Ist jedoch der Kurvenverlauf aus der zweiten Abbildung gegeben, ist die Funktion von x und y abhängig <math>f(x,y)</math>. Nun kann man aber nicht einfach nach <math>\mathrm{d}x</math> und <math>\mathrm{d}y</math> integrieren, weil man so eine Fläche aufspannen würde und so ein Flächenelement <math>\mathrm{d}A</math> erhält. Deshalb wird in solchen Fällen das Wegelement <math>\mathrm{d}s</math> verwendet, weil es unabhängig von den jeweiligen Koordinaten ist. Das Wegelement <math>\mathrm{d}s</math> kann man sich als kleines Stück genau entlang des Weges vorstellen losgelöst von den jeweiligen Koordinatensystemen. Um solch einen komplizerten Weg konkret auszudrücken, gibt es mehrer Möglichkeiten. In dieser Vorlesung werden aber nur einfache Verläufe entlang der Koordinatenachsen uns bekannter [[Orthogonale Koordinatensysteme:Übersicht|Koordinatensysteme]] verwendet. Für kompliziertere Verläufe gibt es mathematische Hilfsmittel auf die hier aber nicht näher eingegangen werden soll. Es werden hauptsächlich für Wegelemente in den kartesischen Koordinaten <math>\mathrm{d}x</math>,<math>\mathrm{d}y</math> oder <math>\mathrm{d}z</math>, in den Zylinderkoordinaten <math>\mathrm{d}\rho</math> oder <math>\mathrm{d}\varphi</math> und in den Kugelkoordinaten <math>\mathrm{d}r</math> verwendet. | ||
| − | [[Datei:Flaechenelement.svg|thumb|right|Flächenelement in kartesischen Koordinaten]] | + | [[Datei:Flaechenelement.svg|350px|thumb|right|Flächenelement in kartesischen Koordinaten]] |
Um in den jeweiligen Integralen deutlich zu machen, dass man über einen Weg, eine Fläche oder ein Volumen integriert, wird an das Integral ein '''Differential''' <math>\mathrm{d}s</math>,<math>\mathrm{d}A</math> oder <math>\mathrm{d}V</math> angehängt. | Um in den jeweiligen Integralen deutlich zu machen, dass man über einen Weg, eine Fläche oder ein Volumen integriert, wird an das Integral ein '''Differential''' <math>\mathrm{d}s</math>,<math>\mathrm{d}A</math> oder <math>\mathrm{d}V</math> angehängt. | ||
Version vom 3. Juni 2012, 13:17 Uhr
Das Durchflutungsgesetz in der Elektrotechnik lautet:
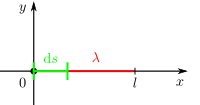
Das Gesetz setzt das Linienintegral des magnetischen Feldes um eine geschlossene Kurve C in Beziehung zum Strom, der durch die von dieser Kurve eingeschlossene Fläche fließt.
Weitere Informationen zur Integration ist bei dem Artikel Erweiterung der Integralrechnung zu finden. An dieser Stelle soll es aber unter anderem um das Wegelement 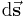 gehen.
Betrachtet man in der Abbildung das Wegelement
gehen.
Betrachtet man in der Abbildung das Wegelement 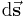 , so fällt auf, dass es in beliebige Richtungen zeigt, ebenso wie auch die Kontur im Durchflutungssatz eine beliebige Form annehmen kann. Wichtig ist hierbei, dass das Wegelement
, so fällt auf, dass es in beliebige Richtungen zeigt, ebenso wie auch die Kontur im Durchflutungssatz eine beliebige Form annehmen kann. Wichtig ist hierbei, dass das Wegelement 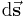 als infinitesimales Wegstück aufgefasst werden soll. Es ist also ein sehr kleines Wegstück, so klein, dass die Krümmung des einzelnen Wegstücks vernachlässigbar wird. So können alle Wegstücke aufsummiert werden und man erhält, wie bei der Herleitung des Integrals die gesamte Kontur
als infinitesimales Wegstück aufgefasst werden soll. Es ist also ein sehr kleines Wegstück, so klein, dass die Krümmung des einzelnen Wegstücks vernachlässigbar wird. So können alle Wegstücke aufsummiert werden und man erhält, wie bei der Herleitung des Integrals die gesamte Kontur
Ebenso muss der Weg richtig ausgedrückt werden. In den nebenstehenden Abbildungen sind zwei beispielhafte Verläufe einer Linienladung dargestellt. Im ersten Fall verläuft die Linienladung nur entlang der x-Achse. Das Wegelement kann hier also sehr simpel mit dem Differential 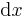 dargestellt werden, da die zu integrierenden Funktion
dargestellt werden, da die zu integrierenden Funktion 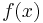 nur von x abhängt. Ist jedoch der Kurvenverlauf aus der zweiten Abbildung gegeben, ist die Funktion von x und y abhängig
nur von x abhängt. Ist jedoch der Kurvenverlauf aus der zweiten Abbildung gegeben, ist die Funktion von x und y abhängig 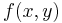 . Nun kann man aber nicht einfach nach
. Nun kann man aber nicht einfach nach 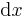 und
und 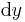 integrieren, weil man so eine Fläche aufspannen würde und so ein Flächenelement
integrieren, weil man so eine Fläche aufspannen würde und so ein Flächenelement 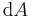 erhält. Deshalb wird in solchen Fällen das Wegelement
erhält. Deshalb wird in solchen Fällen das Wegelement 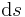 verwendet, weil es unabhängig von den jeweiligen Koordinaten ist. Das Wegelement
verwendet, weil es unabhängig von den jeweiligen Koordinaten ist. Das Wegelement 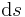 kann man sich als kleines Stück genau entlang des Weges vorstellen losgelöst von den jeweiligen Koordinatensystemen. Um solch einen komplizerten Weg konkret auszudrücken, gibt es mehrer Möglichkeiten. In dieser Vorlesung werden aber nur einfache Verläufe entlang der Koordinatenachsen uns bekannter Koordinatensysteme verwendet. Für kompliziertere Verläufe gibt es mathematische Hilfsmittel auf die hier aber nicht näher eingegangen werden soll. Es werden hauptsächlich für Wegelemente in den kartesischen Koordinaten
kann man sich als kleines Stück genau entlang des Weges vorstellen losgelöst von den jeweiligen Koordinatensystemen. Um solch einen komplizerten Weg konkret auszudrücken, gibt es mehrer Möglichkeiten. In dieser Vorlesung werden aber nur einfache Verläufe entlang der Koordinatenachsen uns bekannter Koordinatensysteme verwendet. Für kompliziertere Verläufe gibt es mathematische Hilfsmittel auf die hier aber nicht näher eingegangen werden soll. Es werden hauptsächlich für Wegelemente in den kartesischen Koordinaten 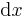 ,
,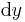 oder
oder 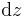 , in den Zylinderkoordinaten
, in den Zylinderkoordinaten 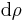 oder
oder 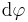 und in den Kugelkoordinaten
und in den Kugelkoordinaten 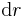 verwendet.
verwendet.
Um in den jeweiligen Integralen deutlich zu machen, dass man über einen Weg, eine Fläche oder ein Volumen integriert, wird an das Integral ein Differential 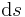 ,
,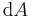 oder
oder 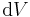 angehängt.
angehängt.
Vergleicht man nun aber das Differential einer Fläche oder eines Volumen mit dem Differential eines Weges, so ist deren Bedeutung etwas komplizierter zu fassen und auch die Transformation in verschiedene Koordinatensysteme ist nicht unbedingt trivial.
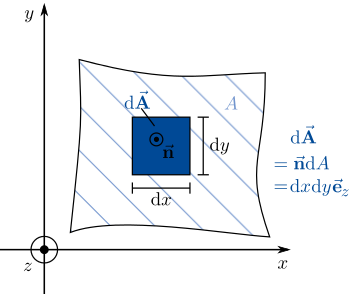
Im einfachsten Fall sind die zu bestimmenden Flächen- oder Volumenelemente in kartesischen Koordinaten gegeben. Zunächst ist hier eine Integrationsfläche zu sehen, die sich in x-und y-Richtung ausbreitet. Ein infinitesimales Teilstück dieser Fläche muss dem zufolge auch in beide Richtungen ausgedehnt sein, um die gesamte Fläche beschreiben zu können. Eine Integration über 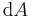 , kann dann auch als Integration über beide Wegelemente
, kann dann auch als Integration über beide Wegelemente 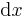 und
und 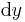 beschrieben werden, wie auch bei nicht infinitesimal kleinen Objekten die Fläche sich aus dem Produkt der Seiten x und y bestimmt.
beschrieben werden, wie auch bei nicht infinitesimal kleinen Objekten die Fläche sich aus dem Produkt der Seiten x und y bestimmt.
Bei Volumen ist es im Grunde dasselbe, es muss nur auch noch die Ausdehnung in z-Richtung berücksichtigt werden. Also ergibt sich ein infitesimales Volumenelement in kartesischen Koordinaten zu:
Schwieriger wird es, wenn die Wegelemente nicht mehr geradlinig verlaufen, dann müssen zur Berechnung der Flächen- und Volumenelemente so genannte Korrekturfaktoren eingeführt werden. Als Beispiel betrachtet man einen Kreisbogen in der x-y Ebene. Möchte man dort ein infinitesimales Flächenelement bestimmen so reicht es nicht aus einfach 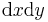 zu verwenden. Durch die Krümmung der Fläche würde der Fehler der dabei gemacht würde zu groß werden. Es bietet sich eine Koordinatentransformation in Polarkoordinaten an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden, und man macht keinen Fehler. Zur Bestimmung des Korrekturfaktors oder auch Metrikkoeffizienten betrachtet man nun ein Flächenelement des Kurvenstücks (vgl. Abbildung). Die Seitenlänge des Flächenelements entlang der r-Koordinate ist nicht gekrümmt und kann daher einfach als
zu verwenden. Durch die Krümmung der Fläche würde der Fehler der dabei gemacht würde zu groß werden. Es bietet sich eine Koordinatentransformation in Polarkoordinaten an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden, und man macht keinen Fehler. Zur Bestimmung des Korrekturfaktors oder auch Metrikkoeffizienten betrachtet man nun ein Flächenelement des Kurvenstücks (vgl. Abbildung). Die Seitenlänge des Flächenelements entlang der r-Koordinate ist nicht gekrümmt und kann daher einfach als 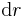 angenommen werden. Betrachtet man jedoch die
angenommen werden. Betrachtet man jedoch die  -Abhängigkeit so sieht man das die Krümmung des Kreisbogens nicht nur von
-Abhängigkeit so sieht man das die Krümmung des Kreisbogens nicht nur von  abhängt sondern auch von dem Radius r. Dies entspricht einer Umfangberechnung des Kreises. Der Gesamtumfang eines Kreises hat
abhängt sondern auch von dem Radius r. Dies entspricht einer Umfangberechnung des Kreises. Der Gesamtumfang eines Kreises hat 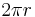 betrachtet man allerdings nur ein kleines Teilstück des Kreises folgt:
betrachtet man allerdings nur ein kleines Teilstück des Kreises folgt: 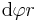 . Aus dieser Überlegung folgt, dass das infinitesimale Flächenelement einer Kreisfläche sich zu
. Aus dieser Überlegung folgt, dass das infinitesimale Flächenelement einer Kreisfläche sich zu 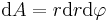 .
.
Aus ähnlichen Betrachtungen ergeben sich die Volumenelemente, die in den Abbildungen zu sehen sind:
Um das Volumenelement anzuwenden, betrachtet man zunächst in kartesischen Koordinaten eine Integration über ein Volumen. Dazu sei eine homogene Raumladung Um die Gesamtladung zu bestimmen, integriert man über das gesamte Volumen des Quaders: Da hier keine gekrümmten Flächen existieren, kann hier direkt das Volumenelement der kartesischen Koordinaten eingesetzt und das Integral gelöst werden: |
Im zweiten Beispiel soll eine Integration über ein Volumen in Kugelkoordinaten betrachtet werden. Dazu sei hier eine homogene Raumladung Dazu muss über das gesamte Volumen der Kugel integriert werden. Die Grenzen sind also die maximalen Ausdehnungen der Kugelkoordinaten, insbesondere für die Winkel Außerdem muss das Volumenelement in Kugelkoordinaten verwendet werden. Dies ergibt sich aus der Symmetrie, zu: Da aus der Abbildung folgt das für die Fläche eines infinitesimalen Stücks folgt, das nicht nur die Abhängigkeit in r-Richtung als auch die trigonometrischen Funktionen des Sinus und Cosinus folgen müssen. Eingesetzt folgt daraus: Da Dies enspricht abgesehen von der Konstante |
Multimediale Lehrmaterialien
|
http://highered.mcgraw-hill.com/sites/0073451342/student_view0/chapter13/section6/cylindrical_coordinates__app_.html Darstellung von infinitesimalen Volumenelementen in Zylinderkoordinaten (engl.) |
Hilfreiche Links
|
http://web.mit.edu/8.02t/www/materials/modules/ReviewB.pdf Bebilderte Erklärung zu Kartesischen-, Kugel-, und Zylinderkoordinatensystemen und deren infinitesimalen Elementen (engl.) |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Klaus Jänich Mathematik 1 Geschrieben für Physiker,2. Auflage (Springer Berlin Heidelberg, 2005)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Dr. Hempel, "Mathematische Grundlagen", Linienintegral, Universität Magdeburg
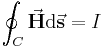
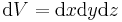


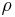 in einem Quader mit den Kantenlängen a, b und c gegeben.
in einem Quader mit den Kantenlängen a, b und c gegeben.
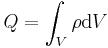
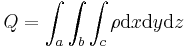
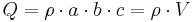
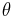 und
und