Vektorprodukt
| ← Zurück: Skalarprodukt | Übersicht: Vektorrechnung | Vorwärts: Komponentendarstellung von Vektoren → |
|
Zu diesem Thema stehen Aufgaben zur Selbstkontrolle zur Verfügung. |
Bei der Multiplikation zweier Vektoren handelt es sich entweder um das Vektorprodukt (auch Kreuzprodukt genannt) oder aber um das Skalarprodukt. Das Skalarprodukt liefert als Ergebnis ein Skalar, das Vektorprodukt hingegen liefert als Ergebnis wieder einen Vektor. Betrachtet man zwei Vektoren  und
und  , so erhält man als Ergebnis des Vektorprodukts einen Vektor
, so erhält man als Ergebnis des Vektorprodukts einen Vektor 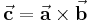 , der senkrecht auf der von
, der senkrecht auf der von  und
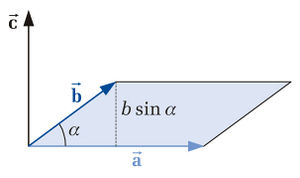
und  aufgespannten Fläche steht (siehe Abbildung). Weiterhin bilden die drei Vektoren
aufgespannten Fläche steht (siehe Abbildung). Weiterhin bilden die drei Vektoren  ,
,  und
und 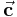 ein Rechtssystem, das heißt sie sind gemäß der Rechten-Hand-Regel II miteinander verknüpft. Der Betrag des Vektors
ein Rechtssystem, das heißt sie sind gemäß der Rechten-Hand-Regel II miteinander verknüpft. Der Betrag des Vektors 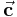 lässt sich als Flächeninhalt des von
lässt sich als Flächeninhalt des von  und
und  aufgespannten Parallelogramms interpretieren und wird wie folgt bestimmt:
aufgespannten Parallelogramms interpretieren und wird wie folgt bestimmt:
Dabei bezeichnet 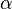 den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen
den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen 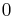 und
und 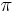 annehmen kann (siehe Abbildung). Weiterhin gilt es zu beachten, dass das Vektorprodukt ausschließlich für den dreidimensionalen euklidischen Vektorraum definiert ist. Rechnerisch gilt der folgende Zusammenhang:
annehmen kann (siehe Abbildung). Weiterhin gilt es zu beachten, dass das Vektorprodukt ausschließlich für den dreidimensionalen euklidischen Vektorraum definiert ist. Rechnerisch gilt der folgende Zusammenhang:
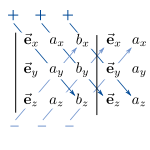
Als Merkhilfe für diesen Zusammenhang eignet sich die Regel von Sarrus: Entsprechend der Abbildung werden dabei die Einheitsvektoren des kartesischen Koordinatensystems in eine erste Spalte und die anderen beiden Vektoren in eine zweite und dritte Spalte geschrieben. Auf diese Weise erhält man eine Matrix, deren ersten beiden Spalten nun erneut rechts neben diese Matrix geschrieben werden. Nun führt man die Multiplikationen und Additionen wie in der Abbildung gezeigt aus und erhält:
Aus mathematischer Sicht bestimmt man auf diese Weise die Determinante der genannten Matrix. Anhand der beschriebenen Zusammenhänge zeigt sich, dass das Skalarprodukt nicht dem Kommutativgesetz genügt. Stattdessen gilt:
Weiterhin ergeben sich einige Sonderfälle, die im technischen Kontext häufig zu Vereinfachungen führen:
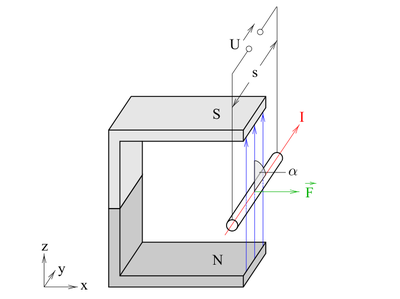
Betrachtet man einen vom Strom Gemäß der Rechten-Hand-Regel II zeigt die resultierende Kraft hier in Richtung Dabei bezeichnet |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/CrossProductOfVectorsInTheYZPlane/ Applet: Kreuzprodukt zweier Vektoren in der y-z-Ebene (engl.) |
Hilfreiche Links
|
http://www.mathe-online.at/materialien/Andreas.Pester/files/Vectors/kreuzprodukt.htm Bebilderte Erklärung zum Kreuzprodukt |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Wolfgang Pavel und Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
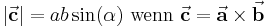
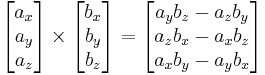
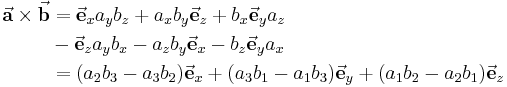
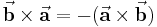
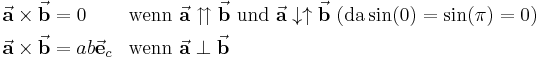
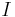 in Richtung
in Richtung 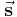 durchflossenen Leiter in einem homogenen magnetischen Feld
durchflossenen Leiter in einem homogenen magnetischen Feld 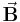 eines Hufeisenmagneten, so wird die wirkende Kraft
eines Hufeisenmagneten, so wird die wirkende Kraft 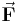 auf diesen Leiter durch das folgende Vektorprodukt beschrieben:
auf diesen Leiter durch das folgende Vektorprodukt beschrieben:
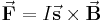
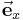 . Der Betrag der Kraft ergibt sich damit wie folgt:
. Der Betrag der Kraft ergibt sich damit wie folgt:
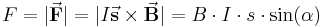
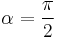 seinen maximalen Wert annimmt, ist die Kraftwirkung genau dann am größten, wenn das magnetische Feld und die Stromflussrichtung orthogonal zueinander gerichtet sind.
seinen maximalen Wert annimmt, ist die Kraftwirkung genau dann am größten, wenn das magnetische Feld und die Stromflussrichtung orthogonal zueinander gerichtet sind.

