| Der Vektor 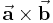 steht senkrecht auf der Fläche, die von den Vektoren steht senkrecht auf der Fläche, die von den Vektoren 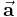 und und 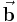 aufgespannt wird. aufgespannt wird. |
| Der Betrag des vektoriellen Produkts ist gleich der Fläche des Parallelogramms, das von 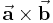 aufgespannt wird. aufgespannt wird. |
| → | Da die Formel des Vektorprodukts nicht nur das vektorielle Produkt, sondern auch den Sinus des eingeschlossenen Winkels enthält, ist diese Antwort falsch. Weitere Erklärung siehe Rechte Hand Regel 1 |
| Die Vektoren 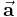 , , 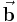 und und 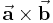 bilden ein Rechtssystem, das heißt, sie sind angeordnet wie Daumen, Mittelfinger und Zeigefinger der rechten Hand. bilden ein Rechtssystem, das heißt, sie sind angeordnet wie Daumen, Mittelfinger und Zeigefinger der rechten Hand. |