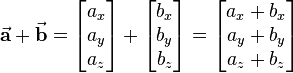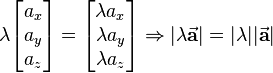Difference between revisions of "Simple arithmetic operations"

From Robotics
Jump to: navigation, search
Line 2: Line 2:
  
 
===Addition and subtraction of vectors===
 
===Addition and subtraction of vectors===
−
[[File:vectoralgebra_addition_substraction.png|right|280px]]
+
[[File:vectoralgebra_addition_substraction.png|right|400px]]
  
 
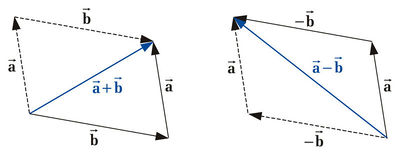
Vectors can be added graphically as well as computationally. Using the graphical method, one of the vectors is shifted such that its startpoint is positioned at the endpoint of the other vector. The resulting vector is called sum vector. It starts at the startpoint the one vector and ends at the endpoint of the shifted vector (see figure on the right). At the computational addition the single components are added
 
Vectors can be added graphically as well as computationally. Using the graphical method, one of the vectors is shifted such that its startpoint is positioned at the endpoint of the other vector. The resulting vector is called sum vector. It starts at the startpoint the one vector and ends at the endpoint of the shifted vector (see figure on the right). At the computational addition the single components are added
Line 25: Line 25:
  
 
===Multiplication of vectors with scalars===
 
===Multiplication of vectors with scalars===
−
[[File:vectoralgebra_multiplication_scalar.png|right|350px]]
+
[[File:vectoralgebra_multiplication_scalar.png|right|280px]]
 
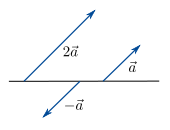
The multiplication of a vector <math>\vec{\textbf{a}}</math> with a positive real scalar <math>\lambda</math> results in a new vector whose direction suits the direction of the initial vector. A negative <math>\lambda</math> leads to a vector with opposite direction. In both cases the length of the new vector changes with the factor <math>|\lambda|</math>. This is obvious because each component of the vector is multiplied with the scalar:
 
The multiplication of a vector <math>\vec{\textbf{a}}</math> with a positive real scalar <math>\lambda</math> results in a new vector whose direction suits the direction of the initial vector. A negative <math>\lambda</math> leads to a vector with opposite direction. In both cases the length of the new vector changes with the factor <math>|\lambda|</math>. This is obvious because each component of the vector is multiplied with the scalar:
 
:<math>
 
:<math>

Revision as of 11:27, 15 May 2014

← Back: Unit vectors Overview: Vector algebra Next: Dot product →

Addition and subtraction of vectors

Vectoralgebra addition substraction.png

Vectors can be added graphically as well as computationally. Using the graphical method, one of the vectors is shifted such that its startpoint is positioned at the endpoint of the other vector. The resulting vector is called sum vector. It starts at the startpoint the one vector and ends at the endpoint of the shifted vector (see figure on the right). At the computational addition the single components are added

\vec{\mathbf{a}} + \vec{\mathbf{b}} = \begin{bmatrix} a_x\\a_y\\a_z \end{bmatrix} + \begin{bmatrix} b_x\\b_y\\b_z \end{bmatrix} = \begin{bmatrix} a_x+b_x\\a_y+b_y\\a_z+b_z \end{bmatrix}

Both the graphical and the computational addition show, that the commutative law holds:

\vec{\mathbf{a}}+\vec{\mathbf{b}} = \vec{\mathbf{b}}+\vec{\mathbf{a}}

The resulting vector of the substraction of vectors is called difference vector. Because it holds that 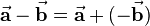\vec{\mathbf{a}}-\vec{\mathbf{b}} = \vec{\mathbf{a}}+(-\vec{\mathbf{b}}) the two vectors can just be added after inverting the direction of the second vector (see figure on the right). For the computational method the components are substracted:

\vec{\mathbf{a}} - \vec{\mathbf{b}} = \begin{bmatrix} a_x\\a_y\\a_z \end{bmatrix} - \begin{bmatrix} b_x\\b_y\\b_z \end{bmatrix} = \begin{bmatrix} a_x-b_x\\a_y-b_y\\a_z-b_z \end{bmatrix}

If more than two vectors are added or substracted the same relations hold. Using the graphical method for example, all the vectors are stringed together.

Multiplication of vectors with scalars

Vectoralgebra multiplication scalar.png

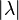The multiplication of a vector \vec{\textbf{a}} with a positive real scalar \lambda results in a new vector whose direction suits the direction of the initial vector. A negative \lambda leads to a vector with opposite direction. In both cases the length of the new vector changes with the factor |\lambda|. This is obvious because each component of the vector is multiplied with the scalar:

\lambda \begin{bmatrix} a_x\\a_y\\a_z \end{bmatrix} = \begin{bmatrix} \lambda a_x\\ \lambda a_y\\ \lambda a_z \end{bmatrix} \Rightarrow |\lambda \vec{\textbf{a}}| = |\lambda| |\vec{\textbf{a}}|

Multiplication with a scalar 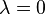\lambda = 0 results in the zero vector 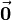\vec{\mathbf{0}} with magnitude 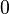0 and undefined direction.

Multimedial educational material

Multimedia.png

http://mathcasts.org/gg/student/matrices/vectors_adding/index_s.html Applet: Vector addition in cartesian coordinates

http://demonstrations.wolfram.com/VectorsIn3D/ Applet: Vector addition in three-dimensional space (free CDF-Player of Wolfram required)

http://demonstrations.wolfram.com/3DVectorDecomposition/ Applet: Vector addition in in three-dimensional space with three vectors (free CDF-Player required)

http://www.math.ethz.ch/~lemuren/public/visualization/analysis/RealComputation.html Applet: Vector addition in two-dimensional space

http://demonstrations.wolfram.com/SumOfTwoVectors/ Applet: Vector addition in cartesian coordinates (free CDF-Player of Wolfram required)

Helpful links

Link.png

http://hyperphysics.phy-astr.gsu.edu/hbase/vect.html General introduction to vector operations

Literature

  • Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Edition (Pearson Studium, 2011)
Retrieved from "https://getwww.uni-paderborn.de/wiki/robotics/index.php?title=Simple_arithmetic_operations&oldid=229"