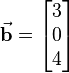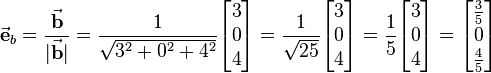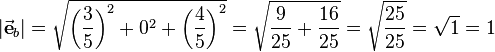Unit vectors
| ← Back: Vector algebra | Overview: Vector algebra | Next: Simple arithmetic operations → |
|
|
A unit vector is a vector with magnitude 1. The unit vector to a given vector 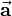 can be determined by dividing the given vector by its magnitude
can be determined by dividing the given vector by its magnitude 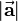 :
:
The vector 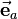 has the magnitude 1 (so
has the magnitude 1 (so 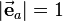 ) and is pointed to the direction of
) and is pointed to the direction of 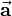 . So every vector can be described by its magnitude (so a scalar value) and the corresponding unit vector. Therefore
. So every vector can be described by its magnitude (so a scalar value) and the corresponding unit vector. Therefore 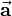 can also be written as follows:
can also be written as follows:
How arithmetic operations like fractions are handled exactly, is described in the article about simple arithmetic operations.
Hint: For detailed information about the handling of arithmetic operations please have a look on the article about simple arithmetic operations To the given vector The calculation of the magnitude shows thats it equals 1 indeed: |
Literature
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Edition (Pearson Studium, 2011)
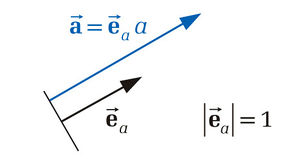
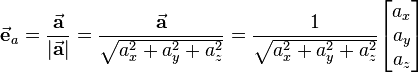
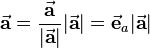
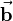 the corresponding unit vector shall be determined:
the corresponding unit vector shall be determined: