Difference between revisions of "Rotations using quaternions"
From Robotics
| Line 2: | Line 2: | ||
[[File:quaternion-rpy.png|right|350px]] | [[File:quaternion-rpy.png|right|350px]] | ||
| − | Usually rotations are defined by 3 angles, either [[Euler angles|Euler]] or [[Roll-Pitch-Yaw]] angles. So three successive rotations around three different axes lead to a combined rotation, that can be described by a single rotation matrix. Such a combined rotation is equal to a rotation around a certain axis in three-dimensional space about a certain angle. This is shown in the figure on the right. | + | Usually rotations are defined by 3 angles, either [[Euler angles|Euler]] or [[Roll-Pitch-Yaw]] angles. So three successive rotations around three different axes lead to a combined rotation, that can be described by a single rotation matrix. Such a combined rotation is equal to a rotation around a certain axis in three-dimensional space about a certain angle. This is shown in the figure on the right. The vector <math>\vec{\mathbf{r}}</math> is rotated such that it results in <math>\vec{\mathbf{r}}'</math>. This could be done by rotating the vector around the z-, the y- and the x-axis successively or by just rotating it around the rotation axis <math>\vec{\mathbf{u}}</math> by <math>\phi</math>. The result is the same. |
Revision as of 14:34, 2 September 2015
| ← Back: Multiplication of quaternions | Overview: Quaternions | Next: Realization of transformations → |
Usually rotations are defined by 3 angles, either Euler or Roll-Pitch-Yaw angles. So three successive rotations around three different axes lead to a combined rotation, that can be described by a single rotation matrix. Such a combined rotation is equal to a rotation around a certain axis in three-dimensional space about a certain angle. This is shown in the figure on the right. The vector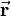 
is rotated such that it results in 
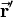. This could be done by rotating the vector around the z-, the y- and the x-axis successively or by just rotating it around the rotation axis 
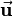by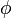 
. The result is the same.
