Euler angles

← Back: Roll-Pitch-Yaw

Overview: Three-Angle Representations

Next: Quaternions →

The Euler angles are three angles defined in regard of relative transformation to describe the orientation of an object in three-dimensional space. So unlike the roll, pitch and yaw angles which are applied to static axes, Euler angles are always applied to the new coordinate axes.

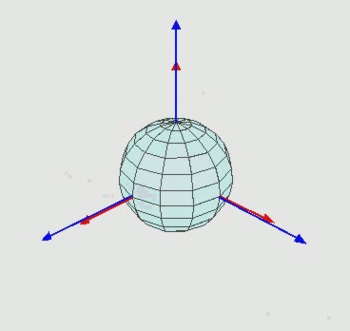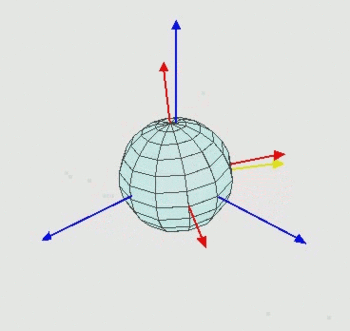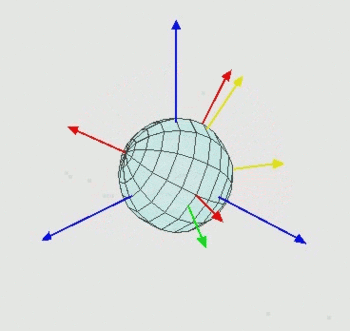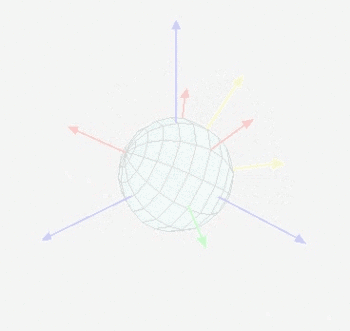
There are different conventions for Euler angles which differ in the definition of the three rotation axes. Two pure Euler conventions are ZXZ and ZYZ. In the ZXZ convention the first rotation is around the z-axis, then a rotation around the new x-axis follows and another rotation around the current z-axis. The ZYZ convention implies, as the name already says, a rotation around the z-axis, then a rotation around the new y-axis followed by a rotation around the new z-axis. An example is shown in the figure on the right side.

So the ZYZ transformation matrix of the orientation is defined as follows:

$\begin{align} Euler(\phi,\theta,\psi)&=Rot(z,\phi)Rot(y,\theta)Rot(z,\psi) \\ &= \left[\begin{array}{cccc} \cos{\phi}\cos{\psi}\cos{\theta}-\sin{\phi}\sin{\psi} & -\cos{\phi}\sin{\psi}-\cos{\psi}\cos{\theta}\sin{\phi} & \cos{\psi}\sin{\theta} & 0\\ \cos{\psi}\sin{\phi}+\cos{\phi}\sin{\psi} & \cos{\phi}\cos{\psi}-\cos{\theta}\sin{\phi}\sin{\psi} & \sin{\psi}sin{\theta} & 0\\ -\cos{\phi}\sin{\theta} & \sin{\phi}\sin{\theta} & \cos{\theta} & 0\\ 0 & 0 & 0 & 1 \end{array}\right] \end{align}$

The following video shows an example for the ZXZ convention. It can be seen, how the object is rotated successively around the three axes: