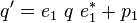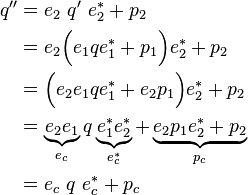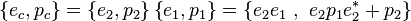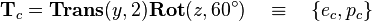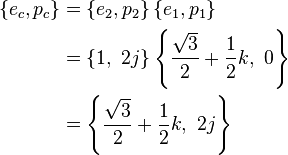Difference between revisions of "Realization of transformations"
| (42 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{Navigation|before=[[Composition of rotations]]|overview=[[Quaternions]]|next=[[ | + | {{Navigation|before=[[Composition of rotations]]|overview=[[Quaternions]]|next=[[Denavit-Hartenberg Convention]]}} |
===Quaternion notation for general transformations=== | ===Quaternion notation for general transformations=== | ||
| Line 14: | Line 14: | ||
q' = e\ q\ e^*+ p | q' = e\ q\ e^*+ p | ||
</math> | </math> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Assume a pure translation is to be described using the above notation. Thus the rotation quaternion <math>e_t</math> of a pure translation describes a rotation with an angle <math>\phi=0^\circ</math> which is actually no rotation at all. According to [[Rotations using quaternions]] <math>e</math> is defined as: | ||
| + | :<math> | ||
| + | e_t(\vec{\mathbf{u}},0^\circ)=\cos{0^\circ} + \sin{0^ \circ}\vec{\mathbf{u}} = 1+0\cdot\vec{\mathbf{u}} = 1 | ||
| + | </math> | ||
| + | The rotation axis <math>\vec{\mathbf{u}}</math> can be any arbitrary unit vector as the sine of <math>0^\circ</math> is zero. So <math>e_t</math> of a pure translation is always just <math>1</math>. | ||
| + | |||
| + | The translation quaternion <math>p_t</math> of a pure translation has the scalar part <math>0</math> and the translation vector <math>\vec{\mathbf{p}}</math> as vector part: | ||
| + | :<math> | ||
| + | p_t=0\oplus\left[\begin{array}{c}p_x\\p_y\\p_z\end{array}\right] = p_xi+p_yj+p_zk | ||
| + | </math> | ||
| + | So a pure translation by vector <math>[p_x\ p_y\ p_z]^T</math> is defined as: | ||
| + | :<math> | ||
| + | \left\{e_t,p_t\right\}=\left\{1,\ p_xi+p_yj+p_zk\right\} | ||
| + | </math> | ||
| + | |||
| + | {{Example | ||
| + | |Title=Translation | ||
| + | |Contents= | ||
| + | A translation by <math>2</math> on the <math>y</math>-axis for example would be | ||
| + | :<math> | ||
| + | \mathbf{Trans}(y,2) \equiv \left\{1,\ 2j\right\} | ||
| + | </math> | ||
| + | }} | ||
| + | |||
| + | ---- | ||
| + | |||
| + | For a pure rotation there is no translation. Thus the translation quaternion <math>p_r</math> of a pure rotation is a zero quaternion: | ||
| + | :<math> | ||
| + | p_r=0 \oplus \left[\begin{array}{c}0\\0\\0\end{array}\right] = 0 | ||
| + | </math> | ||
| + | The rotation quaternion <math>e_r</math> of a pure rotation around an axis defined by a unit vector <math>\vec{\mathbf{u}}</math> by the angle <math>\phi</math> is: | ||
| + | :<math> | ||
| + | e_r(\vec{\mathbf{u}},\phi)=\cos{\frac{\phi}{2}} + \sin{\frac{\phi}{2}}\vec{\mathbf{u}} | ||
| + | </math> | ||
| + | So a pure rotation is defined as: | ||
| + | :<math> | ||
| + | \left\{e_r,p_r\right\}=\left\{\cos{\frac{\phi}{2}} + \sin{\frac{\phi}{2}}\vec{\mathbf{u}},\ 0\right\} | ||
| + | </math> | ||
| + | |||
| + | {{Example | ||
| + | |Title=Rotation | ||
| + | |Contents= | ||
| + | A rotation by <math>60^\circ</math> around the <math>z</math>-axis for example would be | ||
| + | :<math> | ||
| + | \mathbf{Rot}(z,60^\circ) \equiv \left\{\cos{30^\circ} + \sin{30^\circ}\left[\begin{array}{c}0\\0\\1\end{array}\right],\ 0\right\} = \left\{\frac{\sqrt{3}}{2} + \frac{1}{2}k,\ 0\right\} | ||
| + | </math> | ||
| + | }} | ||
===Combination of transformations=== | ===Combination of transformations=== | ||
| Line 28: | Line 78: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | But how can the two quaternions <math>e_c</math> and <math>p_c</math> of the quaternion notation be calculated based on the quaternions of individual transformations? The first transformation leads to | + | But how can the two quaternions <math>e_c</math> and <math>p_c</math> of the quaternion notation be calculated based on the quaternions of the individual transformations? The first transformation leads to |
:<math> | :<math> | ||
q' = e_1\ q\ e_1^*+ p_1 | q' = e_1\ q\ e_1^*+ p_1 | ||
</math> | </math> | ||
| − | Now the second transformation is applied on <math>q'</math>: | + | Now the second transformation is applied on <math>q'</math>. The resulting equation can be solved using the [[Multiplication of quaternions|distributive law for quaternions]] to determine <math>e_c</math> and <math>p_c</math>: |
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
q'' &= e_2\ q'\ e_2^*+ p_2 \\ | q'' &= e_2\ q'\ e_2^*+ p_2 \\ | ||
| − | &= e_2\Big(e_1\ q\ | + | &= e_2\Big(e_1qe_1^*+ p_1\Big)e_2^*+ p_2 \\ |
| + | &= \Big(e_2e_1qe_1^*+ e_2p_1\Big)e_2^*+ p_2 \\ | ||
| + | &= \underbrace{e_2e_1}_{e_c}q\underbrace{e_1^*e_2^*}_{e_c^*}+\underbrace{e_2p_1e_2^*+ p_2}_{p_c} \\ | ||
| + | &= e_c\ q\ e_c^*+p_c \\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | Thus the combination of two transformations can be denoted in quaternion notation as | ||
| + | :<math> | ||
| + | \left\{e_c,p_c\right\}=\left\{e_2,p_2\right\}\left\{e_1,p_1\right\}=\left\{e_2e_1\ , \ e_2p_1e_2^*+p_2\right\} | ||
| + | </math> | ||
| + | Using the knowledge about [[Addition of quaternions|addition of quaternions]] and [[Rotations using quaternions|rotations]] and [[Composition of rotations|composition of rotations]] using quaternions this can directly be determined regarding the homogeneous transformation matrix <math>\mathbf{T}_c</math> and its rotational and translational components <math>\mathbf{R}_c</math> and <math>\vec{\mathbf{p}}_c</math>. | ||
| + | |||
| + | {{Example | ||
| + | |Title=Combination of rotation and translation | ||
| + | |Contents= | ||
| + | The two examples for rotation and rotation are now to be combined. The combined transform is defined as: | ||
| + | :<math> | ||
| + | \mathbf{T}_c = \mathbf{Trans}(y,2)\mathbf{Rot}(z,60^\circ) \quad \equiv \quad \left\{e_c,p_c\right\} | ||
| + | </math> | ||
| + | Using the explanations above this leads to: | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | \left\{e_c,p_c\right\}&=\left\{e_2,p_2\right\}\left\{e_1,p_1\right\}\\ | ||
| + | &= \left\{1,\ 2j\right\}\left\{\frac{\sqrt{3}}{2} + \frac{1}{2}k,\ 0\right\}\\ | ||
| + | &= \left\{\frac{\sqrt{3}}{2} + \frac{1}{2}k,\ 2j\right\} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| + | }} | ||
| + | |||
| + | [[Category:Article]] | ||
| + | [[Category:Quaternion]] | ||
Latest revision as of 18:18, 13 November 2015
| ← Back: Composition of rotations | Overview: Quaternions | Next: Denavit-Hartenberg Convention → |
Quaternion notation for general transformations
Up to now transformations have been defined by homogeneous matrices combining a rotation matrix 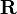 and a translation vector
and a translation vector 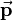 . Now a new notation is introduced to represent a transformation using two quaternions
. Now a new notation is introduced to represent a transformation using two quaternions  and
and 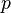 :
:
The quaternion  is equivalent to
is equivalent to 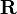 and describes the rotation while
and describes the rotation while 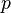 is defined as
is defined as 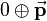 and so equivalent to the translation.
and so equivalent to the translation.
Applying such a transformation to a quaternion 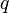 is done by first rotating
is done by first rotating 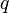 with
with  corresponding to the rotation equation and then adding
corresponding to the rotation equation and then adding 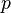 :
:
Assume a pure translation is to be described using the above notation. Thus the rotation quaternion 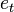 of a pure translation describes a rotation with an angle
of a pure translation describes a rotation with an angle 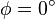 which is actually no rotation at all. According to Rotations using quaternions
which is actually no rotation at all. According to Rotations using quaternions  is defined as:
is defined as:
The rotation axis 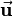 can be any arbitrary unit vector as the sine of
can be any arbitrary unit vector as the sine of 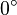 is zero. So
is zero. So 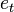 of a pure translation is always just
of a pure translation is always just 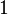 .
.
The translation quaternion 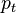 of a pure translation has the scalar part
of a pure translation has the scalar part 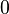 and the translation vector
and the translation vector 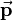 as vector part:
as vector part:
So a pure translation by vector ![[p_x\ p_y\ p_z]^T](/wiki/robotics/images/math/b/d/7/bd718cfcc5455c1753dfc9a0abb34e82.png) is defined as:
is defined as:
A translation by |
For a pure rotation there is no translation. Thus the translation quaternion 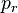 of a pure rotation is a zero quaternion:
of a pure rotation is a zero quaternion:
The rotation quaternion 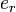 of a pure rotation around an axis defined by a unit vector
of a pure rotation around an axis defined by a unit vector 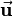 by the angle
by the angle 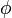 is:
is:
So a pure rotation is defined as:
A rotation by |
Combination of transformations
It is known that a combination of transformations is defined as:
But how can the two quaternions 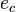 and
and 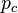 of the quaternion notation be calculated based on the quaternions of the individual transformations? The first transformation leads to
of the quaternion notation be calculated based on the quaternions of the individual transformations? The first transformation leads to
Now the second transformation is applied on 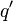 . The resulting equation can be solved using the distributive law for quaternions to determine
. The resulting equation can be solved using the distributive law for quaternions to determine 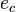 and
and 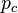 :
:
Thus the combination of two transformations can be denoted in quaternion notation as
Using the knowledge about addition of quaternions and rotations and composition of rotations using quaternions this can directly be determined regarding the homogeneous transformation matrix 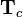 and its rotational and translational components
and its rotational and translational components 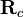 and
and 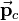 .
.
The two examples for rotation and rotation are now to be combined. The combined transform is defined as: Using the explanations above this leads to: |
![\mathbf{T} = \left[\begin{array}{cccc} & & & \\ & \mathbf{R} & & \vec{\mathbf{p}} \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right] \quad \equiv \quad \left\{e,p\right\}](/wiki/robotics/images/math/6/6/1/661d04cca4174d58de7984920f826fb3.png)

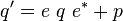
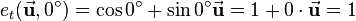
![p_t=0\oplus\left[\begin{array}{c}p_x\\p_y\\p_z\end{array}\right] = p_xi+p_yj+p_zk](/wiki/robotics/images/math/f/d/3/fd3d3f36de984a1b7147c5b64f3c2967.png)
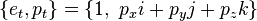
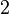 on the
on the 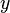 -axis for example would be
-axis for example would be
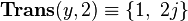
![p_r=0 \oplus \left[\begin{array}{c}0\\0\\0\end{array}\right] = 0](/wiki/robotics/images/math/9/e/f/9ef8f9de5598344b48857003e47bf592.png)
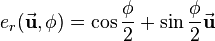
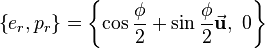
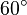 around the
around the 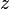 -axis for example would be
-axis for example would be
![\mathbf{Rot}(z,60^\circ) \equiv \left\{\cos{30^\circ} + \sin{30^\circ}\left[\begin{array}{c}0\\0\\1\end{array}\right],\ 0\right\} = \left\{\frac{\sqrt{3}}{2} + \frac{1}{2}k,\ 0\right\}](/wiki/robotics/images/math/f/a/5/fa5a969f8321beb3e917c8de24c6e5d1.png)
![\begin{align}
\mathbf{T}_c = \mathbf{T}_2\mathbf{T}_1 =
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_2\mathbf{R}_1 & & \vec{\mathbf{p}}_2+\mathbf{R}_2\vec{\mathbf{p}}_1 \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
=
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_c & & \vec{\mathbf{p}}_c \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
\quad \equiv \quad
\left\{e_c,p_c\right\}=\left\{e_2,p_2\right\}\left\{e_1,p_1\right\}
\end{align}](/wiki/robotics/images/math/8/b/c/8bc75145f54c5ab026e992e40f2a1842.png)